この記事のコードをまとめたものはGithubにあります。
使用するパッケージ
# 使用するパッケージ
library(tidyverse)
library(magrittr)
library(broom)
library(stargazer)
library(car)
library(QuantPsyc)
# ggplot2 の theme をあらかじめ設定しておく
theme_set(theme_minimal(base_size = 15))
使用するデータ
data <- read_csv("Data/House_of_Councilors_1996_2017.csv") # 1996年~2017年に行われた衆院選の選挙データ
data %<>%
filter(year == 2005) %>% # 2005年のデータに絞る
filter(party_jpn %in% c("自民党", "民主党", "共産党")) %>% # 簡単のため、候補者の数が多い政党に絞る
as.data.frame() %>%
drop_na() # 欠損値を除外する
分析をする流れ
- 分析の目的を設定する
- 理論と仮説
- 変数選択
3-1.従属変数を設定
3-2. 独立変数の設定
3-3. 統制変数の選別 - データの可視化
4-1. 従属変数のヒストグラムを確認
4-2. 従属変数と独立変数の散布図を確認 - 重回帰分析
5-1. 重回帰分析の実行
5-2. モデルの診断
5-3. 点・区間推定の可視化
5-4. 得票率の予測値 - 分析結果の解釈
1. 分析の目的を設定する
何をするにしても目的が設定されていなければ、何もできない。
「どのような疑問を有しているのか」や「何が知りたいのか」が定まっていなければ、
インドに旅行して「自分探し」をするなどの間違ったアプローチをしかねないのだ。
「どのような疑問を有しているのか」や「何が知りたいのか」をアカデミックの世界では「リサーチクエスチョン」という。
まずは、この「リサーチクエスチョン」を設定しよう。
今回は選挙研究を事例に重回帰分析の流れを紹介する。
そのうえで、「候補者は選挙に金をかければ、票を得られるのか」というリサーチクエスチョンを立てた。
2. 理論と仮説
変数選択をする際は、リサーチクエスチョンからどのような理論を立てられるのか。
そして、この理論を実証するには、どのような仮説を立てて検証するべきかを考える必要がある。
理論:
選挙に金をかけると、「スタッフの増員」・「選挙カーの使用」などが可能になり、票を集めやすくなる
上記の理論が正しければ、以下のような仮説が立てられる。
仮説:
選挙費用が多ければ多いほど、得票率が高い
3. 変数選択
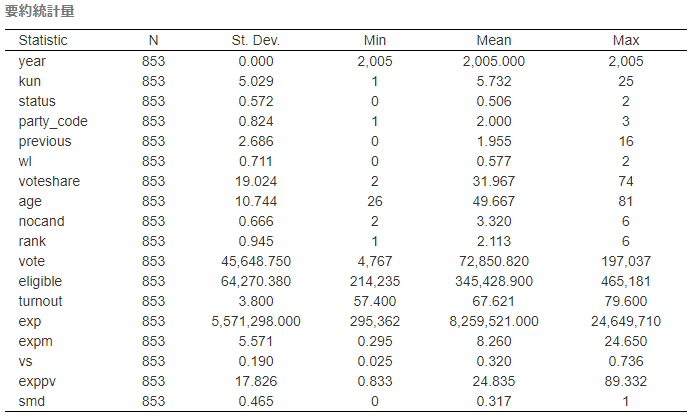
# 要約統計量をHTMLで出力する。
# チャンクオプションにresults='asis'を忘れないように
data %>%
stargazer(type = "html",
summary.stat = c("n", "sd", "min", "mean", "max"),
title = "要約統計量",
align = T)
| 変数名 | 内容 | 備考 |
|---|---|---|
| year | 実施年 | |
| ku | 都道府県 | |
| kun | 区域 | |
| status | 現職か否か | 0 = 新人・元, 1 = 現職 |
| name | 名前 | |
| party | 所属政党 | ローマ字での略語 |
| party_code | 所属政党 | 数字で通し番号 |
| previous | 当選回数 | |
| wl | 当落結果 | 0 = 落選, 1 = 当選, 2 = 復活当選 |
| voteshare | 得票率 | 単位: % |
| age | 年齢 | |
| nocand | 候補者数 | |
| rank | 順位 | |
| vote | 得票数 | |
| eligible | 有権者数 | |
| turnout | 投票率 | 単位: % |
| exp | 選挙費用 | 単位: 円 |
| expm | 選挙費用 | 単位: 百万円 |
| vs | 得票割合 | 小数で表記 |
| exppv | 選挙費用 | 単位: 円(有権者一人当たりの選挙費用) |
| smd | 当落 | 0 = 落選, 1 = 当選 |
| party_jpn | 所属政党 | 日本語 |
3-1. 従属変数の選択
従属変数: voteshare(得票率)
これは考える余地なし。
仕事でデータ分析をする場合、すんなり従属変数が決まるとは限らない。
3-2. 独立変数の選別
独立変数: exppv(有権者一人当たりの選挙費用)
これも選挙費用で考える余地なし。
問題はどのように選挙費用を加工するかだ。
有権者数一人当たりの選挙費用が妥当と考えた理由は、選挙運動をする区域や自治体の規模で最低限必要になる選挙費用は異なるからだ。
3-3. 統制変数の選別
統制変数1: previous(当選回数)
当選回数は選挙の強さに近似すると考えられるため。
統制変数2: nocand(候補者数)
候補者数が増えると票が分散するため、得票率に影響を与えると考えられるため。
統制変数3: 政党規模(自民党・民主党ダミー)
自民大国や民主大国という言葉があるように、自民党や民主党は日本の大政党である。
大政党には知名度や組織力、多額の寄付金があり、票が集まりやすい傾向があると考えられる。
つまり、自民党・民主党と共産党で切片が異なるということだ。そのため、このダミー変数が必要だろう。
# 政党規模ダミーの作成
data %<>%
mutate("party_size" = if_else(party_jpn %in% c("自民党", "民主党"), 1, 0))
# 0 = 共産党
# 1 = 自民党・民主党
4. データの可視化
4-1. 従属変数のヒストグラムを確認
data %>%
ggplot(aes(x = voteshare)) +
geom_histogram(aes(y = ..density..), color = "black", fill = "gray") +
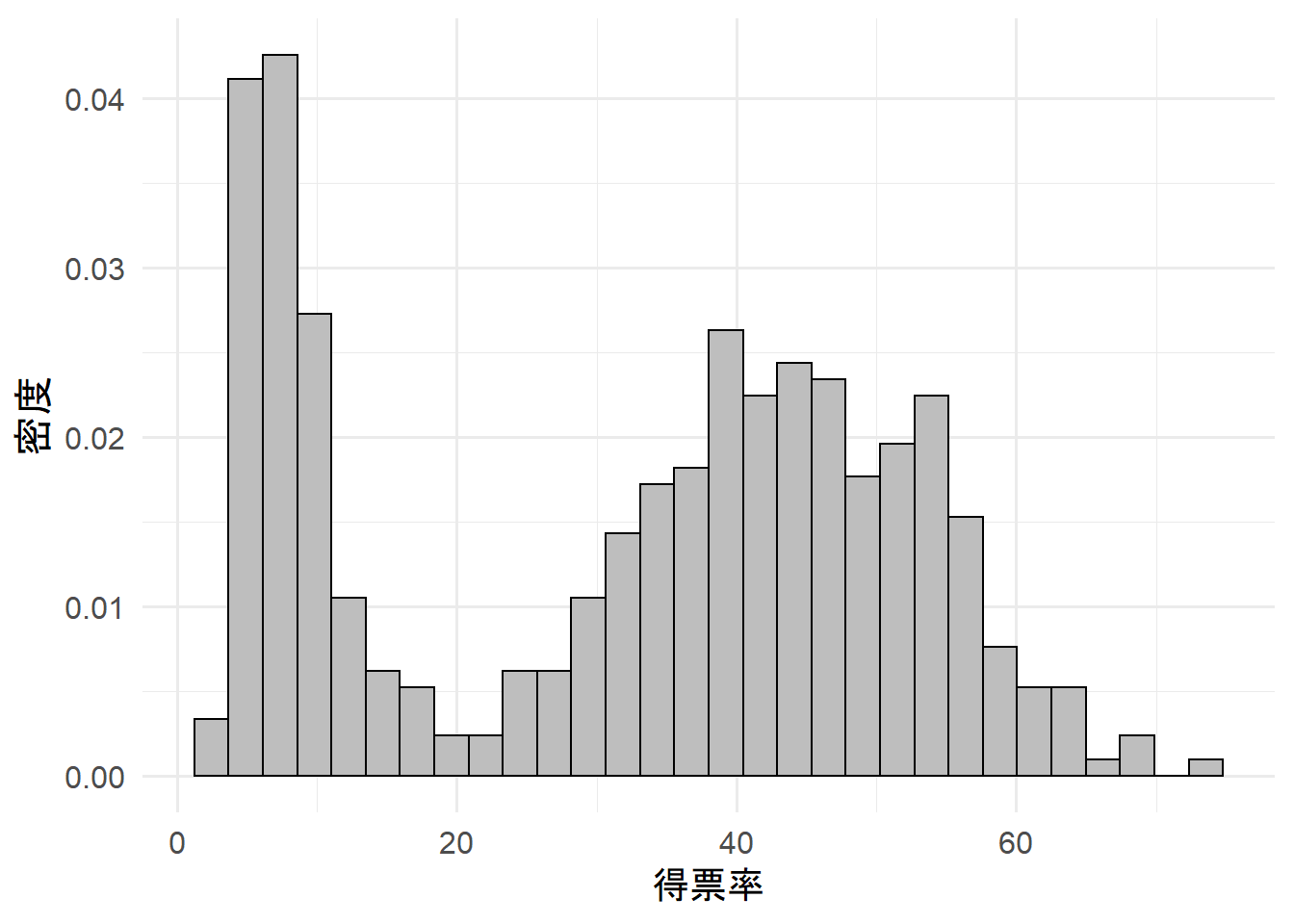
labs(x = "得票率", y = "密度")
2つのピークが見られる。これは従属変数に2つのクラスタが存在することを示唆している。
おそらく、政党規模で層化すると原因が分かると思う。
data %>%
ggplot(aes(x = voteshare)) +
geom_histogram(aes(y = ..density..),
color = "black",
fill = "gray") +
labs(x = "得票率",
y = "密度") +
facet_wrap(~ party_size,
labeller = as_labeller(c(`0` = "共産党",
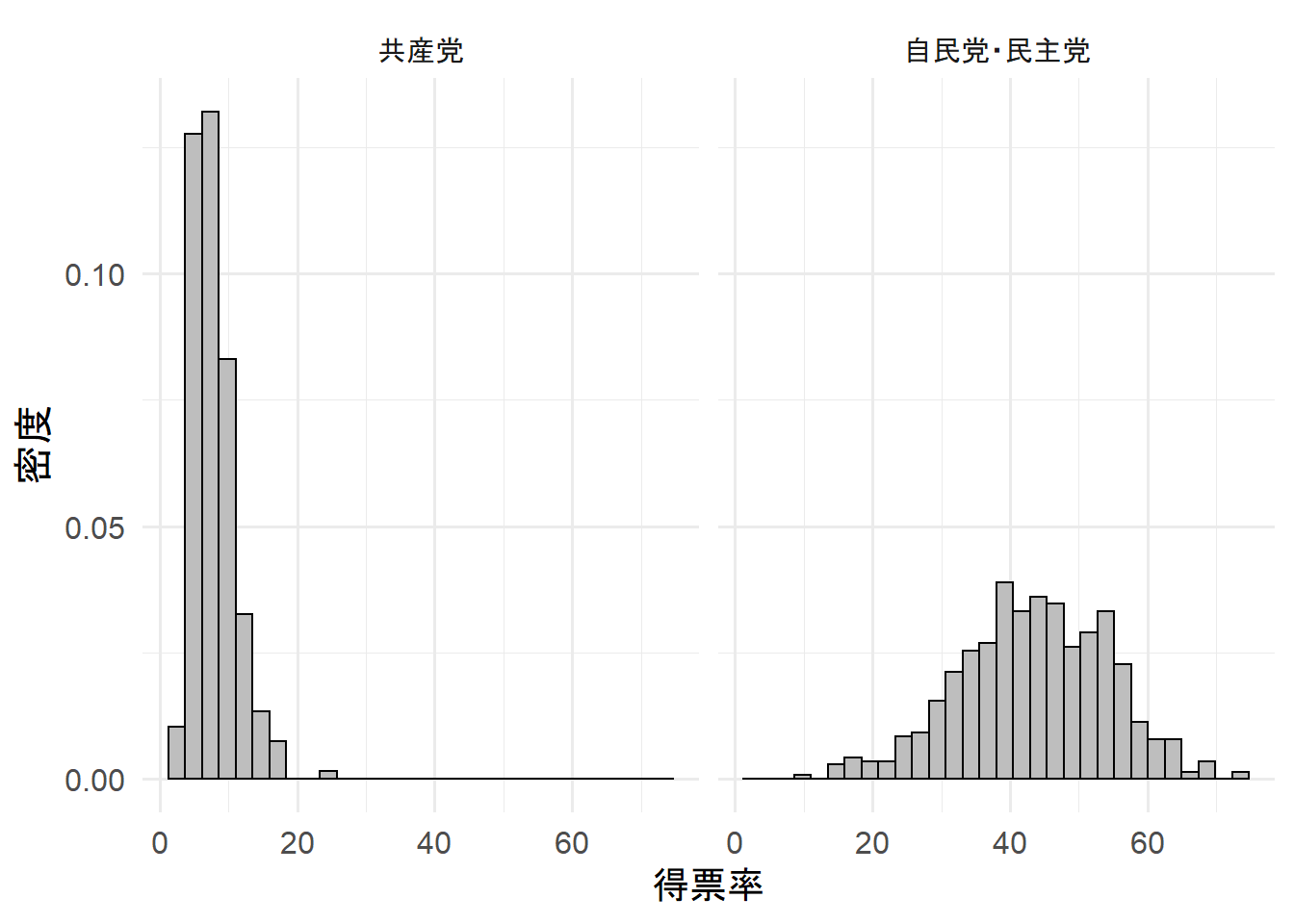
`1` = "自民党・民主党")))
実際に層化してみた。
やはり、自民党・民主党クラスタと共産党クラスタがあるようだ。
このことから、政党規模ダミーを統制変数として投入する必要性が確かなものになった。
4-2. 従属変数と独立変数の散布図を確認
data %>%
ggplot(aes(x = exppv,
y = voteshare,
color = factor(party_size))) +
geom_point() +
geom_smooth(method = lm) +
scale_color_discrete(name = "政党規模",
breaks = c("0", "1"),
labels = c("共産党", "自民党・民主党")) +
labs(x = "有権者一人当たりの選挙費用",
y = "得票率",
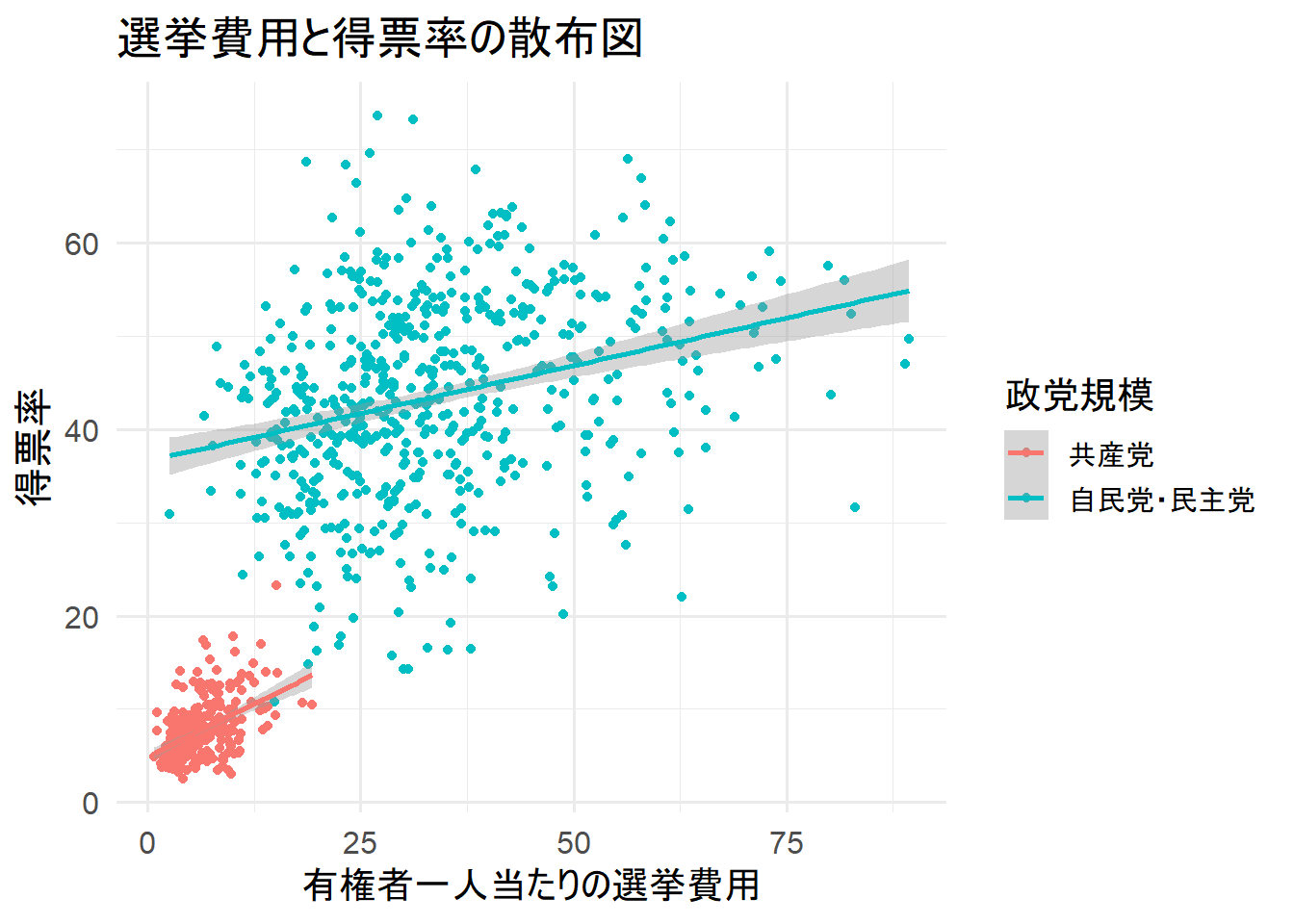
title = "選挙費用と得票率の散布図")
正の相関が見られる。
回帰直線が外れ値に引っ張られている様子は見えない。
data %>%
ggplot(aes(x = previous,
y = voteshare,
color = factor(party_size))) +
geom_point() +
geom_smooth(method = lm) +
scale_color_discrete(name = "政党規模",
breaks = c("0", "1"),
labels = c("共産党", "自民党・民主党")) +
labs(x = "当選回数",
y = "得票率",
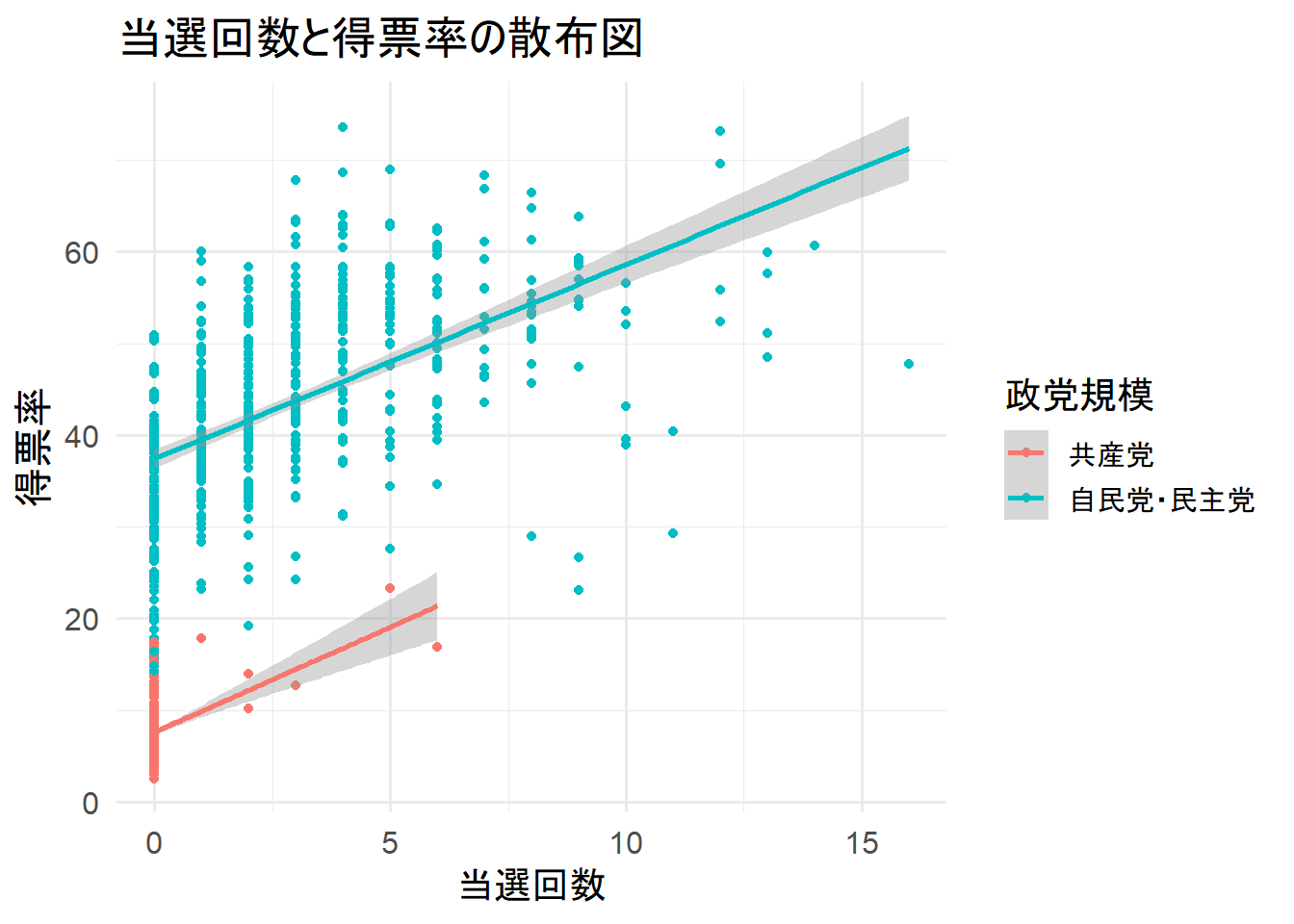
title = "当選回数と得票率の散布図")
正の相関が見られる。
回帰直線が外れ値に引っ張られている様子は見えない。
data %>%
ggplot(aes(x = nocand,
y = voteshare,
color = factor(party_size))) +
geom_point() +
geom_smooth(method = lm) +
scale_color_discrete(name = "政党規模",
breaks = c("0", "1"),
labels = c("共産党", "自民党・民主党")) +
labs(x = "候補者数",
y = "得票率",
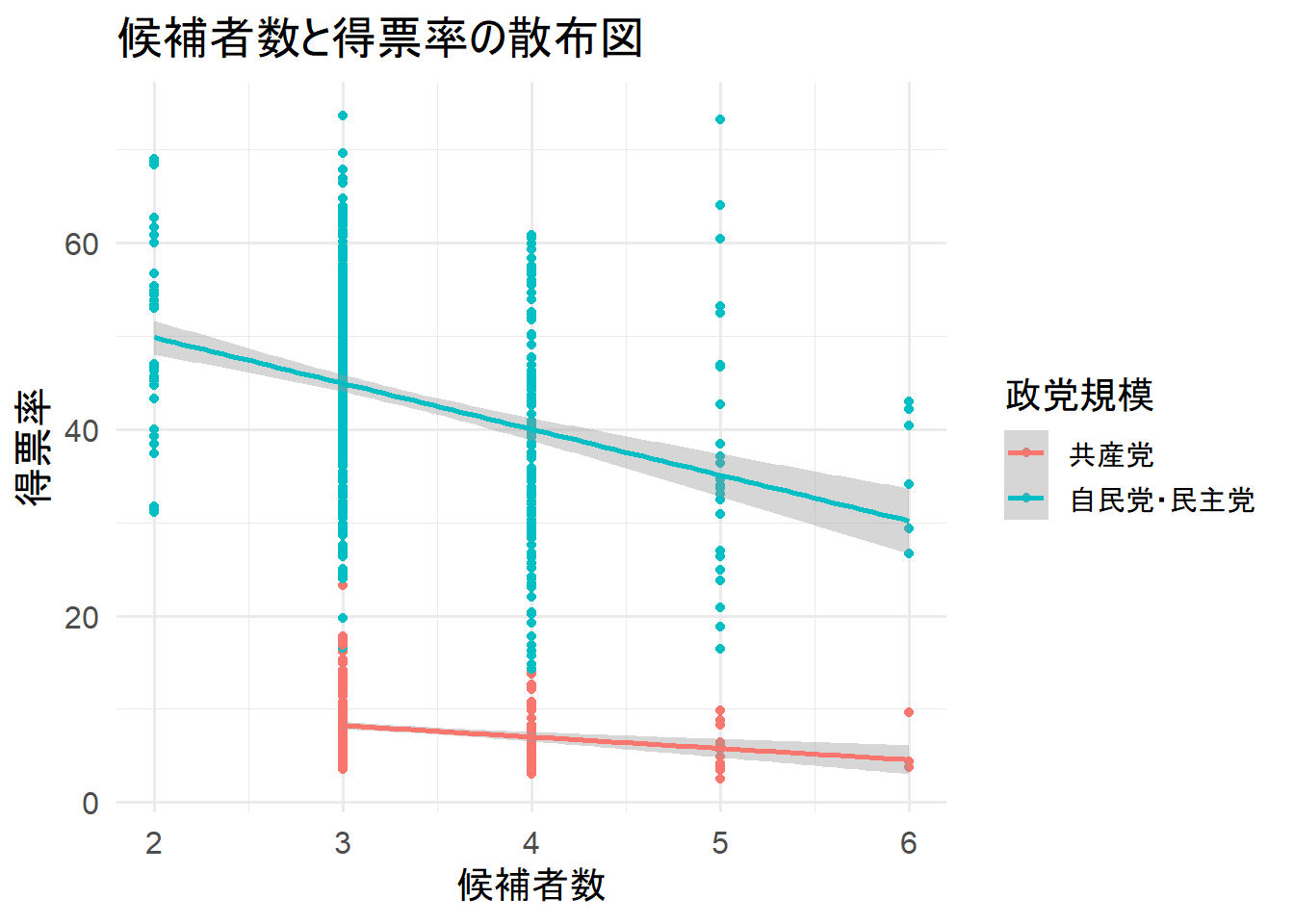
title = "候補者数と得票率の散布図")
負の相関が見られる。
回帰直線が外れ値に引っ張られている様子は見えない。
data %>%
ggplot(aes(x = party_size,
y = voteshare,
fill = factor(party_size))) +
geom_boxplot() +
scale_fill_discrete(name = "政党規模",
breaks = c("0", "1"),
labels = c("共産党", "自民党・民主党")) +
labs(x = "政党規模ダミー",
y = "得票率",
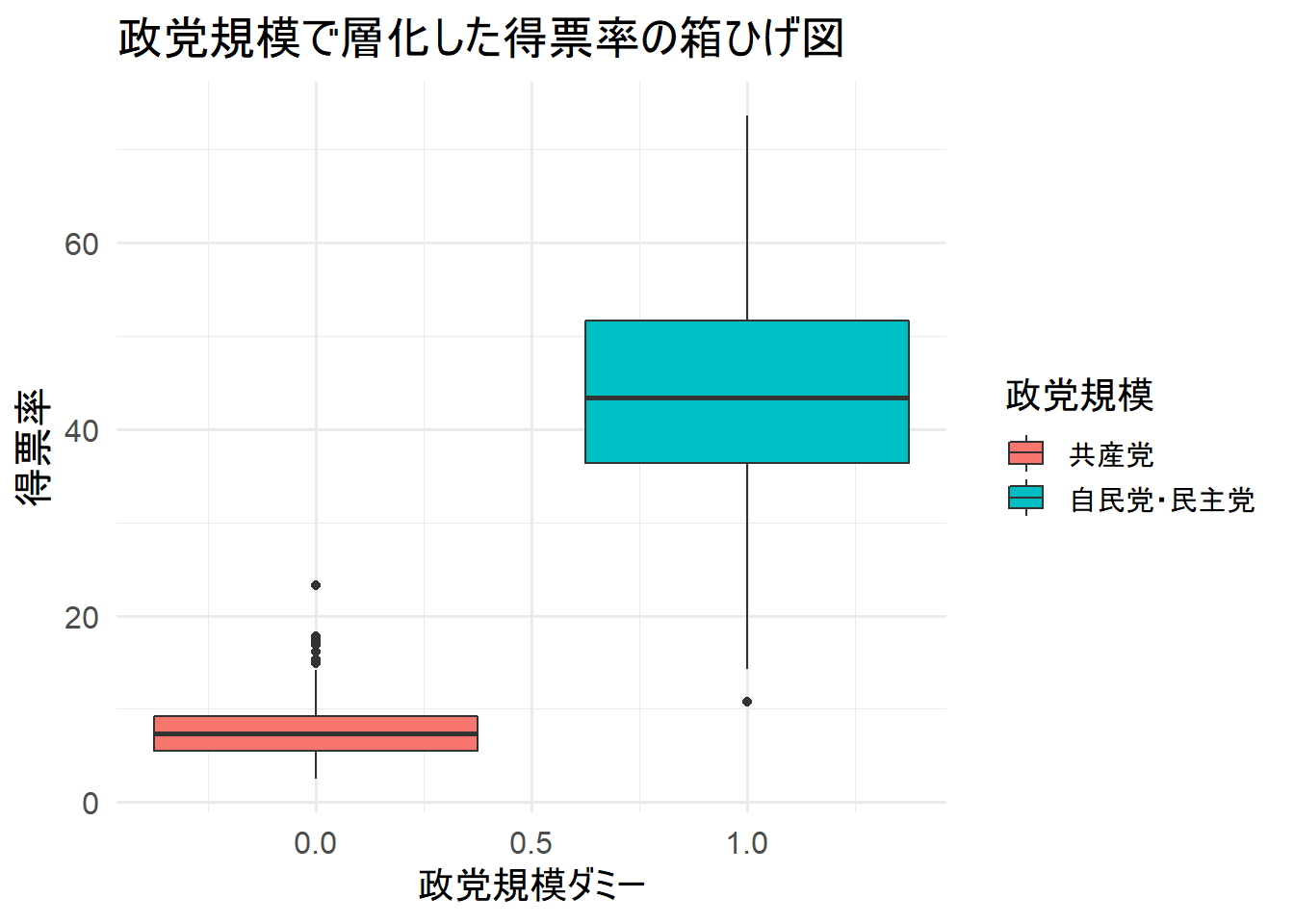
title = "政党規模で層化した得票率の箱ひげ図")
政党規模が大きいほうが、得票率が高いようだ。
そのため、政党規模のダミー変数を投入する必要性が確かにあるようだ。
5. 重回帰分析
5-1. 重回帰分析の実行
得票率 = 選挙費用 + 当選回数 + 候補者数 + 政党規模ダミー
これが重回帰式だ。Rで重回帰式を書くと、以下のようになる。
model <- lm(voteshare ~ exppv + previous + nocand + party_size, data = data)
また、独立変数の有意性をしっかり確認するために統制変数を1個づつ足していく。
そして、以下のように結果の表を記述する。
lm1 <- lm(voteshare ~ exppv, data = data)
lm2 <- lm(voteshare ~ exppv + previous, data = data)
lm3 <- lm(voteshare ~ exppv + previous + nocand, data = data)
# 要約統計量をHTMLで出力する。
# チャンクオプションにresults='asis'を忘れないように
stargazer(lm1, lm2, lm3, model,
type = "html",
style = "ajps",
digits = 2,
align = T, # 中央揃え
keep.stat = c("n", "adj.rsq", "f"), # 下の方で表示する統計量
dep.var.labels = "得票率",
covariate.labels = c("選挙費用", "当選回数",
"候補者数", "政党規模"))
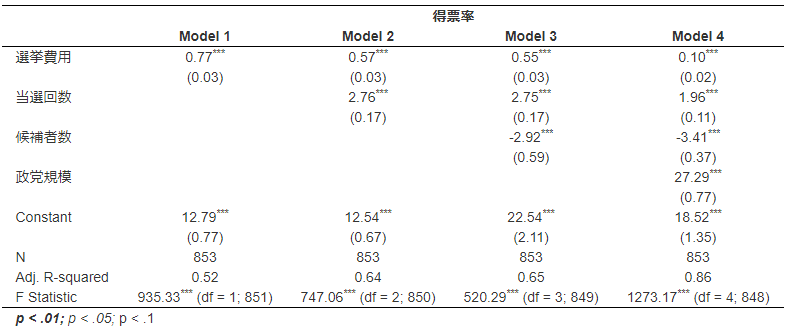
選挙費用が統計的に有意であることは確かだが、統制変数を投入したところ偏回帰係数が小さくなった。
そのため、有権者一人当たりの選挙費用を10円増やさなければ得票率が1%pt上昇しない。
また、政党規模が大きい場合(自民党。民主党所属の場合)、得票率が平均して27.29%ptも高いことが分かった。
Model4のAdj.R-squaredを見ると0.86とあり、従属変数である得票率の分散を86%をこのモデルで説明できたことを示す。
標準化偏回帰係数(beta値)
# beta値を計算する
lm.beta(model)
exppv previous nocand party_size
0.09226852 0.27613890 -0.11927921 0.67081178
また、標準化偏回帰係数を算出する。
独立変数や統制変数の値を1SD増やした時に、従属変数のSDがどれだけ変化するかを示す。
beta値を比較することで、複数の変数のうち、従属変数に1番影響を与えている変数は何かがわかる。
従属変数への影響力は、政党規模 > 当選回数 > 候補者数 > 選挙費用の順となっている。
つまり、選挙費用が従属変数に与える影響力は小さいということが分かる
5-2. モデルの診断
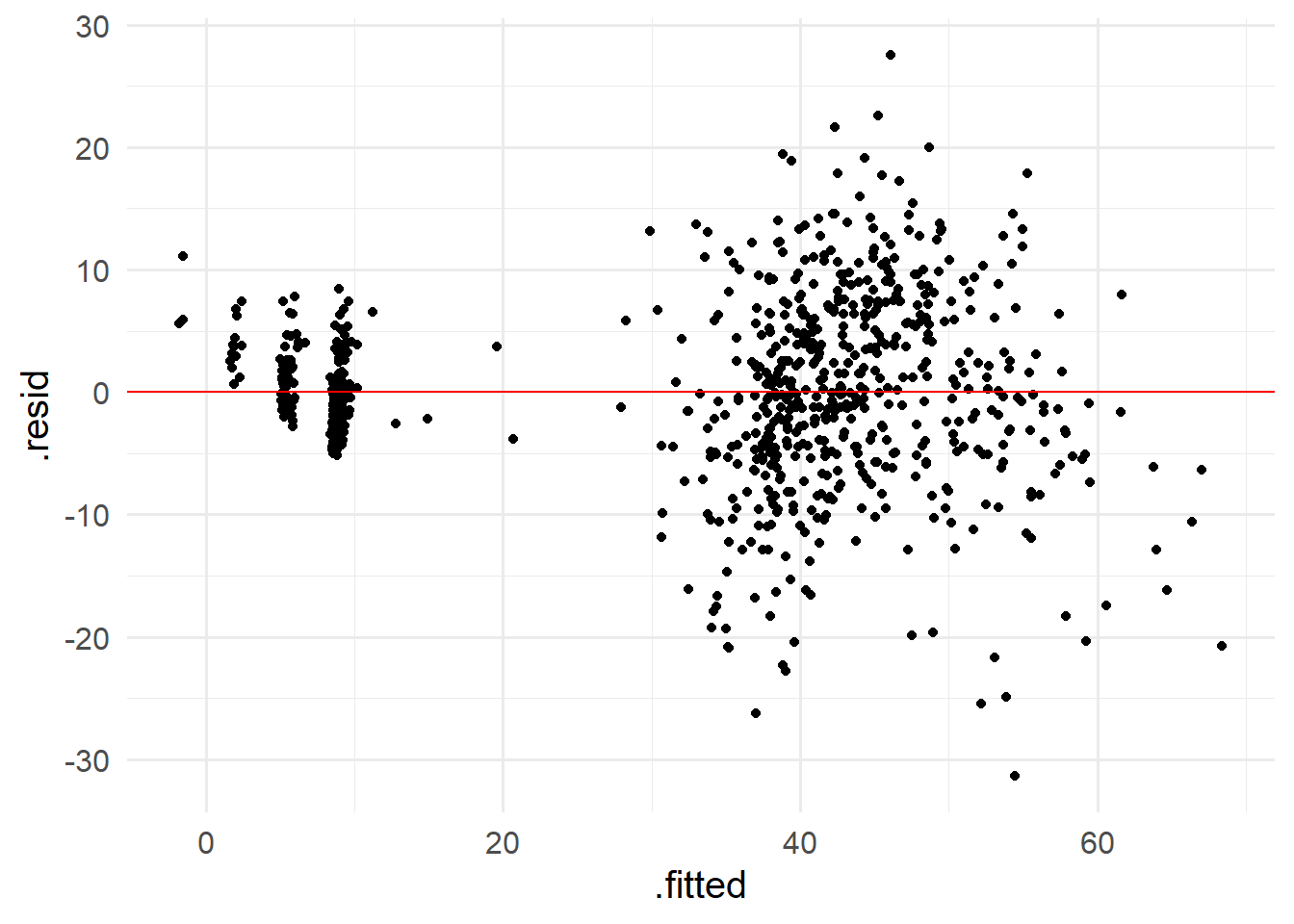
残差プロット
model %>%
augment() %>%
ggplot(aes(x = .fitted, y = .resid)) +
geom_point() +
geom_hline(yintercept = 0, color = "red")
残差にパターンはなさそうなので、残差が独立であるといえる。
しかし、残差の分散が均一ではないため、推定が効率的ではない。ただ、回帰直線自体が誤っているわけではないので、回帰分析をしてはいけないということではない。
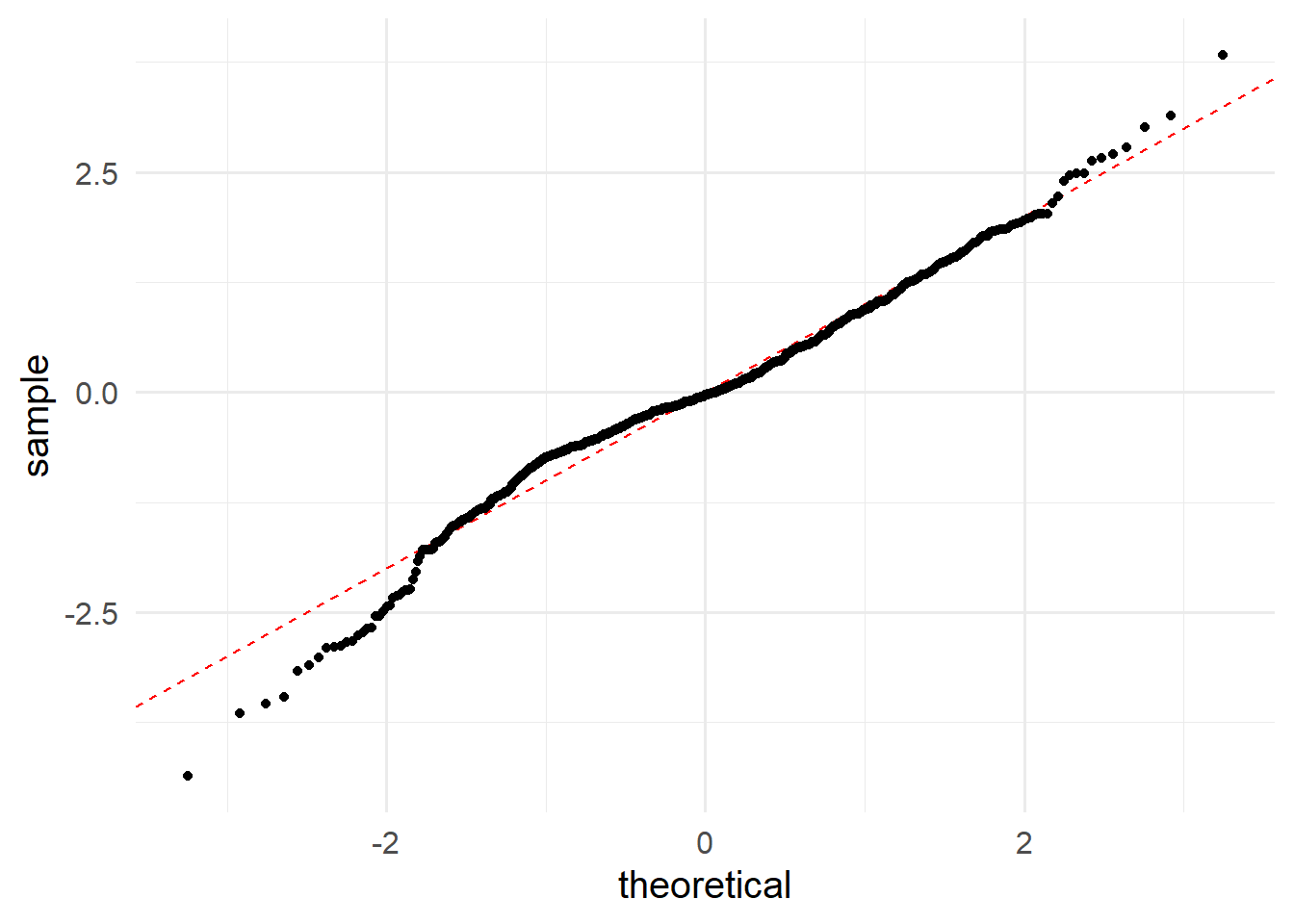
Q-Qプロット
model %>%
augment() %>%
mutate(z_res = (.resid - mean(.resid)) / sd(.resid)) %>%
ggplot(aes(sample = z_res)) +
geom_abline(a = 0, b = 1, linetype = 2, color = "red") +
geom_qq()
回帰分析の前提条件として、誤差分布の正規性がある。
Q-Qプロットの赤いラインに点が集まっていれば、誤差が正規分布しているということ。
多重共線性
# 多重共線性の確認
vif(model)
exppv previous nocand party_size
2.209048 1.390673 1.014492 2.147321
独立変数や統制変数の間で相関関係があることを多重共線性があるという。
分散拡大係数 (VIF: Variance Inflation Factor) による診断で多重共線性の有無を判断する。
VIFが10より大きければ、多重共線性ありと判断する。
多重共線性がある場合は、該当する説明変数をモデルから外して再度、回帰分析をする。
5-3. 点・区間推定の可視化
# 95%信頼区間の計算
CI <- model %>%
tidy() %>%
mutate(lower = estimate + qnorm(0.025) * std.error,
upper = estimate + qnorm(0.975) * std.error) %>%
filter(!term == "(Intercept)")
# キャタピラープロット
CI %>%
transform(term = factor(term, levels = c("previous", "party_size", "nocand", "exppv"))) %>% #変数の並び替え
ggplot() +
geom_line(aes(x = term,
y = estimate),
color = "blue",
size = 3) +
geom_pointrange(aes(x = term,
y = estimate,
ymin = lower,
ymax = upper),
color = "blue",
size = 1) +
geom_hline(yintercept = 0,
linetype = 2,
color = "red") +
geom_text(aes(x = term,
y = estimate,
label = round(estimate, 2)),
vjust = -1) +
scale_x_discrete(labels = c("exppv" = "選挙費用",
"nocand" = "候補者数",
"party_size" = "政党規模",
"previous" = "当選回数")) +
scale_y_continuous(breaks = seq(0, 30, length = 7)) +
labs(x = NULL,
y = "95%信頼区間") +
coord_flip()
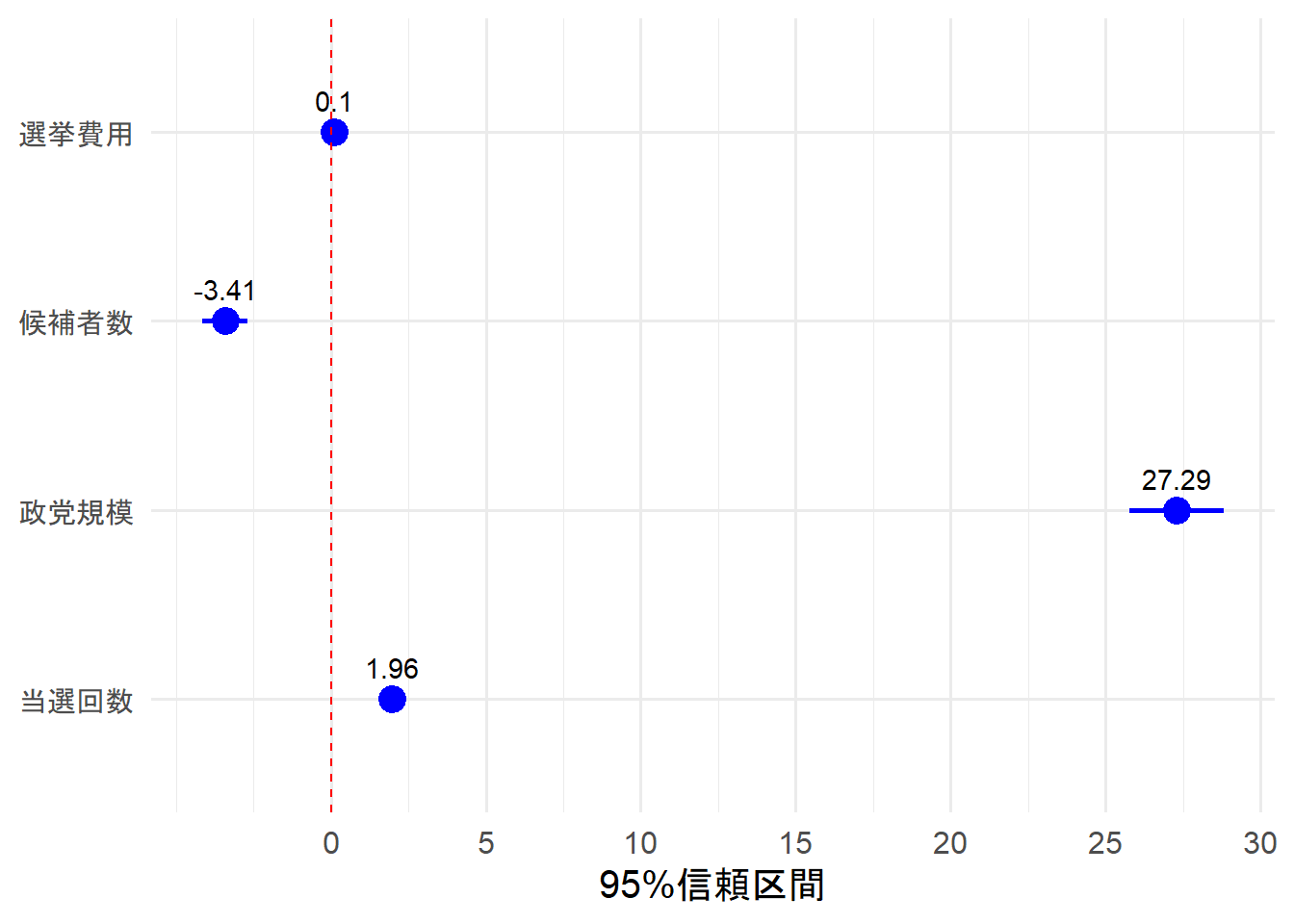
丸点が点推定、横棒が区間推定。つまり、区間推定が狭いと推定が正確であると言える。
区間推定を表す横棒が0のラインを触れると傾きが0のため、統計的有意性が無いとわかる。
点推定が0にほぼ触れているのに統計的に有意である場合は係数を確認し、十分小さい場合は実質的な有意性が無いと判断する。
選挙費用の実質的有意性は無いと判断しても良さそうだ。
5-4. 得票率の予測値
pred <- function(x){
model %>%
predict(newdata = data.frame(
exppv = min(data$exppv):max(data$exppv),
previous = mean(data$previous),
nocand = mean(data$nocand),
party_size = x),
se.fit = T,
formula = model) %>%
as.data.frame() %>%
mutate("upper" = fit + qnorm(0.975) * se.fit,
"lower" = fit + qnorm(0.025) * se.fit,
exppv = min(data$exppv):max(data$exppv),
party_size = x)
}
data_pred <- lapply(X = 0:1, FUN = pred) %>% bind_rows()
data_pred %>%
ggplot(aes(x = exppv,
y = fit,
group = party_size)) +
geom_line() +
geom_ribbon(aes(ymin = lower,
ymax = upper,
fill = factor(party_size)),
alpha = .5,
show.legend = F) +
labs(x = "選挙費用", y = "得票率の予測値")
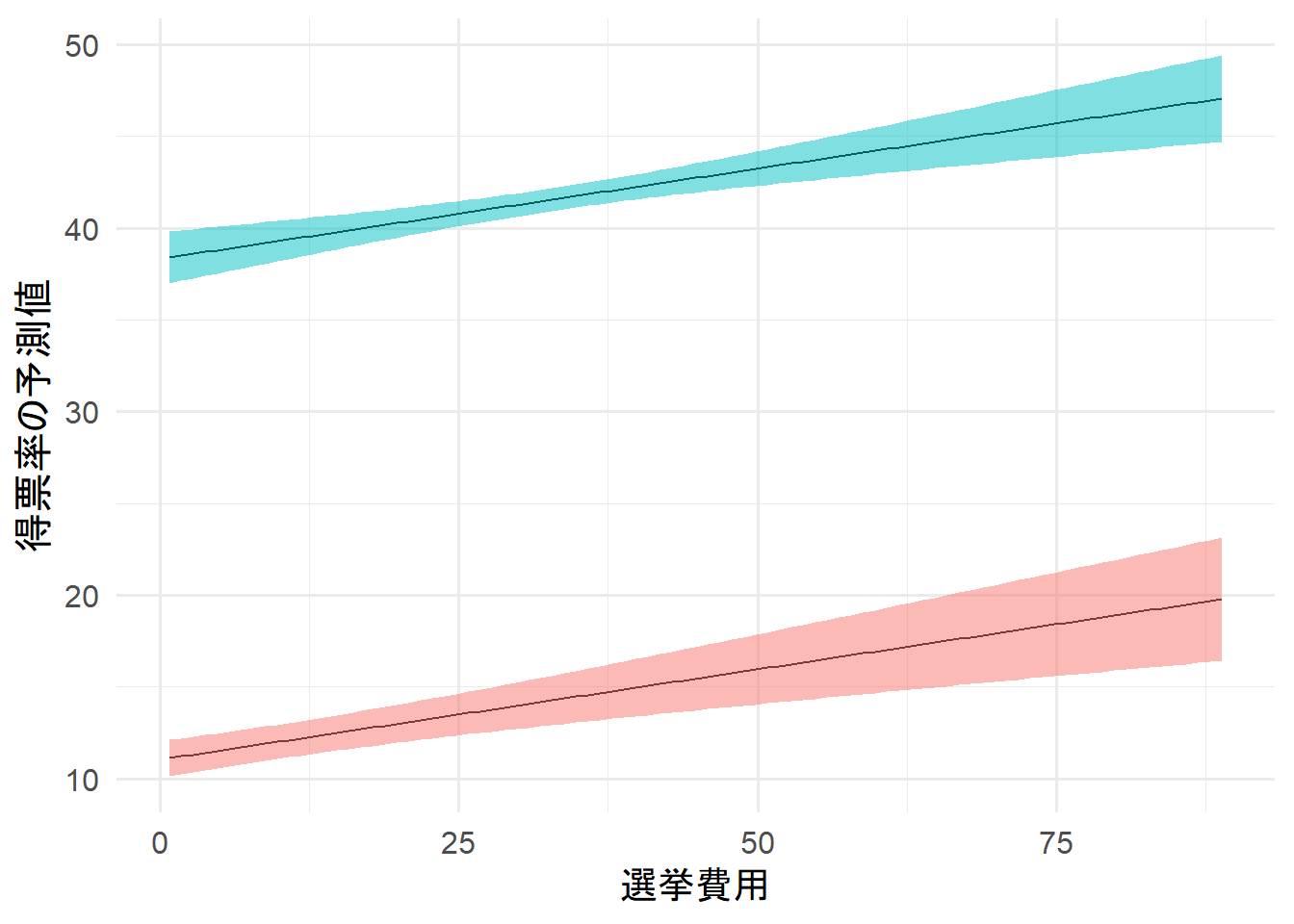
独立変数である選挙費用を最小値から最大値まで動かし、どのような得票率が得られるかを可視化した。
統制変数を平均値で固定している。
6. 分析結果の解釈
分析が終わったとしても、気を抜いてはいけない。
アカデミックな世界ならば論文に、ビジネスの世界なら報告書に、この分析結果をまとめ上げなくてはならない。
分析結果をまとめるには、重回帰分析の表だけではなく、キャタピラープロットやベータ値を出しておく必要がある。
今回の分析をまとめると、こうなる。
本分析は、「選挙費用を増やすことで票を得ることはできるのか」という問いに対し、重回帰分析を用いて解明を試みた。
その結果、有権者一人当たりの選挙費用が得票率と統計的に有意な関係にあるとわかった。しかし、統制変数よりもbeta値が小さく、影響は小さいと考えざるを得ない。
また、キャタピラープロットを図示した結果、区間推定は非常に短く、点推定は相当程度正確であると言えるが、推定値の0のラインに触れているように見え、有権者一人当たりの選挙費用を10円増やしても得票率が1%ptしか上昇しないことから、実質的な有意性は無いと判断しても良い。
ちなみに、有権者一人当たりの選挙費用を10円増やすというのは、有権者数*10円ということであり、有権者が10万人ならば選挙費用を100万円増やすごとに得票率が1%ptしか上昇しないということである。
ただ、、統制変数を平均値に固定し、選挙費用を観測値の最小値から最大値まで動かして得票率の予測値を可視化すると、
その結果、政党規模によって切片が異なり、所属する政党の規模によって選挙費用を高くする意味があるかないかが変化することがわかった。
政党規模が大きいと切片が高く、選挙費用を高くすることで当選が視野に入るぐらい得票率が高くなるようだ。
逆に、政党規模が小さいと切片が低く、選挙費用を高くしても当選が難しいとわかる。
そのため、より厳密にいえば、政党規模が大きいと選挙費用は実質的に有意であると言える。
以上のようになる。
論文であればもう少し論文の目的を振り返っても良いだろう。
enjoy !