GANを理解したかったのですが、数式の意味がわからなかったので調べました。5時間くらいかけて、なんとなくわかった気がしたので書いておきます。
概要
今回は、こちらのGAN論文の数式の意味を調べました。
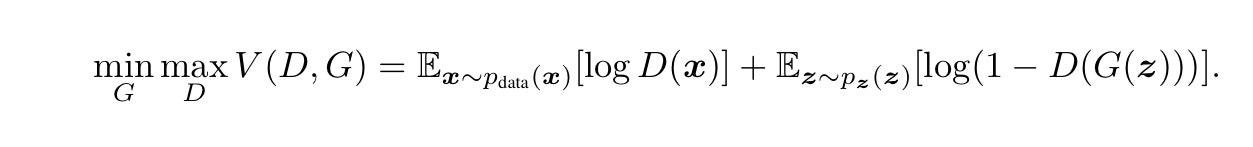
DはDiscriminator(識別器)、GはGenerator(生成器)を意味します。Dを騙すG, Gに騙されないDを目指して、DとGを学習させていくようです。
左辺
左辺は、Vを最大にするDと、Vを最小にするGを選択した際の、Vの値という意味でしょうか?
ミニマックス問題というものが関係しているようなので、wikipediaで調べてみると、
ミニマックス法(みにまっくすほう、英: minimax)またはミニマックス探索とは、想定される最大の損害が最小になるように決断を行う戦略のこと
なので、この数式をミニマックス問題として理解すると、DがVを最大化する場合に「Vを最小にするG」を選ぶ問題、となるようです。
Gの学習がミニマックス問題に当たる気がします。
右辺
Dは0~1の値を返すモデルだと理解しました。
正解ラベルは、オリジナルのデータには1、Gが生成したデータには0が振られている、という認識です。
log(0)とlog(1)の計算結果
log(D)がどんな特徴を持つのか、調べました。Dは0~1の値を返すので、D=1とD=0の場合の結果を確認してみます。
log(1) = 0
log(0) = -∞
つまり、1に近いほど値が大きくなり(0に近づき)、0に近いほど値が小さくなる(-∞に近づく)という特徴があるようです。
右辺第一項
xは教師データなので、1に近い値を返せるほど正しいモデルとなります。
logD(x)は、D(x)が1に近いほど値が0に近づき、0に近いほど小さい値(-∞に近い値)になります。
右辺第二項
Gが生成したデータなので、Dは0に近い値を返せるほど、正しいモデルとなります。
log(1-D(G(z))は、D(G(z))が1に近いほど小さい値になり、0に近いほど大きな値(0)に近づきます。
学習方法
冒頭のGANの論文の説明を読むと、DとGの学習を交互に進めるようです。

Dの学習
Gを固定して、Vが最大化するように学習します。右辺全体を最大化します。
Gの学習
Dを固定してVが最小化するように学習します。右辺の第二項だけを最小化するようです。
終わりに
雰囲気はわかった気がするので、コードとして実装してみたいと思います。