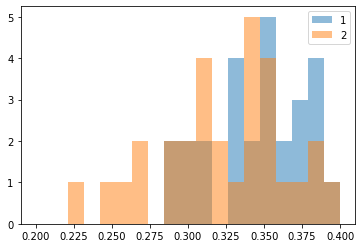仮説検定とは
観測されたデータをもとに母集団に関する仮説の是非を判定する。
問題設定
カントー地方では各地でコラッタが出現する。
出現する場所は「1番道路、2番道路」で出現することがわかっている。
これらの場所でコラッタを捕獲し、体長を観測し、生息場所が観測量に与える影響を調べる。
母集団の設定
各地のコラッタの母集団の統計量を乱数により設定した。
(現実世界でコラッタはいないので母集団を適当に設定してそこからコラッタをサンプリングします。)
コラッタの体長xは平均μ標準偏差σの正規分布に従う
x ~ N(μ, σ^2)
以下のコードで各道路に出現するコラッタの体長の母平均・母分散を設定した。
places = ['1番道路', '2番道路']
populations = {}
for place in places:
mu = random.uniform(0.30, 0.35) # 体長の母集団平均0.30~0.35の一様乱数
sigma = random.uniform(0.04, 0.042) # 体長の母集団分散0.04~0.042の一様乱数
populations[place] = {'mu': mu, 'sigma': sigma}
検定を行なった経緯
ポケモン研究の権威である大木戸博士はある研究のために各地から収集されたコラッタを観察している時、地域によってコラッタの体長が違うことに気がついた。各地から30匹ずつ集められたコラッタの体長のヒストグラムは次のとおりであった。
どうやら一番道路に出現するコラッタは二番道路に出現するコラッタより大きい傾向がありそうだと言える。
大木戸博士はこの説を論文として発表するため仮説検定を実施することにした。
サンプリングとヒストグラム描画に使用したコードは以下の通り。
# 母集団からサンプリングする
def sample_rattata(size, place, populations):
population = populations[place]
mu, sigma = population['mu'], population['sigma']
heights = np.random.normal(mu, sigma, size)
return heights
sample_size = 30
samples = {}
for place in places:
sample = sample_rattata(sample_size, place, populations)
samples[place] = sample
print(samples)
出力
{'1番道路': array([0.41545733, 0.35883398, 0.38285429, 0.43525381, 0.41975446,
0.30164851, 0.38166488, 0.33593736, 0.33793587, 0.35926746,
0.34820119, 0.40259658, 0.37381627, 0.34727254, 0.36064848,
0.35607389, 0.40424914, 0.33370376, 0.35521838, 0.30676253,
0.2362314 , 0.36935666, 0.37810895, 0.31140944, 0.43645202,
0.28184178, 0.3441208 , 0.33444998, 0.40585581, 0.40322286]),
'2番道路': array([0.32730671, 0.33635091, 0.28505742, 0.240771 , 0.30693193,
0.3273635 , 0.37087729, 0.36974641, 0.30533494, 0.30877993,
0.27854348, 0.26349253, 0.25189421, 0.40006977, 0.30037858,
0.30327876, 0.27026803, 0.3525308 , 0.25563693, 0.3124088 ,
0.28474621, 0.33670503, 0.30033186, 0.27319192, 0.3198867 ,
0.33838366, 0.32372371, 0.33328409, 0.29532722, 0.30633109])}
ヒストグラムを描画
fig, ax = plt.subplots()
for place in places:
sample = samples[place]
plt.hist(sample, alpha=0.5, label=place[0])
ax.legend()
plt.show()
(上に掲載したヒストグラムを出力)
検定の設計
今回注目しているのはコラッタの体長の大小、すなわち母集団の平均の差$\delta_0=\mu_A - \mu_B$である。対立仮説、帰無仮説は以下の通り。
対立仮説
一番道路のコラッタの体長の母集団平均は二番道路のそれよりも大きい
\delta_0 > 0
帰無仮説
一番道路のコラッタと二番道路のコラッタの体長の母集団平均に差はない
\delta_0 = 0
確率分布に関する仮定
母集団の分布を仮定する場合と仮定しない場合で検定の手続きが異なり、分布を仮定する場合はパラメトリック法、仮定しない場合はノンパラメトリック法となる。
今回は、
- コラッタの体長は正規分布に従うと仮定する。(パラメトリック。実際母集団は正規分布としたが、標本の観測者からは自明でない。)
- 各生息地で体長について共通の母分散を仮定する。(実際母分散は共通ではないが、これも観測者からはわからない。ひとまず大きな乖離がないと仮定。)
以上の仮定のもとで2標本の平均の検定を行う。
また、有意水準$\alpha=0.05$の片側検定とする。
今回の検定は正規分布の2標本問題のうち、分散が未知(2標本間で等しい)のものとして考えられ、このような場合、t検定が用いられる。
検定統計量
一番道路の標本:A
二番道路の標本:B
として各群の標本分散は、
s_A^2=\frac{1}{n_A-1}\Sigma_{i=1}^{n_A}(X_{A_i}-\bar{X_A}) \\
s_B^2=\frac{1}{n_B-1}\Sigma_{i=1}^{n_B}(X_{B_i}-\bar{X_B})
共通の母分散$\sigma^2$の不偏推定量は、
s^2=\frac{(n_A-1)s_A^2 + (n_B-1)s_B^2}{n_A + n_B - 2}
検定統計量は、
T=\frac{\bar{X_A} - \bar{X_B} - \delta_0}{s \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}}
これは自由度$n_A+n_B-2$のt分布に従う。
サンプルサイズの決定
まず、効果量を決めてサンプルサイズを計算する。
2群の平均値の差の大きさを示す効果量としてよく知られているCohenのdを使う。
d = \frac{|\bar{X_A}-\bar{X_B}|}{s}\\
s = \sqrt{\frac{n_As_A^2+n_Bs_B^2}{n_A+n_B}}
サンプルサイズを求めるための等式は次の通り。
t_{\alpha/2} + t_{\beta} = \frac{|\bar{X_A}-\bar{X_B}|}{s \sqrt{\frac{1}{n_A} + \frac{1}{n_B}}} = \frac{d}{\sqrt{\frac{1}{n_A} + \frac{1}{n_B}}}
効果量$d=0.5$、有意水準$\alpha=0.05$、検出力$\beta=0.8$、$n_A=n_B$としてこれを解いてサンプル数が得られる。
しかし、t分布はサンプル数によって変化するため解くのは容易ではない。
そこで今回は下記のサイトを利用してサンプル数を得た。
https://keisan.casio.jp/exec/user/1491310412
有意水準$\alpha$、効果量$d$を固定して、サンプル数$n=n_A=n_B$を変化させて必要な検出力になるサンプル数を調べている。
求められたサンプル数は$n=n_A=n_B=51$であった。
※効果量ってなんなん?
効果量は検定する要因が与える効果の大小を表す。
大きい小さいは標本分散と比べて判断されている(正規化されている)。
仮説検定では差異の有無を判定するが、差異の大きさはこの効果量から判断する。
効果量は仮説検定に用いる標本のサイズを決定するために必要になる。
見たい差が小さい場合サンプルサイズが大きくないと微妙な差を判断できない。
極端な話、コラッタの体長の母集団の平均の差が$0.000000000000001$[cm]でもサンプルサイズが無限なら差があることがわかる。
(標本平均が母集団平均に収束するので直接比べたらいい)
実際には有限個なので仮説検定で判断する。
逆にサンプルサイズが大きすぎると実質的に差がないといえるほどの小さな差を検出してしまう。
例えば、無作為にコラッタを分けても有限個の集団であれば2群の間に0以上の体長の差は生じる。
このようなものを差があると判断してしまうとまずい(偶然の差と判断してほしい)のでサンプルサイズは大きいほど良いというものでもない。
そこでちょうどいいサンプルサイズを決めるためにあらかじめどれくらいの差を差と見做すのかを効果量として設定しておく。
検定の実施
標本A, Bを新たに集められた一番道路、二番道路から51匹ずつのコラッタとして検定統計量を計算する。
# サンプリング
sample_size = 51
samples = {}
for place in places:
sample = sample_rattata(sample_size, place, populations)
samples[place] = sample
# 検定統計量の計算
X_A_bar = samples['1番道路'].mean()
X_B_bar = samples['2番道路'].mean()
s_A = samples['1番道路'].std()
s_B = samples['2番道路'].std()
s2 = ((sample_size-1)*s_A**2 + (sample_size-1)*s_B**2) / (2*sample_size - 2)
s = np.sqrt(s2)
T = (X_A_bar - X_B_bar) / (s * np.sqrt(2/sample_size))
print(T)
出力
2.585773686831046
棄却限界値は自由度が$2n-2$のt分布の上側2.5%点である。自由度が100と大きいので正規分布とみなして棄却限界値を求めると、
t_{0.025}(100)\simeq z_{0.025}=1.96
であり、帰無仮説は棄却される。
シード値
以下のシード値を最初に設定してコードを実行すると同じ乱数が生成されて本記事の検定を再現できます。
random.seed(0)
np.random.seed(0)
終わりに
実際に具体的な問題設定をして検定してみて理解が深まった。
最後まで読んでくれた方ありがとうございます。
ご意見ご感想いただけると嬉しいです。