こんにちはFooQooです.
今回は,ポアソン分布に従う時系列データから3$\sigma$法を用いて異常検知することについてまとめます.
ポアソン分布
はじめに,ポアソン分布についてwikipediaで定義を確認しましょう.
所与の時間間隔で発生する離散的な事象を数える特定の確率変数Xを持つ離散確率分布
確率質量関数は次の式です.
P(k | \lambda) = e^{-\lambda} \frac{\lambda^k}{k!}
よくある例えで,1年間に交通事故がk回発生する確率がポアソン分布に従っていると言われています.
1日における交通事故の発生確率がpとすると,それがk回発生する確率は,
P(k) = {}_n C_k p^{k} (1-p)^{n-k}
で求まります.ポアソン分布は以上の式の$n \rightarrow \infty$を考えます.
導出
先ほどの問題から,ポアソン分布の確率質量関数を導出します.
まずは前提について,
- 成功確率が$\frac{\lambda}{n}$となる独立な試行を$n$回行います.
- $n$回の試行のうち$k$回成功する確率は,${}_n C_k {(\frac{\lambda}{n})}^k (1-\frac{\lambda}{n})^{n-k}$
これの$n \rightarrow \infty$を計算します.
\begin{align}
P(k) &= \lim_{n \to \infty} {}_n C_k {(\frac{\lambda}{n})}^k (1-\frac{\lambda}{n})^{n-k} \\
&= \lim_{n \to \infty} \frac{n!}{k!(n-k)!} {(\frac{\lambda}{n})}^k (1-\frac{\lambda}{n})^{n-k} \\
&= \lim_{n \to \infty} \frac{n!}{k!(n-k)!} {(\frac{\lambda}{n})}^k (1-\frac{\lambda}{n})^{n} (1-\frac{\lambda}{n})^{-k} \\
&= \lim_{n \to \infty} \frac{n!}{n^k(n-k)!} {\frac{\lambda^k}{k!}} (1-\frac{\lambda}{n})^{n} (1-\frac{\lambda}{n})^{-k}
\end{align}
ここで整理できる極限をまとめます.
$
\begin{eqnarray*}
\lim_{n \to \infty} \frac{n!}{n^k(n-k)!}
&=& \lim_{n \to \infty} \frac{n(n-1)\cdots(2)(1)}{(n-k)(n-k-1)\cdots(2)(1)} \frac{1}{n^k} \
&=& \lim_{n \to \infty} \frac{n(n-1)\cdots(n-k+1)}{n^k} \
&=& \lim_{n \to \infty} 1(1-\frac{1}{n})\cdots(1-\frac{k-1}{n}) \
&=& \prod_{k} 1 = 1
\end{eqnarray*}
$
ネイピア数の定義 $e=\lim_{n \to \infty}(1+\frac{1}{n})^n$より,
$
\begin{eqnarray*}
\lim_{n \to \infty} (1-\frac{\lambda}{n})^{n}
= (\lim_{n \to \infty} (1+\frac{1}{\frac{n}{-\lambda}})^{\frac{n}{-\lambda}})^{-\lambda}
= e^{-\lambda}
\end{eqnarray*}
$
次は簡単な極限の計算です.
$
\begin{eqnarray*}
\lim_{n \to \infty} (1-\frac{\lambda}{n})^{-k}
= 1^{-k} = 1
\end{eqnarray*}
$
以上の極限を確率の式に代入すると,
$
\begin{eqnarray*}
P(k)
&=& \lim_{n \to \infty} \frac{n!}{n^k(n-k)!} {\frac{\lambda^k}{k!}} (1-\frac{\lambda}{n})^{n} (1-\frac{\lambda}{n})^{-k} \
&=& 1 \cdot {\frac{\lambda^k}{k!}} \cdot e^{-\lambda} \cdot 1 \
&=& e^{-\lambda} \frac{\lambda^k}{k!}
\end{eqnarray*}
$
となり無事導出できました!!
3σ法
3$\sigma$法は,あるデータ$X$の中の値$X_t$が,以下の条件を満たす時,$X_t$を外れ値とする手法です.
$
\begin{eqnarray*}
X_t > \mu + 3\sigma
\end{eqnarray*}
$
$\mu$は$X$の平均値,$\sigma$は$X$の標準偏差です.
主に,工場の品質管理で用いられており,データが正規分布の場合は,3$\sigma$法に引っかからない値の範囲は全体の99.7%になります.
水沼の修士論文ではツイートのバースト検出でも用いられました.
ポアソン分布を持つデータへの適用
ここで気になったのが,ポアソン分布に従うデータに対して,$3\sigma$法を適用した時に外れ値以外は全体の何%になるかということです.
実際に計算してみましょう.
まずポアソン分布における平均と標準偏差から3$\sigma$の値は,
$
\begin{eqnarray*}
x = \lambda + 3\sqrt{\lambda}
\end{eqnarray*}
$
となります.
この値を用いて$P(X \leq x)$を計算します.ポアソン分布の累積確率関数は次の式となります.
$
\begin{eqnarray*}
P(X \leq x) = F(x) = e^{-\lambda} \sum_{i=0}^{floor(x)}\frac{\lambda^i}{i!}
\end{eqnarray*}
$
試しに$\lambda=10,100,1000$の時の値を計算しました.
計算に使用したソースコード及び結果を示します.
from scipy.stats import poisson
from math import sqrt
from math import floor
lams = [10,100,1000]
for lam in lams:
th = floor(lam + 3*sqrt(lam))
cdf = poisson.cdf(th,lam)
print('閾値:{} 確率:{}'.format(th,round(cdf,3)))
表1 : 各パラメータの際の閾値と累積確率
| $\lambda$ | 10 | 100 | 1000 |
|---|---|---|---|
| threshold | 19 | 130 | 1094 |
| probability | 0.997 | 0.998 | 0.998 |
正規分布の際と似たような結果になっています.使えそうですね.
時系列データの考慮
ここで我々が適用させたいデータが時系列データであることを考えます.
新しく流入したデータが,これまでのデータの平均と標準偏差を用いた$3\sigma$法による閾値で判断する必要があるため,平均と標準偏差を求めるサンプルは新規流入データ以前のデータを用います.
ここからはお好みで,過去全てのデータを用いるのか,あるいはウィンドウ幅を決めてスライディングウィンドウでサンプルを取ればよいでしょう.
出現が稀な時系列データに対して
また通常状態において,ほとんど出現しない頻度データに対しては,数件程度が値が増えただけで異常検知されてしまうので,あらかじめ別に下限となる値を設ける必要があります.
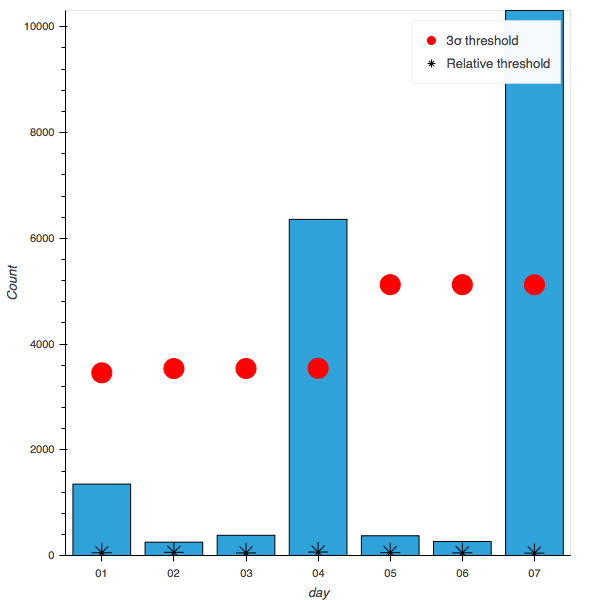
下の図は,Twitterにおける特定のキーワードのバースト検出を仮定した例です.
この例では,全体のキーワードを頻度が高い順にソーティングし,逐次累積確率を求めて,その値が0.8を超えた時の頻度の値を下限としています.
もちろん経験則に従って,決めうちで値を設けてもよいでしょう.
おわりに
今回のエントリでは,ポアソン分布に従う時系列データから$3\sigma$法を用いて異常検知する方法についてまとめました.
時系列データからの異常検知方法は他にもたくさんあるので,時間があればまとめてみます.
この手法を利用するとTwitterにおける単語のバースト検出やログの解析ができると思うので興味があれば試して見てください!
ソーシャルメディア解析の視点で見るとKleinbergのバースト解析が有名ですが,この手法は実装が簡単なんで,個人的にオススメです.