はじめに
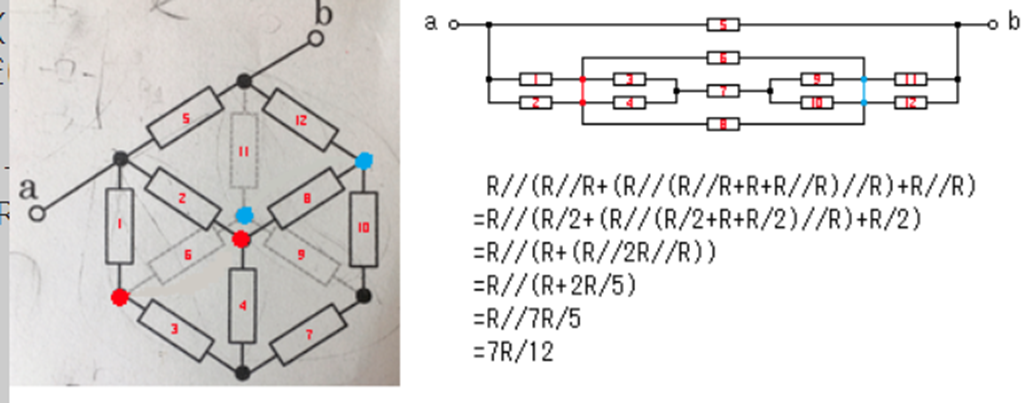
電験試験では、下図のような直並列に抵抗がつながった経路の合成インピーダンスを示す問題が出題される。
これらの問題は一般的に抵抗値は等しくRとし、その幾何学的対称性を通じて解を求める。
ただ、これらの問題が一般化された場合（R1≠R2・・・≠R12)の解法も必要と考え、その解をMatlabで求めた考え方と結果を記載する。
図は上記URLより引用
本文章の指針
同様の試みは先行文献で言及されている。主にキルヒホッフの第2法則にしたがい、下式を求めることで合成インピーダンスを計算している。
$\Sigma_{v \in G_u} \frac{V_u - V_v }{R} $
先行文献では、Rが固定値ではなく可変でも対応できるプログラムに言及されているが、具体的な計算手法については言及していない。そこで本文では、Rが可変になった際の計算手法を提示する。またその妥当性を検証する。
計算手順
先行文献より、接点ごとの電流の総和を行列式で表し、そのrrefをとることで解が求まる（らしい）。
ステップを以下に示す。
-
回路図を接点ごとに展開する。
ここで青四角の番号は抵抗のNo、◯字はノード点の数を表す。 -
あるノードnに流れ込む電流の総和を計算する。ここでRは可変のため、
抵抗値毎に計算し、その総和をとることで式を修正する。
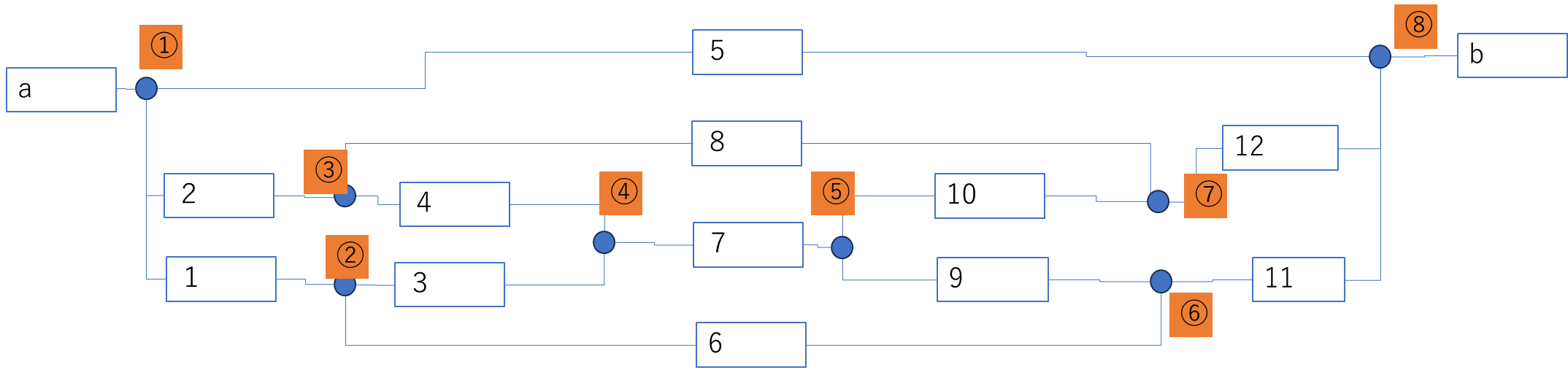
ex. n=①のノードに対しては、2の抵抗と1の抵抗、5の抵抗、および入口a から Iの電流が流れ込むため、下式の形で計算する。
$(V_1-V_3)/R_2 + (V_1-V_2)/R_1 + (V_8-V_2)/R_5 = I$ -
2を繰り返して、ノード点数×ノード点数の行列を作る。
-
上記と$I =[I,0, \dots ,-I]^T$を結合し、rref関数に入れることで、合成インピーダンスが計算できる。
実行コード
%% 変数定義
R1 = 1;
R2 = 1;
R3 = 1;
R4 = 1;
R5 = 1;
R6 = 1;
R7 = 1;
R8 = 1;
R9 = 1;
R10 = 1;
R11 = 1;
R12 = 1;
%% 行列定義
Matrix = [ 1/R1+1/R2+1/R5, -1/R1, -1/R2, 0, 0, 0, 0, -1/R5; ...
-1/R1, 1/R1+1/R3+1/R6, 0, -1/R3, 0, -1/R6, 0, 0; ... %miss1
-1/R2, 0, 1/R2+1/R4+1/R8, -1/R4, 0, 0, -1/R8, 0; ...
0, -1/R3, -1/R4, 1/R4+1/R3+1/R7, -1/R7, 0, 0, 0; ...
0, 0, 0, -1/R7, 1/R7+1/R10+1/R9, -1/R9, -1/R10, 0; ...
0, -1/R6, 0, 0, -1/R9, 1/R6+1/R9+1/R11, 0, -1/R11; ...
0, 0, -1/R8, 0, -1/R10, 0, 1/R8+1/R10+1/R12, -1/R12; ...
-1/R5, 0, 0, 0, 0, -1/R11,-1/R12,1/R5+1/R12+1/R11 ];
Iref = [1,0,0,0,0,0,0,-1]';
refMatrix = [Matrix Iref];
%rref化
[R,p] = rref(refMatrix);
disp(R)
%理論値
disp(7/12)
実行結果
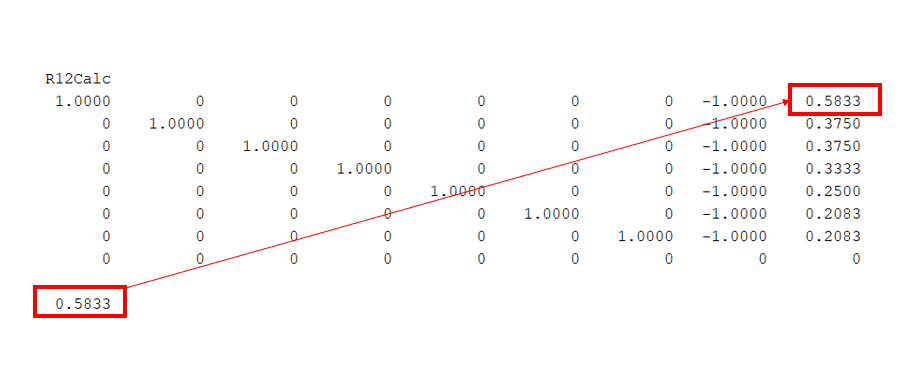
計算すると 下記のような行列が得られる。この右上が求めるa→bのインピーダンスになる。
今回はすべてR＝１と置いたので、正解が(7/12) =0.5833Ωとなるが、見事に一致している。
以上から、作成した式の妥当性が確認できた。
おわりに
本来ならR値をランダムに振って、式の妥当性を検証したかったかったが、その余力がなかった。
また次回以降に追記する予定である。