任意の点から円錐面までの最短距離を求める方法

はじめに

「ある点から円錐面までの最短距離を求める方法」を検索しても特にまとめられていないようなので，解法をまとめました．
ひとまず，数学的な解法だけ載せますが，せっかくQiitaにあげるので後日PythonもしくはC++でのプログラム例も書こうと思っています．

問題

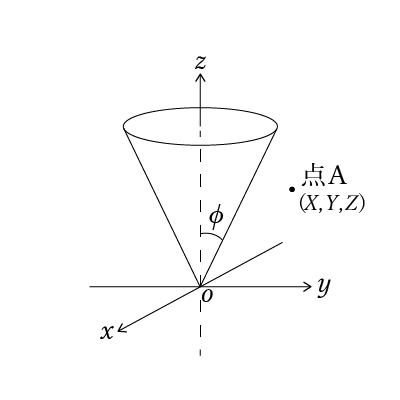
以下の円錐を使って考えます．
任意点A(X,Y,Z)から円錐表面までの最短距離を求めていきます．
円錐の中心軸と母線のなす角度はφです．

Step 1

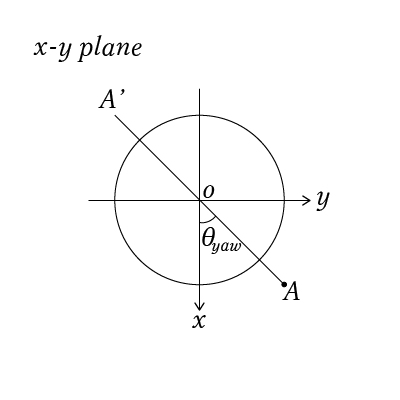
まず，点Aと円錐の中心Oを通る平面で，円錐を切ります．この平面をA-A'とします．
x軸と平面A-A'のなす角度をθ_yawとおきます．
これをxy平面に対して垂直方向から見ると，以下の図のようになります．

θ_yawは以下の式で表すことができます．
$$\theta_{yaw} = tan\frac{Y}{X} $$

Step 2

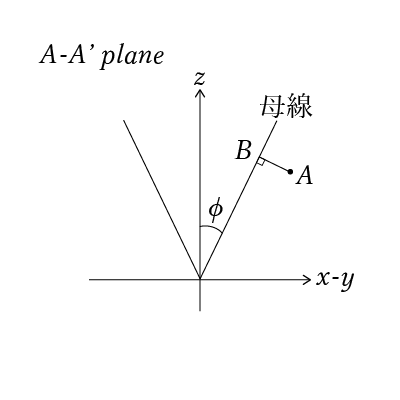
A-A'平面で切った断面図は下図になります．
ここで，点Aから母線まで垂線を引き，その線と母線との交点を点Bとします．

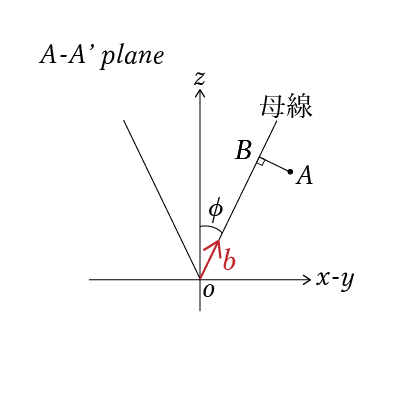
OBの単位ベクトル$\frac{\vec{OB}}{|\vec{OB}|}$を${\bf b}$とします．

${\bf b}$は以下の式で表せます．

{\bf b} =
\left( 
\begin{matrix}
sin\phi cos\theta_{yaw} \\
sin\phi sin\theta_{yaw} \\
cos\phi
\end{matrix}
\right)

図からわかるように，点Aと円錐の最短距離問題は，点Aと母線の最短距離問題に置き換えることができます．

Step 3

最後はベクトルを使って解いていきます．
$\vec{OB}┻\vec{BA}$なので，
$${\bf b} \cdot \vec{BA} = 0 $$
ここで，

\begin{eqnarray}
\vec{BA} &=& \vec{OA} - \vec{OB} \\
&=& \vec{OA} - t{\bf b} \ (tは媒介変数)
\end{eqnarray}

と表せます．
したがって，

\begin{eqnarray}
{\bf b}\cdot \vec{BA} &=& {\bf b}\cdot (\vec{OA}-t{\bf b}) \\
&=& {\bf b}\cdot \vec{OA}-t = 0
\end{eqnarray}

となります．
$$\therefore t = {\bf b} \cdot \vec{OA}$$
よって，$\vec{BA}$は，$\vec{BA}=\vec{OA}-t{\bf b}$となり，その大きさが求める距離となります．