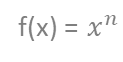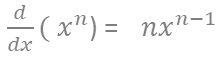文系卒エンジニアが機械学習を学ぶために数学を勉強してみた

Ⅰ．はじめに

１．まだ勉強中です。未完成の部分もありますが、今後完成させていこうと思います。長い目でみてやってください。
２．独学したものをまとめているので、厳密にいうと違っている部分があるかもしれないです。そこはぜひコメント欄でIssueつけてくれると助かります。
３．この記事は私個人というより数学を学びなおしたいエンジニアすべてに向けて書きたいと思っています。なので、わかりづらいところがあれば適宜わかりやすくしていきたいと思います。皆でいい記事にしていきたいです！
４．もともとパワポの資料に貼ってあったものを貼り付けているので、ちょっと時間がかかります＆綺麗ではないです。。。これからきれいにしていけるようにします！

Ⅱ．筆者について

ⅰ．文系私大卒。受験科目は国語英語日本史と、数学はⅠ・Aのみ。
ⅱ．通信事業者で基幹システム開発の上流工程を担当
ⅲ．もともと他社でSpringやDjangoを使ったWeb開発をしていた。
ⅳ．機械学習については、今年春から勉強開始

Ⅲ．この記事の目的と対象者

ⅰ．目的

　・機械学習、ディープラーニングを理論から理解するために数学を半年ちょっと勉強してきたので、その内容を少しずつ整理すること。
　・整理した内容を自分のような数学未勉強の人に向けて発信すること。
　・オープンな場でフィードバックをもらい、アウトプットの質を高めること。

ⅱ．対象

　・機械学習、ディープラーニングのライブラリの中身を知りたい人
　・高校数学、大学教養数学を忘れてしまった人

ⅲ．参考書籍

　・最短コースでわかる ディープラーニングの数学
　・機械学習のエッセンス
　・マセマキャンパスゼミシリーズ（線形代数、微分積分、確率と統計）
　・見て試してわかる機械学習アルゴリズムの仕組み機械学習図鑑
　・ゼロから作るDeep Learning
　・はじめてのパターン認識
　・生成ディープラーニング

ⅳ．機械学習を学ぶために数学を学ぼうと思った経緯（ポエム）

・自分があこがれているデータサイエンティストやエンジニアは皆「数学を勉強すべき」という意見をもっていたので、自分も数学を勉強しようと思ったから。
（そんなに機械学習の経験があるわけでもないので、長いものに巻かれろ精神で）

・「渋谷駅前で働くデータサイエンティストのブログ」さんの以下の記事を見て、本質的な理解を伴わないAIの技術習得をすると、回りまわって大きな課題へぶつかると考えたから。
　　https://tjo.hatenablog.com/entry/2021/05/14/180344
　本記事は「データサイエンティストになるための」「体系的な勉強」について書かれてはいるが、特に以下の文などについては、自分の中で言語化できていないものが言語化されていたのでとてもすっきりした。

それでもAutoMLなどの出来合いのツールを使うだけなら十分だと思いますが、データサイエンティスト（もしくは機械学習エンジニア）というプロの専門家としてある程度しっかりやっていきたいのであれば、相応に統計学や機械学習の理論やアルゴリズムについてきちんと体系立てて学ぶべきだと個人的には思うのです。その理由は既に述べた通りで、コードを書いて実装するという領域の外側にうまくいかない理由があることが統計分析や機械学習では多いからです。言い換えると「コーディングや実装だけではコントロールできない統計分析や機械学習の『振る舞い』を理解する」べきだ、ということですね。

　・大事なことは、表面的な実装ではなく、体系立てた理論に裏打ちされた実装をしなければならないこと。そして、実装の外側（モデルのふるまいやそれに対する評価手法）ということにもきちんと自分のこだわりをもって想定をしなければならないということだと思った。
　　それができないと、確率的にふるまう機械学習を商用向けに機能化するのはとても難しいんじゃないか。
　そしてそのような実装を目指してアジャイルに活動できるチーム作りが、よりスピーディさを求められるシステム開発現場でAIの機能要件を正しく効果的に実装するために、一番大事なことじゃないかなと考えている。

Ⅴ．数学の勉強内容まとめ

微分・積分

概要

・機械学習、ディープラーニングの学習法の根本原理　＝「損失関数」の値を最小にするためのパラメータ値を見つけること（勾配降下法などのアルゴリズムで）

・アルゴリズムの数学的根拠は微分にある機械学習、ディープラーニングの深い理解には微分が必要

関数について

・「関数」とは：入力値をもとに出力値を導き出す数式のこと。

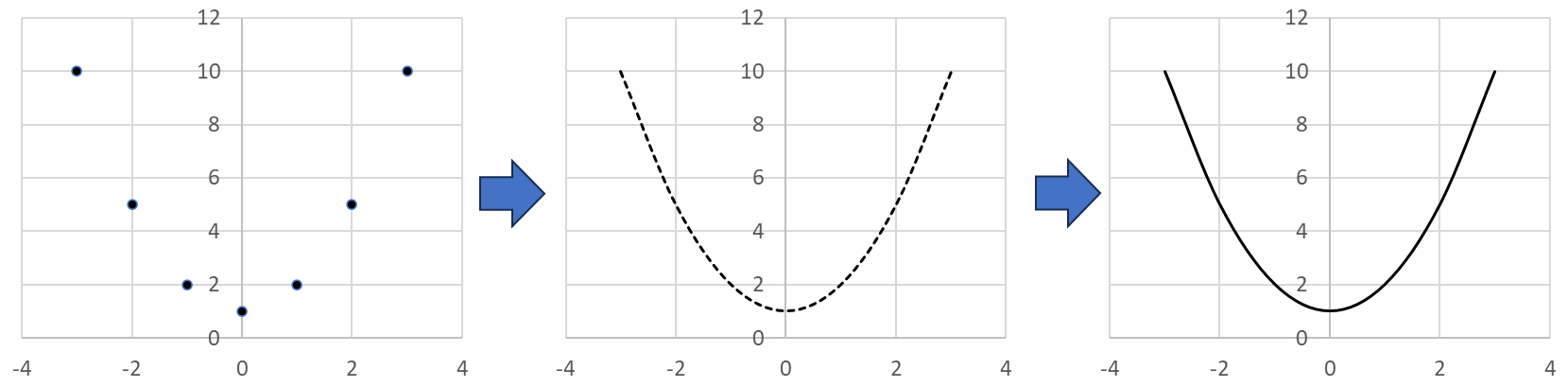
・関数f(x)が与えられると、xに色々な値を代入して、その結果返ってくる関数の値を調べることが可能。

・さらに、xの値をもとに得られたf(x)の出力値をyとして、2次元平面上でどんどんプロットしていくことが可能

・この時、xの間隔をどんどん小さくしていくと、最後は連続的な曲線になる。

合成関数・逆関数

・どちらも関数の派生概念

・合成関数：
　→入力変数と重みのパラメータをかけた結果に対し、ある処理（関数）を施す計算パターン。複雑な関数の理解に役立つ。

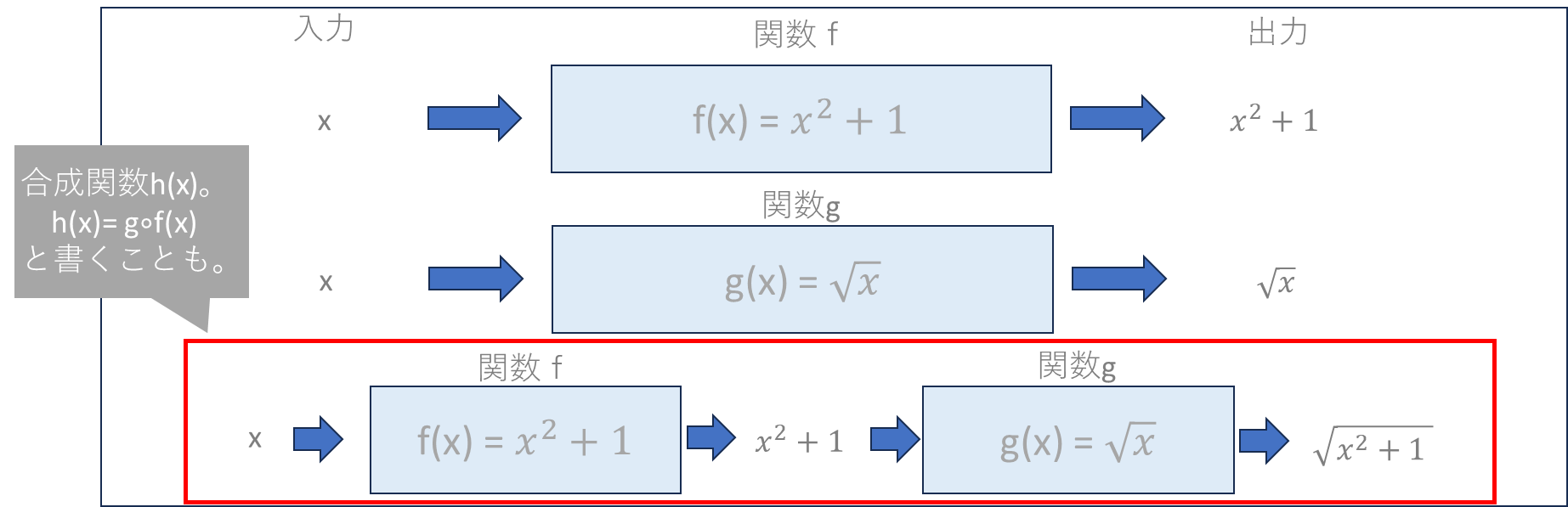
・逆関数：入力＝f(x)の出力、出力＝f(x)の入力、となるような逆向きの結果を出す関数のこと。
　　
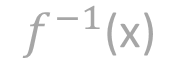
　という表し方をする。

微分と極限

・関数のグラフ上にある点を中心に、グラフを無限に拡大していくとグラフは限りなく直線に近づく。この時の直線の傾きを「微分」という。

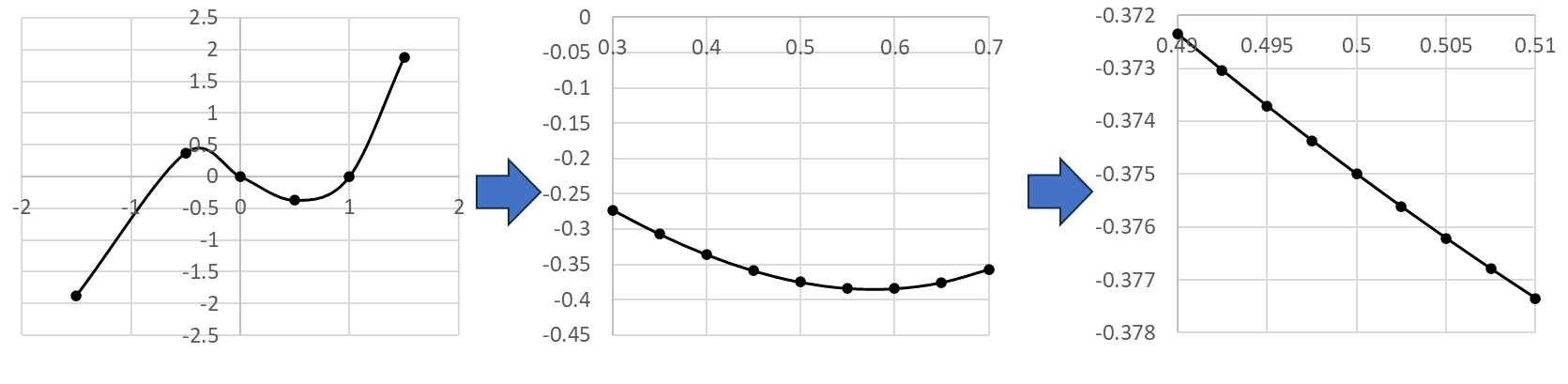
・直線の傾きの値が実際にいくつになるか知るには？
　→この時に使うのが「極限」という考え方。

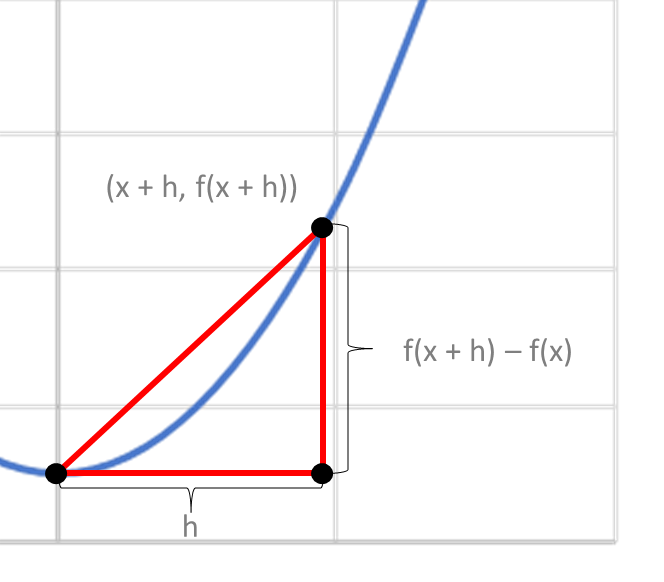
① 上図を見ればわかる通り、グラフ上の２点(x, f(x))と(x + h, f(x + h))を結んだ直線の傾きは、
　
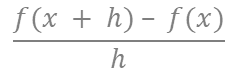
　で表すことができる。
　ここで、無限にhを0に近づけたときの傾きの値が、関数f(x)の微分ということになる。このとき、微分はf’(x)と表す。

② 「無限に近づける」という操作を数学的には「lim」という記号で表す。③ ①②を踏まえて微分の計算をするための式は次のようになる。
　　
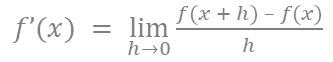
　→これまで使っていた例（f(x) = 𝑥^2 + 1）を使って微分を計算すると、以下の通りになる。

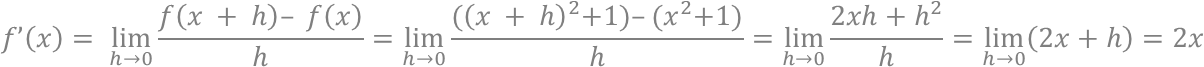
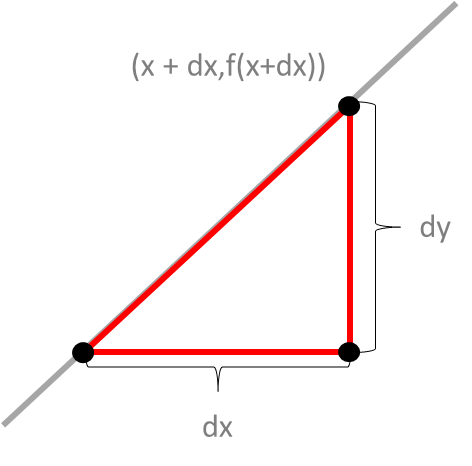
・関数のグラフを無限に拡張して曲線が直線になった状態のとき、
　x → x + dxと微小量だけxの値を増やしたとき、f(x)がどの程度変化するかを見る。
　
・以下の式
　
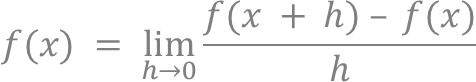
　　の通りであったことを考慮すると、
　　hが無限に小さいとき、f(x + h) – f(x) ≒ hf’(x) となる。
　　Hとdxはともに微小量なので、同じものだと捉えると、
　　dy = f(x + dx) – f(x) ≒ f’(x)dx　という式が成り立つ（らしい）
　　　→関数f(x)において、xの値を微小量dxだけ変化させた場合のf(x)の変化量(f(x+dx)-f(x))は、f’(x)dxに等しい。

・接線の方程式

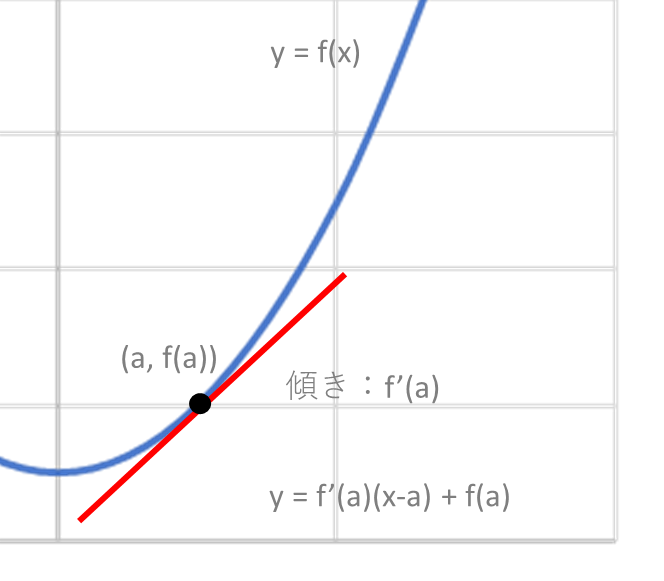
・y = f(x)のグラフ上の点(a ,f(a))でのグラフの接線の傾きはf’(a)となる。
　上記を活用して接戦の方程式を一般化してみる。
　点（p, q）を想定する。この点を通る接線の傾きをmとする。
　接線の方程式は、　　y = m(x - p) + q
　となる。
　この式に、
　　p→a
　　q→f(a)
　　m→f’(a)
　を代入することで、接線の方程式
　　y = f’(a)(x-a) + f(a)
　を作ることができる。

・xの値を微小量dxだけ増やしたときのf(x)の増加値はf’(x)dxに等しくなる。
　→f’(x)の値がちょうど0になる地点ではf(x)の値は増えも減りもしないはず
　→f’(x) = 0となるようなxの地点では、関数の形がちょうど山頂だったり、谷底だったりする。
　　→グラフに応じてそれぞれ「極大」「極小」と呼ばれる

多項式の微分

　に対する微分をすると、以下の公式となる。

・上記の公式の証明は以下の通り。
　・二項定理
　　
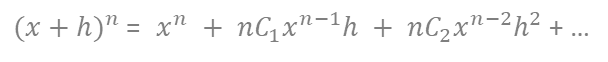
　が成り立つので、
　　
　　
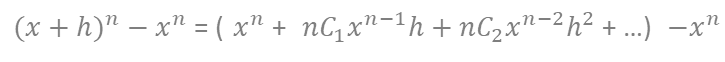
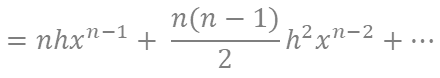
　　よって、
　　
　　
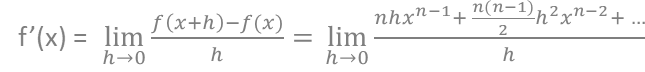
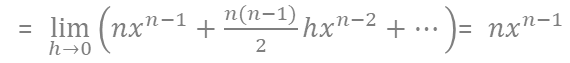
　　つまり
　　

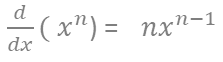
・微分計算の線形性と多項式の微分
　・f(x)とg(x)をxの関数とするとき、pとqを実数として、
　　
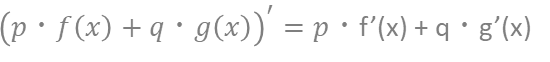
　　が成り立つ。
　　上記のような性質が成り立つことを「線形性」と呼ぶ。
　　→おおざっぱに言うと、「直線っぽい」ということを表している。
　・微分計算の線形性と、先ほど示した

x^n

の微分の公式を合わせると、次のような多項式の微分の公式を作ることができる。
　　
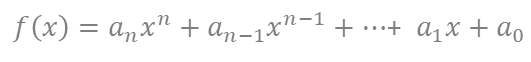
　　とするとき、
　　

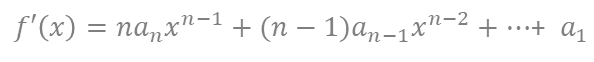
・その他にも以下のような式について微分をやってみる。

　①：以下のように計算してみる。
　　
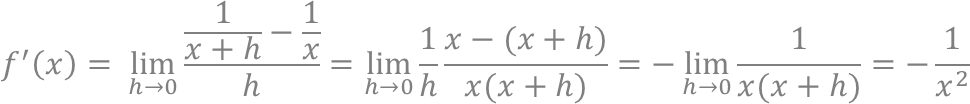
　②：以下のように計算してみる
　　
　　

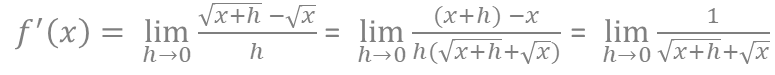
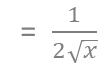
積の微分

・２つの関数f(x),g(x)が与えられているときに2つの関数の積の微分(f(x)g(x))’は、以下の公式となる。
　

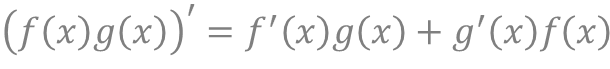
線形代数

　12/21公開予定。

多変数関数の微分

　12/21公開予定。

確率・統計

　近日公開予定。