Processing Advent Calendar 2019 4日目の記事です。遅刻！

※ この記事は連載（の予定）です。前置きや前提知識などを書いたこちらの記事もどうぞ。

はじめに

ジェネ¹といえばランダム、ランダムといえばジェネである（諸説あり）。

座標、大きさ、色、そのほか数値で表せるようなありとあらゆる属性は、作り手が決め打ちしてもいいし、コンピュータ任せでランダムに決めてもいい。結果として、作り手すら予想しなかったような絵や動きができあがる、これはクリエイティブコーディングの醍醐味の一つと言えるでしょう。

日常的にお世話になるものですから、この機会に、
用途に応じた特殊系をいろいろ用意しておくのも悪くないのではないか。
ということで、やっていきましょう。

［備考］
・たいへん地味な内容なので、お暇でない人はとりあえず下の方の作例だけでもどうぞ。
・乱数アルゴリズムとかの話ではありません、簡単な関数をコネコネするだけです。
・この記事では断片的なコードばかり出てきますが、まとまったソースコードは別途公開しています。

よく使う関数を用途別に用意する

JavaScriptに標準で用意されている Math.random() がそうですが、ランダムな値を返してくれる関数というのは、出力値の範囲が 0 以上 1 未満 というのが基本形になります。
短く表記すると [0, 1) です。

実際には任意の範囲でランダムな値が欲しいわけで、[0, 1) の乱数を元に足したり掛けたりして範囲を調整することになります。

p5.js のランダム系の関数

任意の範囲・形式で乱数を作るのを便利にするため、p5.js では次のような関数が用意されています。²
random はよく使ってるのじゃないかしら。

random()         // [0, 1) の範囲でランダムな値を返す
random(max)      // [0, max) の範囲でランダムな値を返す
random(min, max) // [min, max) の範囲でランダムな値を返す
random(array)    // 配列 array の要素をランダムに選ぶ

p5.Vector.random2D() // ランダムな方向の2次元単位ベクトル
p5.Vector.random3D() // ランダムな方向の3次元単位ベクトル

しかしいろいろスケッチを作っていると、もっとあってもいいんじゃないの、と思えてきてしまうのですね。
他にどんなのが考えられるでしょうか。

出力範囲指定系

[0, max) および [min, max)

まず準備運動として、引数の無い random() だけを使い、他の random(max) や random(min, max) にあたる関数を改めて書き直してみましょう。

[0, max) の範囲が欲しいときは、[0, 1) の乱数を max 倍にするだけですね。

/** [0, max) の範囲でランダムな値を返す関数 */
const randomValue = max => random() * max;

これ max が負だったら出力範囲は (max, 0] になっちゃうぞみたいな話は無視します。
なんだこの => は！と思った人は目次記事での簡単な説明、もしくは「アロー関数」で調べるのです。

次に [min, max) の範囲だと、

欲しい値はまず最低でも min 以上である
そこからどのくらい増える余地があるかというと、範囲の長さ、すなわち max - min である

ということで、こうです。

/** [min, max) の範囲でランダムな値を返す関数 */
const randomBetween = (min, max) => min + random() * (max - min);

以下でも、random() だけを使って組み立てていきたいと思います（なぜかは後述）。

ランダムな角度

次に簡単なところで、ランダムな角度が欲しいとき。
[0, 2π) の範囲でよく、これは上記の randomValue の特殊系です。

/** ランダムな角度（ラジアン）を返す関数 */
const randomAngle = () => random() * TWO_PI;

こんなの毎回 random() * TWO_PI とか random(TWO_PI) とか書けば十分では？という感じもしますが、私は大文字で TWO_PI って打つのが面倒なので……。³

ランダムな整数

floor() で整数に直すことができます。
ランダムな整数はそこそこ使うし、毎回 floor() するのは面倒なんではないかしら。
なので、こういうのを作ります。

/** [0, maxInt) の範囲でランダムな整数を返す関数 */
const randomInt = maxInt => floor(random() * maxInt);

[min, max) の範囲のときは、上記の randomBetween と同じ要領です。

/** [minInt, maxInt) の範囲でランダムな整数を返す関数 */
const randomIntBetween = (minInt, maxInt) => minInt + floor(random() * (maxInt - minInt));

ランダムな `true` / `false`

一定の確率で何かをする、というシーンも多いですね。

random() の出力が [0, 1) の範囲で一様という前提なら（実際そうだと思いますが）、
仮に random() < 0.1 とすると、true になる確率は random() の最大値である 1 に対して 0.1、
すなわち 10% です。

これも、それ用の関数を作っておきます。

/** 確率で true か false を返す。`probability` の確率で true */
const randomBool = probability => random() < probability;

// 使うとき
randomBool(0.3) // 30% の確率で true になる

引数として確率を必ず入れるようになっていますが、これをサボりたいとき。
上記の probability を 0.5 とかで直接書き換えちゃっても良いのですが、他の方法としては、

/** `probability` の確率で `true` を返す関数。probability のデフォルト値は 0.5 */
const randomBool = (probability = 0.5) => random() < probability;

のようにデフォルト引数を指定したり、

const randomBool50 = () => randomBool(0.5);
// または
const randomBool50 = randomBool.bind(undefined, 0.5);

のように引数を予約したバージョンを別に作る、なども可能です。
bind については脚注。⁴

ランダムに正 or 負

上記の randomBool の応用で、次のようなものも作れます。

/** 確率で 1 または -1 を返す。`positiveProbability` に入れた確率で正の値になる */
const randomSign = positiveProbability => (random() < positiveProbability ? 1 : -1);

/** `maxMagnitude` を最大の絶対値として、ランダムな正負の値を返す */
const randomSigned = maxMagnitude => (random() < 0.5 ? 1 : -1) * random() * maxMagnitude;

? とか : とかは、目次記事で少し述べた「三項演算子」です。

例えば ±100 の乱数が欲しいなというときに random(-100, 100) みたいにすることが多いですが、これがコードのあちこちに出現して、同じ数字を2回書くのやだなあみたいになってきたときに randomSigned が使えます。

［補足］
この randomSigned で random() を2回やっているのは、後述の応用系と形式を合わせるためですが、
それを気にしない、かつ出力範囲の境界が正負で非対称になるのを気にしなければ、

maxMagnitude => maxMagnitude - 2 * random() * maxMagnitude

の方が効率的ですね。

配列系

ランダムな要素

p5.js で random(array) とするとランダムな要素を取れますが、
再実装してみるとすると、上記の randomInt の要領でインデックスを指定して、こうなるかと思います。

/** 配列 `array` の要素をランダムに取得 */
const randomFromArray = array => array[floor(random() * array.length)];

ランダムな要素を削除

取得と同時に消したい場合があるんですよね。
そういうのが random(array) だとできないので、自分で作ると、こうでしょうか。

/** `array` の要素を1つ、ランダムに削除しつつ抜き取る */
const randomRemoveFromArray = array => array.splice(floor(random() * array.length), 1)[0];

参考： Array.prototype.slice() - JavaScript | MDN

［補足］
同じ配列から何度も削除するなら、p5.js の shuffle とかで shuffle(array) してから array.pop() するとか、いろいろ他にもやりようがあると思います。

重み付きランダム選択（コードありません）

要素ごとに個別に確率を指定した上でランダムに選ぶ。
例えば色をいくつか登録して、60% の確率で赤！ 30% で黄色！とかやるやつ。
一度書いて使ったことがあるんですが、ちょっと時間なくなってきたのでまたにします。
読者諸君の課題とさせていただこう……（理系の教科書でよくあるやつ）

離散系

上記のランダムな整数（randomInt）、
実際には次のように、間隔を指定するために使うケースも多いのではないでしょうか。

const step = 0.25; // 欲しい値の間隔
const result = randomInt(4) * step; // 結果、0, 0.25, 0.5, 0.75 のどれかになる

こういうことを頻繁にやるかどうか次第でもありますが、一応、専用の関数を作ることもできそうです。
randomInt をベースに、step で割ったり掛けたりします。

/** `step` の間隔で [0, 1) の範囲の値を返す */
const randomDiscreteRatio = step => floor(random() / step) * step;

/** `step` の間隔で [0, max) の範囲の値を返す */
const randomDiscreteValue = (step, max) => floor(random() * (max / step)) * step;

"Discrete" は「離散」（値がとびとびであること）の意。

ほか、上の方で作った randomBetween とか randomSigned とか、
いずれも同じ要領で Discrete 版を作れますが省略します。

偏り系

「偏り」の例

乱数はふつう一様ですけど、偏らせたいんだよな～というときがあります。
例えば高確率で 0 に近い値が、低確率で 1 に近い値が出てくる、といった具合です。

これは、今まで作ってきた関数の中の random() の部分に加工を加えることで実現できます。

例えば、p5.js では sq() という、数値を二乗する関数があります。
これを使って、random() の部分を sq(random()) に置き換えると……

random()	sq(random())
0	0
0.25	0.0625
0.5	0.25
0.75	0.5625
1 ⁵	1

どう考えてもグラフでお見せするべきですが、一旦これでご勘弁を！
とりあえず、random() は 50% の確率で結果が 0.5 未満になることを考えると、
sq(random()) の結果は 50% の確率で 0.25 未満になってしまう、
つまり 1 に近い値がなかなか出ない！ということは分かるでしょうか。

一般化

sq() 以外にも任意の関数が使えると、どう偏らせるかを好きに操作できることになります。
そこで sq(random()) を一般化し、sq のところになんでも入れられるようにしたい。
目次記事で少し触れた、コールバック関数の出番です。

/** `random()` の結果を、任意の関数 `curve` で偏らせたうえで返す */
const randomRatioCurved = curve => curve(random());

// 例えば
randomRatioCurved(sq) // 関数 sq の曲線に従い、比較的高確率で 0 に近い値を、低確率で 1 に近い値を返す
randomRatioCurved(x => Math.pow(x, 5)) // 5乗するので、sq よりもずっと強く 0 側に偏る

最適なネーミングかどうかちょっと分かりませんが、sq() とかはグラフ上で曲線になるので、そういうのを入れる部分の引数を curve と名付けています。

バリエーション

この要領で、上で作ってきたような関数群の Curved 版を。

const randomValueCurved = (curve, magnitude) => curve(random()) * magnitude;
const randomBetweenCurved: (curve, start, end) => start + curve(random()) * (end - start);

こいつらが何をしてくれる関数なのか、を日本語で短く言うの難しいですね。

curve に入れる関数として基本的に想定しているのは、
「入力値の範囲が [0, 1) なら出力値の範囲も [0, 1) である」
ような関数です（sq() をはじめ冪乗系はこれに該当します）。
このようなとき、

randomValueCurved() の結果は 0 以上 magnitude 未満
randomBetweenCurved() の結果は start 以上 end 未満

であることが約束されます。
が、curve の内容によってはその限りでないし、でも意図した通りに動くなら別に何でも良いので、なんというか、使い方次第です。

名前空間を整理して再利用できるようにする

いろんな関数を作ってしまいました。
これらをいつでも再利用できるようにまとめておきたいわけですが……

※ ここからさらに情報の誰得感が増してくるので、関心薄ければ読み飛ばしてください

どうやって再利用するか

個別の関数を都度コピペするような使い方だと、そもそもそこまで劇的に便利な関数じゃないし、目的の関数を探してコピペするより、その場その場で適当に書いたほうが楽かもしれませんね。

では、関数をズラッと並べたファイルを用意しておいて、そのファイルごと毎回使い回そうか。それもできますが、名前の衝突とかの心配があって、あんまりグローバル空間にたくさんの名前を置いときたくない。

そこで、一つの巨大なオブジェクトにまとめる方法があります。

オブジェクトにまとめる

const Random = {
  value: max => random() * max,                        // 上の方で randomValue() だったやつ
  between: (min, max) => min + random() * (max - min), // 上の方で randomBetween() だったやつ
  angle: () => random() * TWO_PI,                      // 上の方で randomAngle() だったやつ
  // ...
};

// 使うとき
const myValue = Random.value(10);
const myAngle = Random.angle();

こうすると、Random という名前が使用済みでさえなければ、この Random オブジェクトをまるごと使いまわすことができそうです。⁶

さらにまとめる

上の方で作った関数の中には、randomBetweenCurved みたいに長めの名前もあったし、改造したらもっと長いのもできるかもしれません。
そこで、Random オブジェクトの中身をもっと整理してみます。

const Random = {
  value: max => random() * max,
  between: (min, max) => min + random() * (max - min),
  angle: () => random() * TWO_PI,
  // ...
  Integer: {
    value: maxInt => floor(random() * maxInt), // 上の方で randomInt() だったやつ
    // ...
  },
  Discrete: {
    ratio: step => floor(random() / step) * step,  // 上の方で randomDiscreteRatio() だったやつ
    // ...
  },
  Curved: {
    // ...
  }
};

// 使うとき
const myInt = Random.Integer.between(10, 20);

特定のテーマでまとめられそうな関数群は、さらに別のオブジェクトでまとめて、入れ子状にする。
いろんな関数があると、区別するために一つ一つの名前が必然的に長くなりますが、こうして整理すると短くできます。

まあ、あくまで一例だと思っていただければ。

任意の関数を `random()` として使えるようにする

人によって需要は違うので、もういいやという人はこのへんでやめても良いのですが、
ここでは、オブジェクト方式からさらに進める方法も見てみます。

なにがしたいのか

後出し情報ですみませんが、なぜこの記事で random() だけをベースにいろんな関数を作ったかというと、ベースとして使う関数を好きに選べるようにしたかったからです。
「[0, 1) の範囲で乱数を出すような関数」を好きに選んできて、それを元に、上述の関数群を一気に用意できるようにしたい。

そのような関数として、いまのところとりわけ簡単に使えるものとしては

p5.js の random
標準の Math.random

があります。

この記事で今まで前提にしてきた p5.js の random は、
randomSeed() とかでシードを変えられたりするメリットがありますが、一方では

random の内部で毎回条件分岐してて気分的にちょっとイヤン
（ふつう気にする必要ないけど、一応公式でも触れられている：Optimizing p5.js Code for Performance）
setup draw の中から呼ばないと使えなくなっちゃう

とかのデメリットがあります。

なので私の場合だと Math.random とかを使いたい。⁷

全体を関数で包む

つまり、こうだ。

/**
 * いろんなランダム関数をひとまとめにしたオブジェクトを返す。
 * 引数の `random` は、[0, 1) の乱数を返す任意の関数。デフォルトは `Math.random`。
 */
const createRandomFunctions = (random = Math.random) => {
  return {
    value: max => random() * max,
    between: (min, max) => min + random() * (max - min),
    // ...
  };
};

前章の Random オブジェクトにあたる巨大オブジェクトを、createRandomFunctions の中で作成して返すようにしています。

使うときはこうです。

const Random = createRandomFunctions(); // 最初に用意しておく

const myValue = Random.value(10); // 都度、使いたい関数を使う

結果

以上でいろいろ整ったのではないでしょうか、
出来上がったコードがこちらです（この記事では省略したような関数も一応揃えています）。
https://github.com/fal-works/p5js-snippets/blob/master/random/random.js

めでたしめでたし（ほんとか？）

作例

以上が枕でありまして、じゃあ何か描いてみましょうか、ということで作例です。

1. 各種関数の可視化

作ってきたうちの一部の関数だけですが（Discrete系とかまるまる抜けている）、
数直線上にプロットしてみました。
Curved系は5乗とかしているので左側に出る確率が高いな、とかがわかります。

動くやつ ▶ https://fal-works.github.io/p5js-snippets/random/example-1/

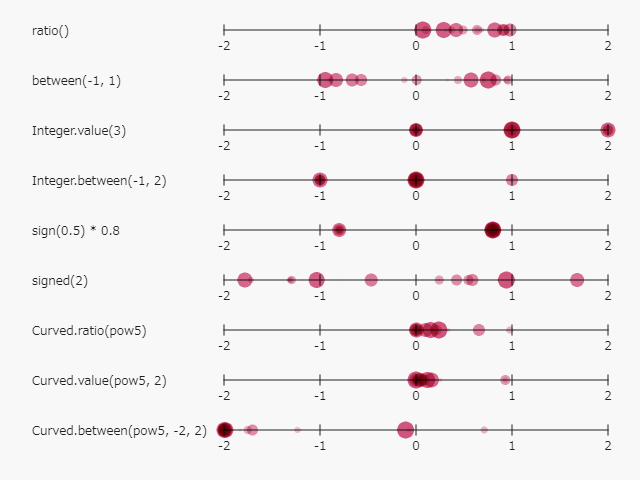
なんの意味も持たない数値データですが、
プロットして可視化してフニフニ動かすと、なぜか愛着が湧いてくる気がします。

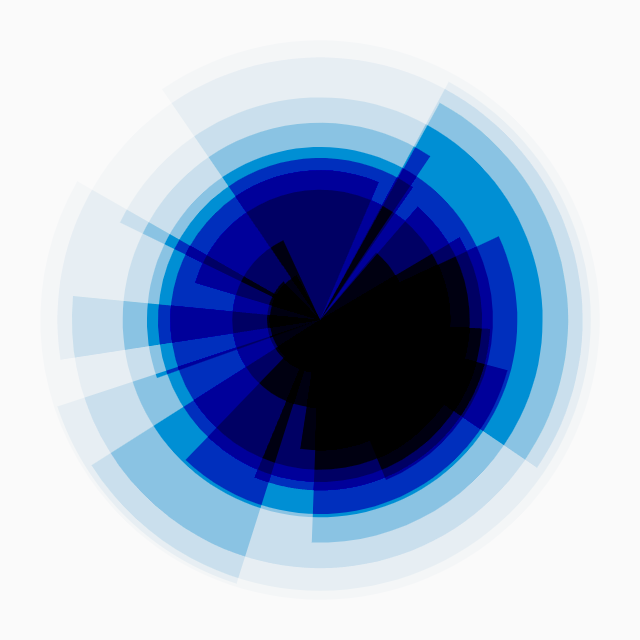
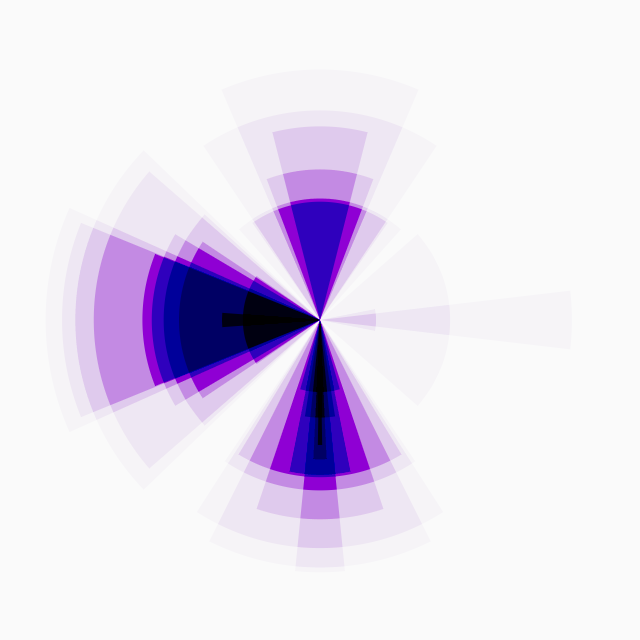
2. 絵作りに応用

簡単なところで、「ランダムな角度と大きさで描いた扇形を重ねる」というのをやってみましょう。
（ここで大きさというのは中心からの距離の意です）

動かせるやつ ▶ https://fal-works.github.io/p5js-snippets/random/example-2/

せっかく作った関数群がどんな効果をもたらすかを見てみたかったので、
default, discrete, fan, curved の4つのモードをラジオボタンで選べるようになっています。

default

なんの工夫もないたんなるランダム。

ササッと作った割には、個人的に結構好きです。
いやーもうこれでいいんじゃないでしょうか。満足。

discrete

用意した Discrete 系の関数を使って、大きさおよび角度のランダム値をとびとびにしたバージョンです。

お！これもちょっとオシャレなんじゃないの。
離散的なランダムはもっといろいろ使いどころがありそうですね。

fan

扇が向く方角を、上下左右の4方向に縛って離散的ランダム。
扇の広さは、お隣のエリアに重ならない程度の範囲で普通のランダム。
扇の大きさも普通のランダムです。

ホホウ！（変なテンションになりつつある）

curved

用意した Curved 系の関数を使い、
大きさについては2乗する関数で、扇の広さは4乗する関数で 0 側に偏らせる。
扇の方角は単にランダムな角度。

アーハーン？
一目瞭然というほどではないかもしれませんが、これを見てから default のやつを見直すと、default のほうがなんというかまんべんなく値が散った感があり（実際そのはずですが）、curved のほうがエッジが効いてる（？）感があります。

なにか変化がほしいときにこうして確率を不均等にするのは有効だという気がします。

まとめ

いろんなランダム関連の関数を用途別に揃える
再利用に向けて整理する
実際に使って絵を描いてみる

ということをやってきました。

ソースコード：　　 https://github.com/fal-works/p5js-snippets/tree/master/random
作例まとめページ： https://fal-works.github.io/p5js-snippets/random/

困ったことに（嬉しいことに？）ランダム関連の話題はまだあるんですよね。
これとか。　乱数にコクを出す方法について - Togetter
これはまたネタにするかもしれないし、しないかもしれないです。

以上、見ていただきありがとうございました。

generative art ↩
ちなみに p5.js の random(min, max) は、実際に入れた値が min > max だったときにはよろしく入れ替えてくれるみたいなんですが、そういうのはこの記事では気にしないこととします。 ↩
いろいろ蛇足を書くと、まず TAU というのがあるけどあんまり使われてないっぽい。angleMode(DEGREES); で360度モードにできるけど、標準の Math.sin() とかはラジアンのみなのもあって、私はあまり使う習慣がない。あと、 random や TWO_PI を含め p5.js 独自の関数・変数は setup や draw の中からでないと使うことができず、任意の場所でランダムな角度が欲しいときに Math.random() * 2 * Math.PI とか毎回書いてられないのでやっぱり用意しときたい、という動機もあります。 ↩
bind で引数を予約した新たな関数を作れます。bind の第一引数は、対象の関数の中で this を参照したときに使われる値となるのですが、今回の randomBool で this は登場しないので、ここでは何も入れたくないため undefined としています。bind の第二引数以降に入れた値が、対象の関数の第一引数以降に入る、というふうに一つずれた感じになるので注意。参考： Function.prototype.bind() - JavaScript | MDN ↩
厳密には 1 自体は範囲外 ↩
ES2015 や TypeScript の import / export を使う場合は、import * as Random from ... とかして名前をつけられるので、わざわざオブジェクトにまとめる必要はないです。 ↩
ちなみに Math.random の方のデメリットとしては乱数の質が悪いということが言われていて、乱数に質も何もあるのかしらと思うかもですが、これが、あるんですね。（これだけだとあまりわからないですが参考：疑似乱数 - Wikipedia）……この先は詳しくないのですが、乱数のアルゴリズムというのはいろいろあるので、人によってはさらに別の関数を採用する動機があるかもしれません。 ↩

p5.js向け 有用無用道具箱 - ランダム編