目次
確率変数とは
確率変数とは、取り得る値の範囲は分かっているが、どれになるかは分からない値を確率変数といいます。
たとえば、サイコロを振った時、出る目は1,2,3,4,5,6のいずれかになりますが、この1から6までの目が、確率変数となります。
式で書くと、以下になります。
P(X) = \frac{1}{6} (X = 1, 2, 3, 4, 5, 6)
また、さいころを投げて5の目が出る事象の確率は、以下の式で表すことができます。
P(5) = \frac{1}{6}
確率分布
確率分布とは、確率変数のそれぞれ値と、その値が出現する確率の分布のことです。
例えば、サイコロの例でいうと、以下のようなものになります。
| サイコロの目 | 確率 |
|---|---|
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
離散型確率変数
離散型確率変数とは、とびとびの値しか取らない確率変数のことを指します。
例えば、サイコロの目は、1の次は2であり、1.1や1.2は存在しません。
このような変数を離散型確率変数といいます。
身長や体重のようなものは、連続型の確率変数になります。
離散確率分布
離散型確率変数の確率分布を、離散確率分布といいます。
確率質量関数
離散確率変数がxとなる確率をf(x)としたとき、このf(x)のことを、確率質量関数と言います。
また、全事象が起こる確率は1であることから、以下の式が成り立ちます。
\Sigma_{i=1}^{n} P(x_i) = P(x_1) + P(x_2) + ・・・ + P(x_i) = 1
サイコロの例であれば、以下のようになります。
\frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = 1
連続型確率分布
連続型確率変数とは、前述の離散型確率変数の逆で、身長や体重の様に、隣合う値の間に、無数に値があるものです。
例えば、身長の場合であれば、180cmと181cmの間には、180.01cm, 180,001cm, 180.0001cm・・・のように、無数に値があります。
このような連続型確率変数の確率分布のことを、連続型確率分布といいます。
連続型確率変数の範囲を1から6までとしたとき、3が出る確率は、離散型の場合の様に、1/6にはなりません。3は、無限に存在する値のうちの一つであり、この場合の確率は0`になります。
P(x) = \frac{1}{\infty} = 0
確率密度関数
連続型確率変数の場合、特定の確率変数の値のとる確率は0になってしまいますが、
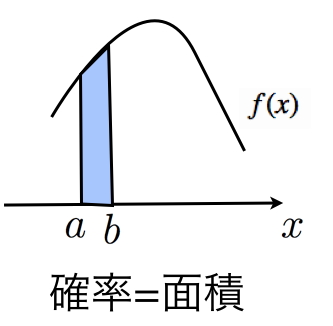
連続型の変数Xが、a≤X≤b となる確率を、確率密度といいます。
連続型確率変数Xがa以上b以下となる確率が以下で求められるとき、f(x)を確率密度関数といいます。
全事象の確率の合計は1となるため、= 1となっています。逆に、1にならないものは確率密度関数ではありません。
P(a \leq X \leq b) = \int _a ^b f(x) dx = 1
この式では、以下の図のように、aからbの範囲の面積を算出しています。
f(x)をaからbで定積分した値が、Xがaとbの間にある確率を表します。
引用元:高校数学の美しい物語