はじめに
ドローンやセグウェイが登場してからというもの,それらを操る為の制御技術,「制御工学」を目にすることが多くなった.
しかし同時に「抽象度が高い「制御工学」は分かりにくい.特に数式だらけの現代制御は何がしたいのか分からない」という声も聞こえてきた.
そこで筆者が学んだ現代制御の考え方を備忘録としてまとめることで,誰かの助けになるかも知れないと思いこれを記す.
状態空間表現
現代制御を勉強しようとすると,いきなり出てくる次式
\left\{
\begin{align}
\dot{x} &= Ax + Bu\\
y &= C^{\mathrm{T}}x
\end{align}
\right.
上式を状態方程式,下式を出力方程式と言い,この表現法を状態空間表現と呼ぶらしい.
無条件でこの状態空間表現を信じて現代制御を勉強するが,結局この表現がいまいちピンと来ない.
状態空間表現には一体どんな旨味があるのだろう.
そもそも状態空間って?
参考文献では状態空間を次のように定義している.
$n$個の状態変数を要素に持つ$n$次元空間は状態空間と呼ばれる
なるほど,フワっとしていて分からない.
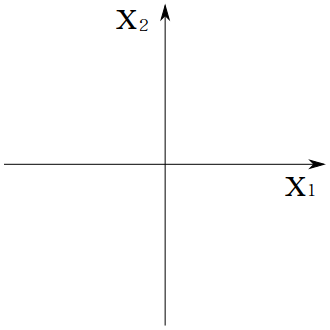
とりあえず$n = 2$としてみると
2個の状態変数を要素に持つ2次元空間は状態空間と呼ばれる
これならなんとか分かりそう.
2個の状態変数とは,とりあえず「状態」の変数が2個あるのだろう.
2次元空間とは平面のことだろう.
つまり「状態」とやらの変数が2個ある時,この変数らが張る平面を状態空間と呼ぶのだ.
ならば1つ目の状態変数を$x_1$,2つ目を$x_2$とすると図に示す平面が状態空間となるはずだ.
なるほど,状態空間は何となく理解できた.しかし肝心の「状態」が分からない.
状態
参考文献では状態を次のように定義している.
動的システムの状態 {$x_1(t),x_2(t),...,x_n(t)$} は, $t = t_0$の初期状態と
$t\geq t_0$の入力 {$u_1(t),u_2(t),...,u_m(t)$} から$t\geq t_0$のシステムの振る舞いを
完全に決める最小の集合である
また,この集合の要素 {$x_1$}, {$x_2$}, $...$, {$x_n$}は状態変数と呼ばれる
なるほど,分からない.
一つ一つバラしていこう.
どうやら「状態」とは「動的システムの状態」らしい.
また「状態」は $t = t_0$の初期状態と,以降 $t\geq t_0$の入力が分かっている時,システムの振る舞いを完全に決めるようだ.
つまりシステムの振る舞いが「状態」によって記述される.
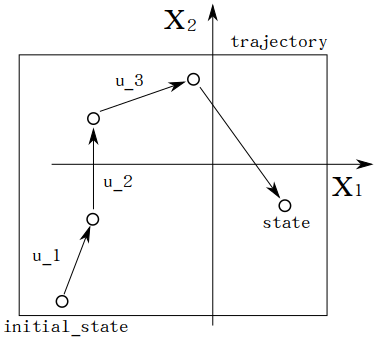
初期状態をスタート地点,以降の入力を逐次の指令だと考えると,
「スタート地点と逐次の指令が分かっている時,システムの振る舞いが完璧に分かる」
と言い換えられる.
この時システムの振る舞いは状態空間の軌跡で表され,「状態」はある時点での状態空間の点だと言えそうだ.
例題
実際に例を挙げて考えてみる.
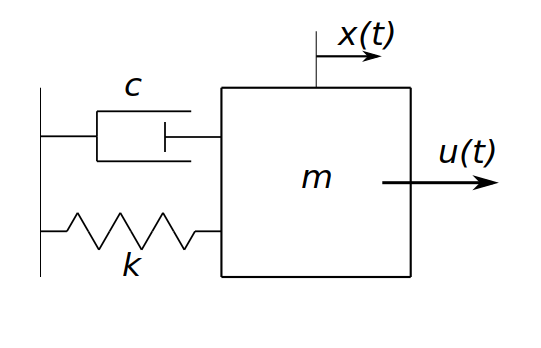
上に示すマス-バネ-ダンパモデルは次式の様に記述できる.
m\ddot{x}(t) + c\dot{x}(t) + kx(t) = u(t) \tag{1}
このシステムに状態を定義しよう.
状態はシステムの振る舞いを完全に決める最小の集合だから,集合の要素である状態変数の最小の組み合わせを考える必要がある.
このシステムは,加速度 $\ddot{x}(t),$速度 $\dot{x}(t),$位置 $x(t)$ の3変数で構成されているため3つの状態変数が必要そうだが,3つは本当に最小だろうか.
3変数をよく観察すると,$\dot{x}(t) = \frac{d}{dt}x(t)$, $\ddot{x}(t) = \frac{d}{dt}\dot{x}(t)$ の関係が見えてくる.
ここで $x(t) = x_1(t),\dot{x}(t) = x_2(t)$と置いてみる.
すると3変数は
\left\{
\begin{align}
x(t) = x_1(t)\\
\dot{x}(t) = x_2(t)\\
\ddot{x}(t) = \dot{x_2}(t)
\end{align}
\right.
と書くことができる.
これをシステム(1)に代入し,まとめると
\begin{align}
&\dot{x_1}(t) = \dot{x}(t) = x_2(t)\\
m\dot{x_2}(t) &+ cx_2(t) + kx_1(t) = u(t)
\end{align}
上式の様に新たなシステムが得られる.
これを次のように整理することでシステム(2)を得る.
\begin{align}
&\dot{x_1} = x_2\\
\dot{x_2} = -&\frac{c}{m}x_2 -\frac{k}{m}x_1 + \frac{1}{m}u
\end{align}
\tag{2}
少し複雑な式変形を行ったが,結果的にシステム(1)はシステム(2)の様に表記できた.
システム(2)を見ると,3変数で記述されていたシステム(1)が2つの状態変数 $x_1,x_2$で記述されている.
これより,システム(1)の振る舞いを完全に記述するための状態変数は2つでよさそうだ.
なのでシステム(1)の状態は {$x_1,x_2$}と定義するべきだろう.
ところで,どうして必要な状態変数の数が3つから2つへと減ったのだろうか.
よくよく考えてみると $x(t) = x_1(t),\dot{x}(t) = x_2(t)$と置いたからではないだろうか?
まさしくその通りで,$x(t) = x_1(t),\dot{x}(t) = x_2(t)$ と置いたのは状態変数{ $x_1$},{ $x_2$}を定義する事と同じである.
上記の様に「状態」として,ある状態変数とその微分値を用いることで必要な状態変数を減らすことができる.
では状態変数はどのように選ぶべきなのか.
状態変数の選び方
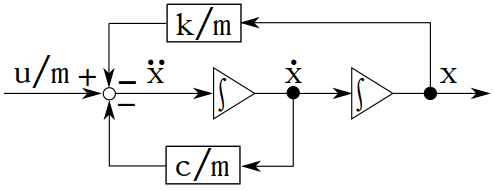
結論から言うと,状態変数にはシステムの積分器の出力を選ぶべきである.
上図を $\ddot{x}$について解くと
\ddot{x} = -\frac{c}{m}\dot{x} -\frac{k}{m}x + \frac{1}{m}u \tag{3}
上式(3)を得,ここでシステム(1)の積分器の出力 $x(t)$, $\dot{x}(t)$を状態変数として次式
\left\{
\begin{align}
x_1 = x\\
x_2 = \dot{x}
\end{align}
\right.
の様に定義し,式(3)を状態変数で表現すると
\dot{x_2} = -\frac{c}{m}x_2 - \frac{k}{m}x_1 + \frac{1}{m}u
を得る.これはシステム(2)と同じであることから,状態変数にはシステムの積分器の出力を選べば良いことが確認できる.
まとめ
今回の記事では状態空間とそれを構成する状態及び状態変数,状態変数の選び方をまとめた.
次回はそれらを用いた状態方程式,動的システム,シミュレーション等をまとめたい.
参考文献
- S. M. Tripathi "MODERN CONTROL SYSTEMS : An Introduction"