颯式
颯式(はやてしき)は、「クイックソート種より高速」を目指した、マージソートの改良アルゴリズムです。
以下の特徴があります。
- 比較ソート
- 安定ソート
- 外部領域:N
- 最良:O(N)
- 平均:O(N log N)
- 最悪:O(N log N)
- 再帰:無し
リポジトリ
基本となるアルゴリズム
- 外部領域を、2Nの連続帯として見立てます。
- 値を外部領域に置く際、以下のルールを適用します。
- (最大値 ≦ 値)であれば、昇順列の上側に置き、最大値を更新します。
- (値 < 最小値)であれば、降順列の下側に置き、最小値を更新します。
- (最小値 ≦ 値 < 最大値)であれば、新しい値(最大値であり最小値)を昇順列に置き、それまでに並べた値群をPartとします。
- Part群をマージします。
具体的な流れ
外部領域を、2Nの連続帯として見立てます
4 5 1 2 7 6 3 8|入力列
. . . . . . . .|外部領域
→昇順列 降順列←|実際
|4 5 1 2 7 6 3 8|入力列
. . . . . . . . . . . . . . . .|外部領域
降順列←|→昇順列 |2N見立て
新しい値(最大値であり最小値)を昇順列に置く
|. 5 1 2 7 6 3 8
. . . . . . . . 4 . . . . . . .
次の値は(最大値 ≦ 値)なので、昇順列の上側に置き、最大値を更新
|. . 1 2 7 6 3 8
. . . . . . . . 4 5 . . . . . .
次の値は(値 < 最小値)なので、降順列の下側に置き、最小値を更新
|. . . 2 7 6 3 8
. . . . . . . 1 4 5 . . . . . .
次の値は(最小値 ≦ 値 < 最大値)なので、新しい値(最大値であり最小値)を昇順列に置く(Part:145が完成)
|. . . . 7 6 3 8
. . . . . . .|1 4 5|2 . . . . .
次の値は(最大値 ≦ 値)なので、昇順列の上側に置き、最大値を更新
|. . . . . 6 3 8
. . . . . . .|1 4 5|2 7 . . . .
次の値は(最小値 ≦ 値 < 最大値)なので、新しい値(最大値であり最小値)を昇順列に置く(Part:27が完成)
|. . . . . . 3 8
. . . . . . .|1 4 5|2 7|6 . . .
次の値は(値 < 最小値)なので、降順列の下側に置き、最小値を更新
|. . . . . . . 8
. . . . . . 3|1 4 5|2 7|6 . . .
次の値は(最大値 ≦ 値)なので、昇順列の上側に置く(Part:368が完成)
|. . . . . . . .
. . . . . .|3|1 4 5|2 7|6 8|. .
最終的な外部領域
4 5|2 7|6 8|. . 昇順列見立て
. . . . . .|3|1 降順列見立て
4 5|2 7|6 8|3|1 実際の内容
生成したPart群をマージします
145 27 368
12457 368
12345678
ソート完了
改良
基本アルゴリズムから更に、以下の改良を施します。
- Partの長さを確保する為、インサートソートを行います。
- 再帰をしないように、逐次マージを行います。
検証を行った環境
- Windows 10 Pro 64bit
- Core i7-8700 3.20GHz
- Microsoft(R) C/C++ Optimizing Compiler Version 19.16.27030.1 for x64
- clang version 8.0.0 (tags/RELEASE_800/final)
- gcc version 8.3.0 (Rev2, Built by MSYS2 project)
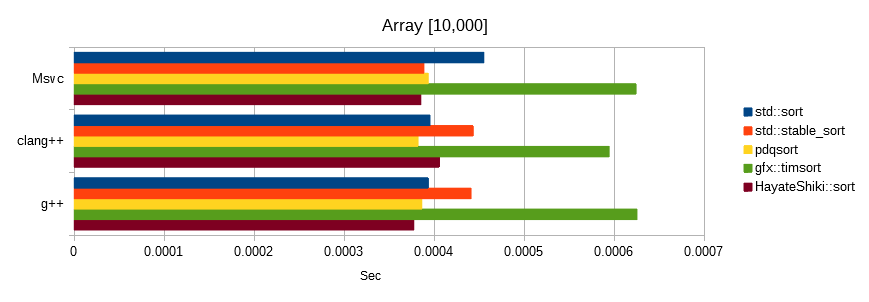
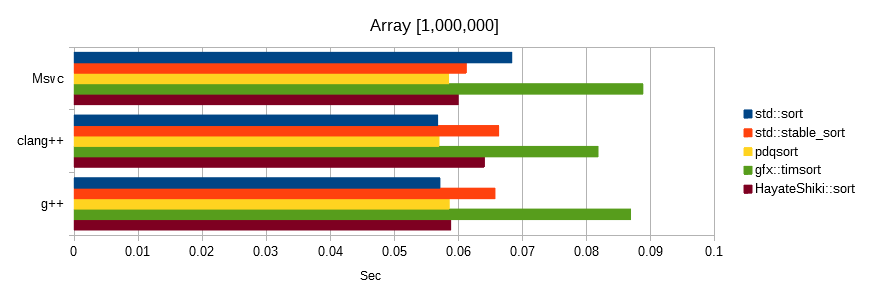
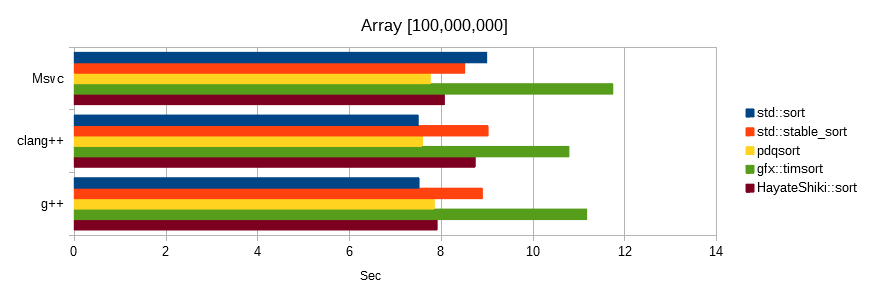
乱数ベンチマーク
同じシードから生成したfloat値をソートしました。
単位は秒で、数値が低いほど高速です。
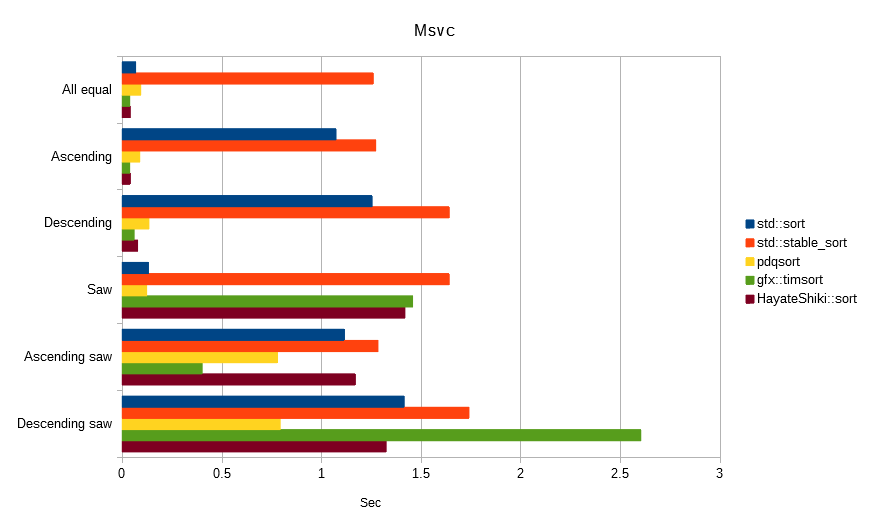
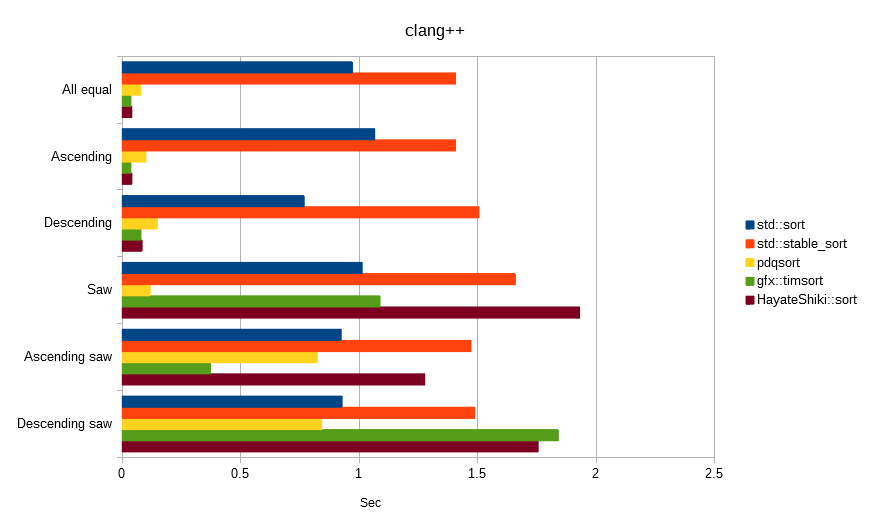
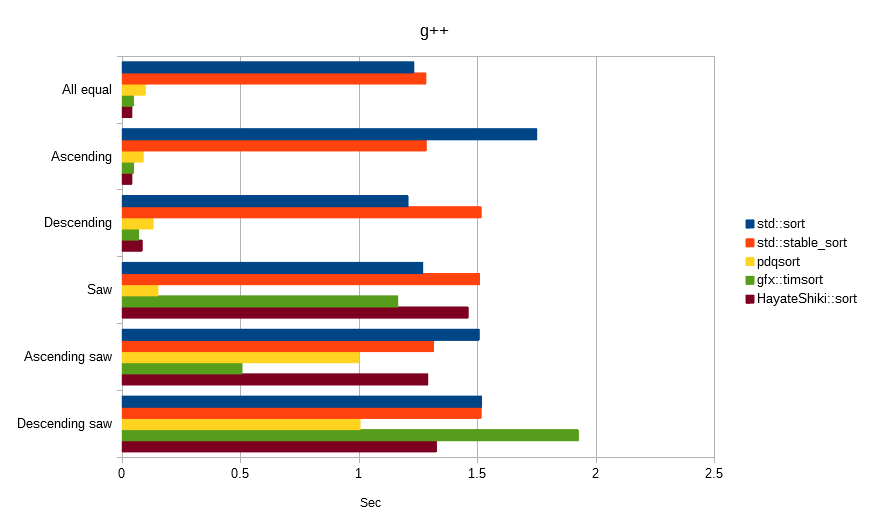
特性ベンチマーク
以下は全て、float値「100,000,000」件でソートしました。
単位は秒で、数値が低いほど高速です。
余談
如何だったでしょうか?
颯式は、安定ソートでありながら、乱数に強いことが窺えます。
特性ベンチマークでは、アルゴリズム特性ではなく、コンパイラの最適化特性の影響が強く出てしまう為、ほとんど判断材料にならないことが分かりました。
マージソート種がクイックソート種に勝てる日は来るのでしょうか?
ソートアルゴリズムには、まだ浪漫が残っています。
以下の記事も併せて読んでいただけると、より楽しめるかも知れません。