BlenderとPythonでラクラクモデリング

#前書き
Blenderは無料なうえにとてもたくさんの機能が存在するので初見殺しとよく言われていますモデリングをするのに持ってこいのソフトです!
とは言えいきなりたくさんの機能を使ってモデリングしようにも何からやればいいかわかんないですよね…
#そこで!
今回はたった一つの機能を使ってモデリングしていこうと思います。

#それは…
**「Pythonが書ける」**機能です!今回はこれを使っていろんなことをしていこうと思います。頭悪い
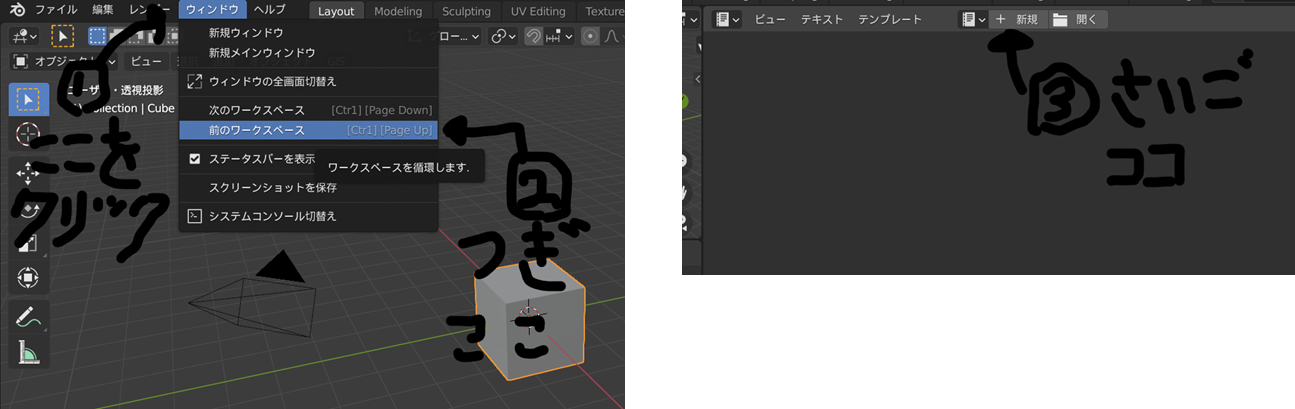
#環境設定
ここはさらっと説明します。

ね!簡単でしょ

あっインストールはここです。
https://www.blender.org/

ではここからはいろんなものを作っていこうと思います

#プレステ2の起動時に出てくるやつ
いったい何のことって思う人もいるかもせれませんが…

こんな感じのやつです

import bpy
import random

for i in range(30):
    for j in range(30):
        bpy.ops.mesh.primitive_cube_add(location=(i-15,j-15,0),scale=(1,1,random.randint(1,10)))

こんな感じになります

#某・〇・リング

上のようなドーナッツを作っていきましょう

import bpy
import math

for i in range(8):
    bpy.ops.mesh.primitive_uv_sphere_add(location=(2*math.cos(math.pi*i/4),2*math.sin(math.pi*i/4),0))

location=(x座標,y座標,z座標)のx座標とy座標にcosとsinを代入しました。
要するに円周上に球を八個等間隔に並べたってことです。
これでポンッ…某リングが完成しました。

#グラフ(線)
今度はグラフを作りましょう。

import bpy
import math

for i in range(180):
    bpy.ops.mesh.primitive_cube_add(location=(i,10*(math.pow(math.log(0.05*i+1)+math.sin(math.pi*i/30),3))*math.cos(math.pi*i/90),10*(math.pow(math.log(0.05*i+1)+math.sin(math.pi*i/30),3))*math.sin(math.pi*i/90)))

今回は$10\times log_e(0.05\times x+1)+\sin({x\pi/30})$という極形式を縦軸成分と横軸成分に分解してθを媒介変数としたグラフになっております

ちなみにこんな感じのグラフになります。

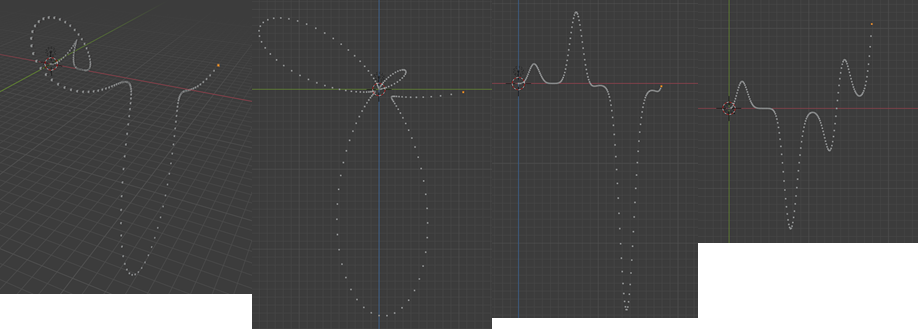
全体図と各軸から見た図

このソースコードどっかで見たことがあるって?君のような勘のいいガキは嫌いだよ

#グラフ(平面)
さて次はこれを平面にしましょう。

import bpy
import math

for i in range(30):
    for j in range(20):
        bpy.ops.mesh.primitive_cube_add(location=(i,20-j+10*(math.pow(math.log(0.05*i+1)+math.sin(math.pi*i/30),3))*math.cos(math.pi*i/90),j+10*(math.pow(math.log(0.05*i+1)+math.sin(math.pi*i/30),3))*math.sin(math.pi*i/90)))

先程の式の横軸に等間隔に並べ縦軸はキューブ同士の間隔を少し開けました。
なおこんな感じのグラフになります。

#終わりに
今回はPythonで簡単にモデリングする方法をいろいろ書きました。他にもいろんなことに使えるので是非やってみてくださいね!