Pythonで確率プロット
目的
よく業務で使用しているPythonを用いた確率プロットの作成方法について紹介したい。
(検索しても良い情報がなかったので…)
参考: 正規確率プロット(Normal Q-Q Plot)の作成 with Excel
こちらはExcelで確率プロットを作成しているページ。
本記事で紹介しているのは、ほぼこちらのPython版となる。
確率プロットとは
QQ-Plotとも言う。
簡単に言えば、データが正規分布に即しているかどうかを視覚的に判断できるようにしたもの。
正規分布から外れているデータを発見したり、近似の直線を引くことで、データがどのくらいの範囲に収まるかを予測したりする。
正規分布に関しては以下の書籍がわかりやすくて勉強になる。
講談社
売り上げランキング: 82,727
環境について
GoogleColaboratryのPython3ノートブックで作成した。
JupyterNotebookでも使えると思う。
コード
使用するライブラリをimport
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
ndarrayとDataFrameでデータを用意する
今回はサンプル用に正規分布に則ったデータを作成する。実際の業務ではcsvファイルから読み込んだりすることになる。
使用しやすいようにndarrayとdataframeの両方で用意する。
また、列数と行数を確保しておく。
# 正規分布のデータを3つ作成
npspl = np.random.normal(50, 10, [500, 3])
rownum, colnum = npspl.shape[0], npspl.shape[1]
dfspl = pd.DataFrame(npspl, columns=['Data1','Data2','Data3'])
ヒストグラムプロット
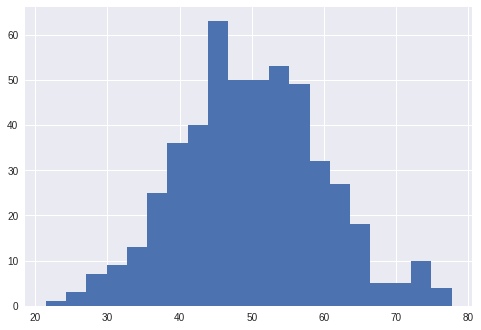
データが正規分布であることを確認するためヒストグラムをプロットしてみる。
for i in range(colnum):
plt.hist(npspl[:,i], 20)
plt.show()
以下のように出力される。
パーセンタイル順位を作成、Normsinvに変換する
ここが確率プロットのポイント。
- パーセンタイル順位とは?
順位をパーセントに変換したもの。
例えば、とある値が全体の上位20%の大きさだったらパーセンタイル順位は0.8となる。
- Normsinvとは?
標準正規分布における期待値で、パーセンタイル順位から算出する。
norspl = stats.norm.ppf((
np.array(dfspl.rank(method='first', na_option='keep') - 1/2)/ rownum),
loc=0, scale=1)
ワンライナーで書いちゃったので分解して解説する。
以下が各値のパーセンタイル順位を算出している部分。
np.array(dfspl.rank(method='first', na_option='keep') - 1/2)/ rownum)
最初にDataFrameのrankを用いて各値の順位を求める。(参考: DatarFrameのrankのリファレンス)
その後、扱いやすいようndarrayに変換した後、データ数で割ってパーセンタイル順位をはじき出している。
-1/2しているのは、R言語のqqplot関数を用いるとこのような計算をしているから。
個人的には少し謎な部分で、-1/2しようがしまいが特に変わらないと思う。
上の式の外側の部分が以下。
stats.norm.ppf('上で記載した式', loc=0, scale=1)
ここでパーセンタイル順位がそれぞれ標準正規分布のどこに位置するかどうかの期待値を算出している。(参考: norm.ppfのリファレンス)
loc=0が平均の設定で、scale=1が分散の設定。
グラフをプロット
各種設定
色やグラフのサイズを設定する。
colorsets=['b','g','r']
xmin, xmax = -6, 6
ymin, ymax = 0, 100
xgrid, ygrid = 2, 10
散布図でプロット
for i in range(colnum):
dataname = dfspl.columns[i]
plt.scatter(norspl[:,i], npspl[:,i], color = colorsets[i], label = dataname)
plt.xlim([xmin, xmax])
plt.xticks(np.arange(xmin, xmax+1, xgrid))
plt.ylim([ymin, ymax])
plt.yticks(np.arange(ymin, ymax+1, ygrid))
plt.title('QQ-Plot')
plt.grid(linestyle='dashed')
plt.legend(loc=2)
plt.show()
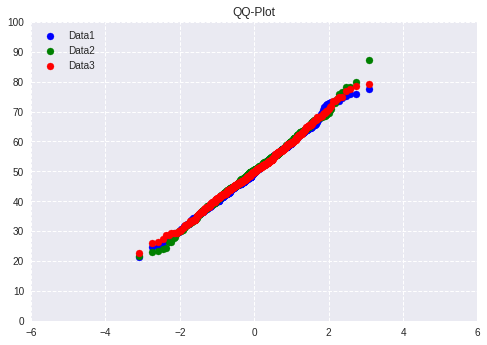
出力された確率プロット
以下のように線形になっていれば、正規分布に即したデータだと判断できる。