6DoF座標変換プログラムを作ってみたので,その考え方をメモしておく.
6DoFとは?
6DoF(6 Degrees of Freedom)とは,物体の位置と向きを表現する方法で,ロボット工学や航空工学でよく見かける概念だ.
空を飛んでいる鳥や飛行機やロケットなどを想像してみるのが分かりやすい.
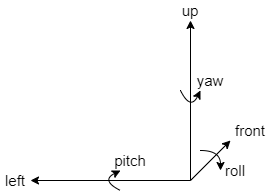
物体の位置を3つの数$(x,y,z)$で表現し,さらに物体の姿勢をロール,ピッチ,ヨーの3つの角度$(\phi,\theta,\psi)$で表現する.
$\phi$,$\theta$,$\psi$の単位はラジアンとする.
ここでは,位置$(x,y,z)$と姿勢$(\phi,\theta,\psi)$を合わせた概念を状態$(x,y,z,\phi,\theta,\psi)$と呼ぶ.
物体が状態$(x,y,z,\phi,\theta,\psi)$にあるとはどういうことか見てみよう.
- 状態$(0,0,0,0,0,0)$の物体を,$x$だけ前に進めた状態が$(x,0,0,0,0,0)$である.
- 状態$(x,0,0,0,0,0)$の物体を,$y$だけ左に進めた状態が$(x,y,0,0,0,0)$である.
- 状態$(x,y,0,0,0,0)$の物体を,$z$だけ上に進めた状態が$(x,y,z,0,0,0)$である.
ここで,物体の後ろから前に,右から左に,下から上に,それぞれ剣を刺してみよう.
- 状態$(x,y,z,0,0,0)$の物体を,後ろから前に刺した剣の柄を握って時計回りに角度$r$だけ回転させた状態が$(x,y,z,\phi,0,0)$である.
- 状態$(x,y,z,\phi,0,0)$の物体を,右から左に刺した剣の柄を握って時計回りに角度$p$だけ回転させた状態が$(x,y,z,\phi,\theta,0)$である.
- 状態$(x,y,z,\phi,\theta,0)$の物体を,下から上に刺した剣の柄を握って時計回りに角度$y$だけ回転させた状態が$(x,y,z,\phi,\theta,\psi)$である.
$\phi$,$\theta$,$\psi$の取り得る範囲は,$-\frac{\pi}{2}\le \phi<\frac{\pi}{2},-\pi\le \theta<\pi,0\le \psi<2\pi$とする.
3次元ベクトルクラス
状態を表現するための準備としてベクトルを実装する.
互いに直角な3つの単位ベクトル$\vec{e_x},\vec{e_y},\vec{e_z}$を基底ベクトルとする.
ここでは右手座標系を想定する.
つまり右手の親指,人差し指,中指を互いに直角になるように伸ばした時,親指が$\vec{e_x}$に,人差し指が$\vec{e_y}$に,中指が$\vec{e_z}$に,それぞれ対応する.
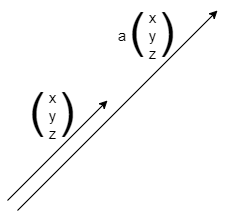
これら基底ベクトルの線形結合
\begin{pmatrix}
x\\
y\\
z\\
\end{pmatrix}
=x\vec{e_x}+y\vec{e_y}+z\vec{e_z}
を以下のクラスで表現する.
namespace Dynamics
{
class Vector
{
private:
double x, y, z;
public:
Vector(double x, double y, double z);
Vector(const Vector& vector);
~Vector();
double get_x()const;
double get_y()const;
double get_z()const;
Vector operator+()const;
Vector operator-()const;
Vector operator+(const Vector &vector)const;
Vector operator-(const Vector &vector)const;
Vector operator*(double a)const; // Scalar multiplication of vector
Vector operator/(double a)const; // Scalar division of vector
Vector operator*(const Vector &vector)const; // Cross product
double operator,(const Vector &vector)const; // Inner product
double operator/(const Vector &vector)const; // Angle between vectors
double operator/(const Dynamics::Plane& plane)const; // Angle between vector and plane
double operator!()const; // length
double operator*()const; // length ^ 2
Vector operator>>(const Plane& plane)const; // Projection of vector onto plane
// Vector rotation
// If the axis direction is forward and the angle is positive, rotate clockwise.
// If the axis direction is forward and the angle is negative, rotate counterclockwise.
Vector rotate(const Vector& axis, double angle/* radian */)const;
};
...
}
ベクトルの反転
-
\begin{pmatrix}
x\\
y\\
z\\
\end{pmatrix}
=
\begin{pmatrix}
-x\\
-y\\
-z\\
\end{pmatrix}
Dynamics::Vector Dynamics::Vector::operator-()const
{
return Dynamics::Vector(-this->x, -this->y, -this->z);
}
ベクトルの和
\begin{pmatrix}
x_1\\
y_1\\
z_1\\
\end{pmatrix}
+
\begin{pmatrix}
x_2\\
y_2\\
z_2\\
\end{pmatrix}
=
\begin{pmatrix}
x_1+x_2\\
y_1+y_2\\
z_1+z_2\\
\end{pmatrix}
Dynamics::Vector Dynamics::Vector::operator+(const Dynamics::Vector &vector)const
{
return Dynamics::Vector(x + vector.get_x(), y + vector.get_y(), z + vector.get_z());
}
ベクトルの差
\begin{pmatrix}
x_1\\
y_1\\
z_1\\
\end{pmatrix}
-
\begin{pmatrix}
x_2\\
y_2\\
z_2\\
\end{pmatrix}
=
\begin{pmatrix}
x_1-x_2\\
y_1-y_2\\
z_1-z_2\\
\end{pmatrix}
Dynamics::Vector Dynamics::Vector::operator-(const Dynamics::Vector &vector)const
{
return Dynamics::Vector(x - vector.get_x(), y - vector.get_y(), z - vector.get_z());
}
ベクトルのスカラー倍
a
\begin{pmatrix}
x\\
y\\
z\\
\end{pmatrix}
=
\begin{pmatrix}
ax\\
ay\\
az\\
\end{pmatrix}
Dynamics::Vector Dynamics::Vector::operator*(double a)const // Scalar multiplication of vector
{
return Dynamics::Vector(a * this->x, a * this->y, a * this->z);
}
Dynamics::Vector operator*(double a, const Dynamics::Vector& vector) // Scalar multiplication of vector
{
return vector * a;
}
ベクトルのスカラー分の一
\frac{\vec{v}}{a}=\frac{1}{a}\vec{v}
Dynamics::Vector Dynamics::Vector::operator/(double a)const // Scalar division of vector
{
return *this * (1 / a);
}
ベクトルの外積
\begin{pmatrix}
x_1\\
y_1\\
z_1\\
\end{pmatrix}
\times
\begin{pmatrix}
x_2\\
y_2\\
z_2\\
\end{pmatrix}
=
\begin{pmatrix}
y_1z_2-z_1y_2\\
z_1x_2-x_1z_2\\
x_1y_2-y_1x_2\\
\end{pmatrix}
Dynamics::Vector Dynamics::Vector::operator*(const Dynamics::Vector &vector)const // Cross product
{
return Dynamics::Vector(this->y * vector.get_z() - this->z * vector.get_y(), this->z * vector.get_x() - this->x * vector.get_z(), this->x * vector.get_y() - this->y * vector.get_x());
}
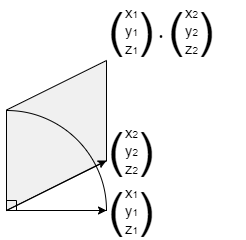
ベクトルの内積
\begin{pmatrix}
x_1\\
y_1\\
z_1\\
\end{pmatrix}
\cdot
\begin{pmatrix}
x_2\\
y_2\\
z_2\\
\end{pmatrix}
=x_1x_2+y_1y_2+z_1z_2
double Dynamics::Vector::operator,(const Dynamics::Vector &vector)const // Inner product
{
return this->x * vector.get_x() + this->y * vector.get_y() + this->z * vector.get_z();
}
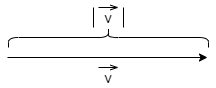
ベクトルの長さの2乗
|\vec{v}|^2=\vec{v}\cdot\vec{v}
double Dynamics::Vector::operator*()const // length ^ 2
{
return (*this, *this);
}
ベクトルの長さ
|\vec{v}|=\sqrt{\vec{v}\cdot\vec{v}}
double Dynamics::Vector::operator!()const // length
{
return std::sqrt(**this);
}
ベクトル同士のなす角
\angle\vec{v}\vec{w}=\frac{\vec{v}\cdot\vec{w}}{|\vec{v}||\vec{w}|}
double Dynamics::Vector::operator/(const Dynamics::Vector &vector)const // Angle between vectors
{
double denominator = !*this * !vector;
if(denominator == 0) // 少なくとも一方がゼロベクトルの場合角度を定義できない
{
ERROR();
return 0;
}
return std::acos((*this, vector) / denominator);
}
座標
ある点$P$の座標は,原点$O$からベクトル$\vec{v}$だけ進んだところ$P=O+\vec{v}$とみなせるので,座標もベクトルとして扱うことができる.
namespace Dynamics
{
...
using Coordinates = Vector;
...
}
平面クラス
状態を表現するための準備としてさらに平面を実装する.
点$P$と法線$\vec{n}$がある.
このとき,それぞれ$\vec{n}$に垂直で,互いに平行でない2つのベクトル$\vec{v},\vec{w}$を考え,平面
\{P+x\vec{v}+y\vec{w}|x\in\mathbb{R},y\in\mathbb{R}\}
を定義できる.
点$P$と法線$\vec{n}$で定義される平面を以下のクラスで表現する.
namespace Dynamics
{
...
class Plane
{
private:
Coordinates point; // The plane contains the point.
Vector normal; // The plane and the normal form a right angle.
public:
Plane(const Coordinates& point, const Vector& normal);
Plane(const Coordinates& a, const Coordinates& b, const Coordinates& c); // A plane containing given 3 points.
Plane(const Plane& plane);
~Plane();
Coordinates get_point()const;
Vector get_normal()const;
Coordinates operator-(const Coordinates& point)const; // Normal from point to plane
double operator/(const Plane &plane)const; // Angle between planes
double operator/(const Dynamics::Vector& vector)const; // Angle between plane and vector
};
...
}
相異なる3点を含む平面
相異なる3点$P,Q,R$を含む平面
\{P+x\vec{PQ}+y\vec{PR}|x\in\mathbb{R},y\in\mathbb{R}\}
は,点$P$を含み,$\vec{PQ}\times\vec{PR}$を法線とするから,
Dynamics::Plane::Plane(const Dynamics::Coordinates& a, const Dynamics::Coordinates& b, const Dynamics::Coordinates& c):Dynamics::Plane::Plane(a, (b - a) * (c - a)) // A plane containing given 3 points.
{
}
と書ける.
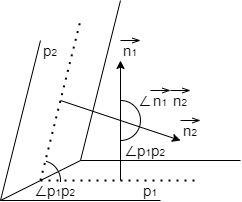
平面同士のなす角
$\vec{n_1}$,$\vec{n_2}$をそれぞれ法線とする平面$p_1$,$p_2$のなす角は,
\angle p_1p_2=\pi-\angle\vec{n_1}\vec{n_2}
なので,
double Dynamics::Plane::operator/(const Plane &plane)const // Angle between planes
{
return M_PI - (this->normal / plane.normal);
}
ベクトルと平面のなす角
ベクトル$\vec{v}$と法線$\vec{n}$とする平面$p$とのなす角は,
\angle\vec{v}p=\frac{\pi}{2}-\angle\vec{v}\vec{n}
なので,
double Dynamics::Vector::operator/(const Dynamics::Plane& plane)const // Angle between vector and plane
{
return std::abs(M_PI / 2 - (*this / plane.get_normal()));
}
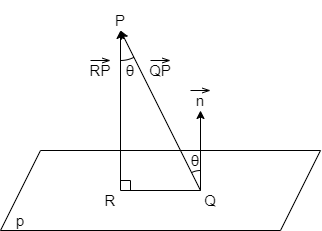
平面から点への法線
点$P$と,点$Q$を含みベクトル$\vec{n}$を法線とする平面$p$がある.
また,点$P$から平面$p$への垂線と平面$p$との交点$R$があり,$\angle QPR$の大きさを$\theta$とする.
平面$p$から点$P$への法線$P-p$は
\begin{align}
P-p&=\vec{RP}\\
&=|\vec{RP}|\frac{\vec{n}}{|\vec{n}|}\\
&=|\vec{QP}|\cos\theta\frac{\vec{n}}{|\vec{n}|}\\
&=|\vec{QP}|\frac{\vec{QP}\cdot\vec{n}}{|\vec{QP}||\vec{n}|}\frac{\vec{n}}{|\vec{n}|}\\
&=\frac{\vec{QP}\cdot\vec{n}}{\vec{n}\cdot\vec{n}}\vec{n}
\end{align}
なので,
Dynamics::Coordinates operator-(const Dynamics::Coordinates& point, const Dynamics::Plane& plane) // Normal from plane to point
{
Dynamics::Vector n = plane.get_normal();
Dynamics::Vector qp = point - plane.get_point();
return ((qp , n) / *n) * n;
}
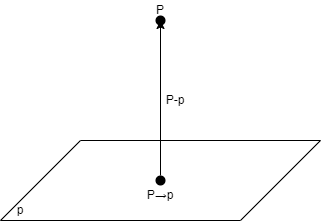
点の平面への投影
点$P$の平面$p$への投影$P\rightarrow p$は,
\begin{align}
P\rightarrow p+(P-p)&=P\\
P\rightarrow p&=P-(P-p)
\end{align}
なので,
Dynamics::Coordinates operator>(const Dynamics::Coordinates& point, const Dynamics::Plane& plane) // Projection of point onto plane
{
return point - (point - plane);
}
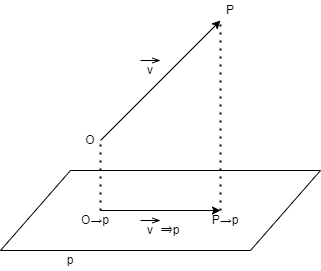
ベクトルの平面への投影
原点$O$から点$P$へのベクトル$\vec{v}$の平面$p$への投影$\vec{v}\Rightarrow p$は,
\begin{align}
\vec{v}\Rightarrow p&=\vec{OP}\Rightarrow p\\
&=(P\rightarrow p)-(O\rightarrow p)\\
&=(\vec{v}\rightarrow p)-(O\rightarrow p)
\end{align}
なので,
Dynamics::Vector Dynamics::Vector::operator>>(const Dynamics::Plane& plane)const // Projection of vector onto plane
{
return (*this > plane) - (Dynamics::Vector(0, 0, 0) > plane);
}
姿勢と回転
姿勢を実装する準備としてベクトルと平面を実装したところで,いよいよ姿勢を実装していく.
前述したとおり姿勢はロール,ピッチ,ヨーの3つの回転の組み合わせとして表される.
この姿勢の表現方法は合理的ではあるが,抽象的でとっつきにくくもある.
ロール,ピッチ,ヨーの値を見てその姿勢をぱっと想像できる人はそういないだろう.
姿勢を表すもう一つの方法として,3つのベクトルを用いるものがある.
状態の説明で物体に3本の剣を刺す例えで説明したが,その剣がベクトルなのだ.
実はベクトルは2本あれば姿勢を決定するのに十分なのだが,時間計算量と空間計算量のバランスや,プログラムの美しさを考えると3本がいいように思うので3本とした.
物体に刺さった3本の剣は互いに直角で,1本の剣の柄を握って回すと,その剣を回転軸として他の2本の剣が向きを変える.
これは1本のベクトルを回転軸とし,他の2本のベクトルが回転することを意味する.
ベクトルの回転
ベクトル$\vec{u}$を,ベクトル$\vec{a}$を回転軸として,$\vec{a}$の始点が後ろに,$\vec{a}$の終点が前となるような視点において,時計回りに角度$\theta$だけ回転させたベクトル$\vec{z}$を求めたい.
ベクトル$\vec{a}$を法線とする平面を$p$とすると,
\begin{align}
\vec{v}&=\vec{u}\Rightarrow p\\
\vec{w}&=\vec{u}-\vec{v}\\
\vec{x}&=\frac{\vec{a}\times\vec{v}}{|\vec{a}|}\\
\vec{y}&=\vec{v}\cos\theta+\vec{x}\sin\theta\\
\vec{z}&=\vec{w}+\vec{y}
\end{align}
なので,
// Vector rotation
// If the axis direction is forward and the angle is positive, rotate clockwise.
// If the axis direction is forward and the angle is negative, rotate counterclockwise.
Dynamics::Vector Dynamics::Vector::rotate(const Dynamics::Vector& axis, double angle/* radian */)const
{
if(*axis == 0) // 回転軸がゼロベクトルの場合,回転を定義できない.
{
ERROR();
return Dynamics::Vector(0, 0, 0);
}
if(**this == 0)return *this; // ゼロベクトルは回転しても変化しない.
if(*this / axis == 0)return *this; // 回転軸が自身と平行な場合,回転しても変化しない.
Dynamics::Plane p(Dynamics::Vector(0, 0, 0), axis);
Dynamics::Vector v = *this >> p;
Dynamics::Vector w = *this - v;
Dynamics::Vector x = axis * v / !axis;
Dynamics::Vector y = std::cos(angle) * v + std::sin(angle) * x;
return w + y;
}
ロドリゲスの回転行列というものがあり,それとベクトルを掛け合わせるというのがこれと全く同じことをしているのだが,この回転行列は記憶力のない私には到底暗記できそうにない3次正方行列で中身を理解できないブラックボックスなので,ロドリゲスの回転行列の意味を理解するためにこのような実装とした.
姿勢クラス
姿勢クラスは,ロール,ピッチ,ヨーの角度による表現と,3本のベクトルによる表現を両方持ち,コンストラクタもそれぞれの表現に対応したものを持つ.
3本のベクトルはそれぞれ以下のとおりである.
- frontは物体の後ろから前に刺した剣で,前方向ベクトルと呼ぶ.
- leftは物体の右から左に刺した剣で,左方向ベクトルと呼ぶ.
- upは物体の下から上に刺した剣で,上方向ベクトルと呼ぶ.
set_front_upはベクトルによる姿勢表現を角度による姿勢表現に変換するメソッドで,コンストラクタのみから呼び出されるプライベートメソッドである.
また,前述のとおり姿勢は2本のベクトルで決定するため,このメソッドは前方向ベクトルと上方向ベクトルのみを引数としている.
namespace Dynamics
{
...
class Posture
{
private:
// ロール,ピッチ,ヨーの各回転角度
double roll, pitch, yaw; // radian
// -M_PI / 2 <= roll < M_PI / 2
// -M_PI <= pitch < M_PI
// 0 <= yaw < 2 * M_PI
Vector front, left, up; // 姿勢を表す3本のベクトル
void set_front_up(const Vector& front, const Vector& up);
public:
Posture(double roll, double pitch, double yaw);
Posture(const Vector& front, const Vector& up);
Posture(const Posture& posture);
~Posture();
double get_roll()const;
double get_pitch()const;
double get_yaw()const;
Vector get_front()const;
Vector get_back()const;
Vector get_left()const;
Vector get_right()const;
Vector get_up()const;
Vector get_down()const;
Posture operator+()const; // Identity map
Posture operator-()const; // Reverse rotation
Posture operator+(const Posture& posture)const; // Synthesize rotations
Posture operator-(const Posture& posture)const; // Synthesize reverse rotation
Vector operator*(const Vector& vector)const; // Apply rotation to vector
};
...
}
ベクトルの表現方法から角度による表現方法への変換
まず,与えられた前方向ベクトルと上方向ベクトルが正しいかどうかを確認している.
これらのベクトルはゼロベクトルであってはならず,互いに直角でなければならない.
直角条件についてはどうしても誤差が発生するため,$\pm1$度の誤差を許容している.
次に方向ベクトルの設定を行っている.
前方向ベクトルと上方向ベクトルは単位ベクトル化して設定し,左方向ベクトルは上方向ベクトルと前方向ベクトルの外積として求まる.
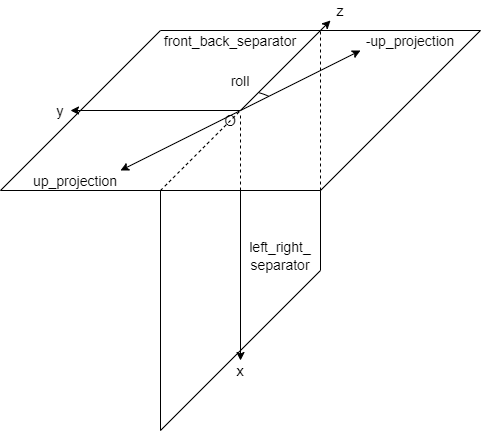
次に4つの点$O=(0,0,0),X=(1,0,0),Y=(0,1,0),Z=(0,0,1)$を用意し,それらを用いてyz平面front_back_separatorとxz平面left_right_separatorを用意する.
上方向ベクトルのyz平面への投影をup_projectionとする.
ロール角の算出
ロール角はベクトル$\vec{OZ}$とup_projectionのなす角である.
up_projectionが右上を向いている時,ロール角は正である.
up_projectionが左上を向いている時,ロール角は負である.
up_projectionが左下を向いている時は,ベクトル$\vec{OZ}$とup_projectionのなす角は$\frac{\pi}{2}$を超えるが,ロール角の範囲は$-\frac{\pi}{2}\le r<-\frac{\pi}{2}$のため範囲外である.
この場合は,ベクトル$\vec{OZ}$と-up_projectionのなす角をロール角とすればよい.
-up_projectionは右上を向いているため,ロール角は正となる.
up_projectionを反転させてしまっているが,ロール回転の後のピッチ回転でもう一度反転することによりup_projectionの方向を元に戻すことができる.
up_projectionが右下を向いている時も同様にベクトル$\vec{OZ}$と-up_projectionのなす角をロール角とする.
このとき-up_projectionは左上を向いているため,ロール角は負となる.
これらをまとめると,ロール角の絶対値は平面left_right_separatorとup_projectionのなす角であり,ロール角の符号はup_projectionのy成分とz成分の符号が異なる場合は正,同じ場合は負であるということになる.
up_projectionがゼロベクトルの場合,これはピッチ角が$\pm\frac{\pi}{2}$でロール回転軸とヨー回転軸が共に$x$軸と平行する.
これはロール回転とヨー回転の融合を意味し,計算上はup_projectionと平面left_right_separatorとのなす角が定義できなくなるという現象として現れる.
この場合,ロール角は0としてよい.
ピッチ角の算出
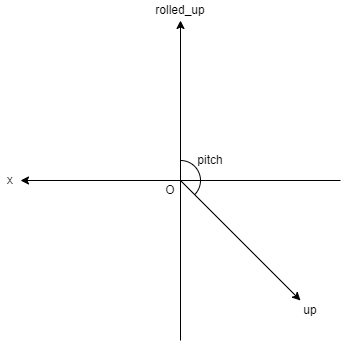
ベクトル$\vec{OZ}$に,ロール回転をかけたベクトルrolled_upを作る.
ピッチ角は,rolled_upと上方向ベクトルのなす角である.
上方向ベクトルが前方上方を向いている時,ピッチ角は正である.
上方向ベクトルが前方下方を向いている時,ピッチ角は正である.
上方向ベクトルが後方上方を向いている時,ピッチ角は負である.
上方向ベクトルが後方下方を向いている時,ピッチ角は負である.
これらをまとめると,ピッチ角の符号は,rolled_upと上方向ベクトルのなす角である.
ピッチ角の符号は,上方向ベクトルのx成分の符号と同じである.
ヨー角の算出
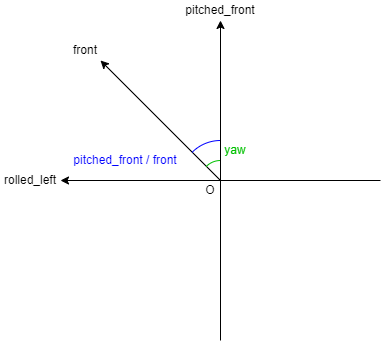
$\vec{OY}$にロール回転をかけてベクトルrolled_leftとし,$\vec{OX}$にピッチ回転をかけてベクトルpitched_frontとする.
前方向ベクトルが左前を向いているとき,ヨー角はpitched_frontと前方向ベクトルのなす角である.
前方向ベクトルが左後ろを向いている時も,ヨー角はpitched_frontと前方向ベクトルのなす角である.
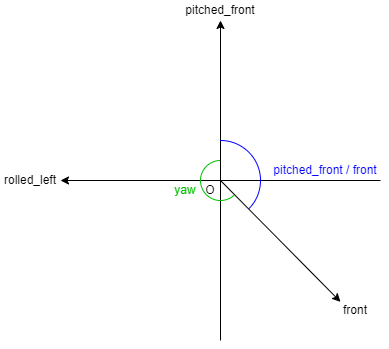
前方向ベクトルが右前を向いている時とき,ヨー角はpitched_frontと前方向ベクトルのなす角の反対側の角である.
前方向ベクトルが右後ろを向いているときも,ヨー角はpitched_frontと前方向ベクトルのなす角の反対側の角である.
これらをまとめると,rolled_leftと前方向ベクトルのなす角が$\frac{\pi}{2}$以下の場合,ヨー角はpitched_frontと前方向ベクトルのなす角である.
一方,rolled_leftと前方向ベクトルのなす角が$\frac{\pi}{2}$より大きい場合,ヨーはpitched_frontと前方向ベクトルのなす角の反対側の角である.
変換プログラム
以上をプログラムに書き起こすと以下のようになる.
void Dynamics::Posture::set_front_up(const Vector& front, const Vector& up)
{
// 前方向ベクトルはゼロベクトルであってはならない.
if(*front == 0)
{
ERROR();
return;
}
// 上方向ベクトルはゼロベクトルであってはならない.
if(*up == 0)
{
ERROR();
return;
}
// 前方向ベクトルと上方向ベクトルは直角でなければならない.
if(Dynamics::angle_error_limit <= std::abs(M_PI / 2 - (front / up)))
{
ERROR();
return;
}
this->front = front / !front; // 前方向ベクトルの単位ベクトル化
this->up = up / !up; // 上方向ベクトルの単位ベクトル化
this->left = up * front; // 左方向ベクトル
// Adjust roll
Dynamics::Coordinates o(0, 0, 0);
Dynamics::Coordinates x(1, 0, 0);
Dynamics::Coordinates y(0, 1, 0);
Dynamics::Coordinates z(0, 0, 1);
Dynamics::Plane front_back_separator(o, y, z);
Dynamics::Plane left_right_separator(x, o, z);
Dynamics::Vector up_projection = this->up >> front_back_separator;
if(up_projection.get_y() == 0)this->roll = 0;
else if(up_projection.get_y() * up_projection.get_z() < 0)this->roll = up_projection / left_right_separator;
else this->roll = -(up_projection / left_right_separator);
// Adjust pitch
Dynamics::Vector rolled_up = z.rotate(x, this->roll);
if(0 < this->up.get_x())this->pitch = rolled_up / this->up;
else this->pitch = -(rolled_up / this->up);
// Adjust yaw
Dynamics::Vector rolled_left = y.rotate(x, this->roll);
Dynamics::Vector pitched_front = x.rotate(rolled_left, this->pitch);
if(rolled_left / this->front <= M_PI / 2)this->yaw = pitched_front / this->front;
else this->yaw = 2 * M_PI - (pitched_front / this->front);
}
ロール,ピッチ,ヨーによるコンストラクタ
はじめにロール,ピッチ,ヨー全て0であるときの前方向ベクトル,左方向ベクトル,上方向ベクトルを用意する.
このとき,前方向ベクトル,左方向ベクトル,上方向ベクトルはそれぞれ$\vec{e_x}$,$\vec{e_y}$,$\vec{e_z}$に等しい.
その後,この3本のベクトルに対し,ロール回転,ピッチ回転,ヨー回転を順番に適用していく.
ベクトルの回転はロドリゲス回転行列の掛け算であり,交換法則は成り立たないためロール,ピッチ,ヨーの回転順序を入れ替えることはできないことに注意しよう.
最後にset_front_upメソッドを実行し,前方向ベクトルと上方向ベクトルから,左方向ベクトル,ロール,ピッチ,ヨーの設定を行う.
こうすることで,コンストラクタに与えられたロール,ピッチ,ヨーが範囲外であっても,同じ姿勢を表す範囲内の数値に修正することができる.
Dynamics::Posture::Posture(double roll, double pitch, double yaw): roll(0), pitch(0), yaw(0), front(0, 0, 0), left(0, 0, 0), up(0, 0, 0)
{
Dynamics::Coordinates front(1, 0, 0);
Dynamics::Coordinates left(0, 1, 0);
Dynamics::Coordinates up(0, 0, 1);
// Roll rotation
front = front.rotate(front, roll);
left = left.rotate(front, roll);
up = up.rotate(front, roll);
// Pitch rotation
front = front.rotate(left, pitch);
left = left.rotate(left, pitch);
up = up.rotate(left, pitch);
// Yaw rotation
front = front.rotate(up, yaw);
left = left.rotate(up, yaw);
up = up.rotate(up, yaw);
this->set_front_up(front, up);
}
ベクトルによるコンストラクタ
ベクトルによる姿勢の初期化では,前方向ベクトルと上方向ベクトルを引数にとり,set_front_upメソッドにより左方向ベクトル,ロール,ピッチ,ヨー角を設定する.
Dynamics::Posture::Posture(const Vector& front, const Vector& up): roll(0), pitch(0), yaw(0), front(0, 0, 0), left(0, 0, 0), up(0, 0, 0)
{
set_front_up(front, up);
}
逆姿勢
ロール角$\phi$,ピッチ角$\theta$,ヨー角$\psi$である姿勢$(\phi,\theta,\psi)$は,基準姿勢$(0,0,0)$から見た姿勢を表している.
逆に姿勢$(\phi,\theta,\psi)$からみた基準姿勢$(0,0,0)$がどのように見えるかを表すのが逆姿勢である.
逆姿勢は,姿勢を表す回転行列の逆行列ということもできる.
ロール回転行列を$\Phi$,ピッチ回転行列を$\Theta$,ヨー回転行列を$\Psi$とすると,姿勢を表す回転行列は$\Phi\Theta\Psi$となる.
これに,ヨー回転の逆行列$\Psi^{-1}$,ピッチ回転の逆行列$\Theta^{-1}$,ロール回転の逆行列$\Phi^{-1}$を順番にかけると,$\Phi\Theta\Psi\Psi^{-1}\Theta^{-1}\Phi^{-1}=E$となる.
これは姿勢$\Phi\Theta\Psi$から見た姿勢$\Phi\Theta\Psi$を意味する.
単位行列は基準姿勢を意味し,姿勢を表す回転行列にその逆行列を掛けることで基準姿勢に戻ることがわかる.
この逆行列$\Psi^{-1}\Theta^{-1}\Phi^{-1}$を,基準姿勢つまり単位行列にかけると,これは姿勢$\Phi\Theta\Psi$から見た基準姿勢$E$を意味する.
つまり逆姿勢である.
プログラムでは,thisの前方向ベクトルthis_front,左方向ベクトルthis_left,上方向ベクトルthis_up,基準姿勢の前方向ベクトルreverse_front,左方向ベクトルreverse_left,上方向ベクトルreverse_upの計6本のベクトルを用意する.
これら6本のベクトルに,逆向きのヨー回転,逆向きのピッチ回転,逆向きのロール回転を順番に適用することで,前方向ベクトルreverse_front,左方向ベクトルreverse_left,上方向ベクトルreverse_upはもとの姿勢の逆姿勢になる.
最後に前方向ベクトルreverse_frontと上方向ベクトルreverse_upから逆姿勢を生成して返している.
Dynamics::Posture Dynamics::Posture::operator-()const // Reverse rotation
{
// 自身の姿勢を表すベクトル
Dynamics::Vector this_front(this->front);
Dynamics::Vector this_left(this->left);
Dynamics::Vector this_up(this->up);
// 基準姿勢を表すベクトル
Dynamics::Vector reverse_front(1, 0, 0);
Dynamics::Vector reverse_left(0, 1, 0);
Dynamics::Vector reverse_up(0, 0, 1);
// 逆向きのヨー回転を掛ける
this_front = this_front.rotate(this_up, -this->yaw);
this_left = this_left.rotate(this_up, -this->yaw);
this_up = this_up.rotate(this_up, -this->yaw);
reverse_front = reverse_front.rotate(this_up, -this->yaw);
reverse_left = reverse_left.rotate(this_up, -this->yaw);
reverse_up = reverse_up.rotate(this_up, -this->yaw);
// 逆向きのピッチ回転を掛ける
this_front = this_front.rotate(this_left, -this->pitch);
this_left = this_left.rotate(this_left, -this->pitch);
this_up = this_up.rotate(this_left, -this->pitch);
reverse_front = reverse_front.rotate(this_left, -this->pitch);
reverse_left = reverse_left.rotate(this_left, -this->pitch);
reverse_up = reverse_up.rotate(this_left, -this->pitch);
// 逆向きのロール回転を掛ける
this_front = this_front.rotate(this_front, -this->roll);
this_left = this_left.rotate(this_front, -this->roll);
this_up = this_up.rotate(this_front, -this->roll);
reverse_front = reverse_front.rotate(this_front, -this->roll);
reverse_left = reverse_left.rotate(this_front, -this->roll);
reverse_up = reverse_up.rotate(this_front, -this->roll);
// 逆回転を掛けた前方向ベクトルと上方向ベクトルから逆姿勢を作成する.
return Dynamics::Posture(reverse_front, reverse_up);
}
合成姿勢
合成姿勢は,自身の姿勢に,相手の姿勢を表す回転行列を掛けることで行う.
プログラムでは,thisの前方向ベクトルsynthetic_front,左方向ベクトルsynthetic_left,上方向ベクトルsynthetic_up,基準姿勢の前方向ベクトルbase_front,左方向ベクトルbase_left,上方向ベクトルbase_upの計6本のベクトルを用意する.
基準姿勢のベクトルに相手の姿勢のロール回転,ピッチ回転,ヨー回転を順に掛けて基準姿勢を相手の姿勢に変えていくのと同時に,自身の姿勢のベクトルにも同じ回転を掛けることで,合成姿勢のベクトルを作っている.
最後に,前方向ベクトルsynthetic_frontと上方向ベクトルsynthetic_upから合成姿勢を作成して返している.
Dynamics::Posture Dynamics::Posture::operator+(const Dynamics::Posture& posture)const // Synthesize rotations
{
// 基準姿勢のベクトル
Dynamics::Vector base_front(1, 0, 0);
Dynamics::Vector base_left(0, 1, 0);
Dynamics::Vector base_up(0, 0, 1);
// 自身の姿勢のベクトル
Dynamics::Vector synthetic_front(this->front);
Dynamics::Vector synthetic_left(this->left);
Dynamics::Vector synthetic_up(this->up);
// 相手のロール回転を掛ける
base_front = base_front.rotate(base_front, posture.roll);
base_left = base_left.rotate(base_front, posture.roll);
base_up = base_up.rotate(base_front, posture.roll);
synthetic_front = synthetic_front.rotate(base_front, posture.roll);
synthetic_left = synthetic_left.rotate(base_front, posture.roll);
synthetic_up = synthetic_up.rotate(base_front, posture.roll);
// 相手のピッチ回転を掛ける
base_front = base_front.rotate(base_left, posture.pitch);
base_left = base_left.rotate(base_left, posture.pitch);
base_up = base_up.rotate(base_left, posture.pitch);
synthetic_front = synthetic_front.rotate(base_left, posture.pitch);
synthetic_left = synthetic_left.rotate(base_left, posture.pitch);
synthetic_up = synthetic_up.rotate(base_left, posture.pitch);
// 相手のヨー回転を掛ける
base_front = base_front.rotate(base_up, posture.yaw);
base_left = base_left.rotate(base_up, posture.yaw);
base_up = base_up.rotate(base_up, posture.yaw);
synthetic_front = synthetic_front.rotate(base_up, posture.yaw);
synthetic_left = synthetic_left.rotate(base_up, posture.yaw);
synthetic_up = synthetic_up.rotate(base_up, posture.yaw);
// 回転を合成した前方向ベクトルと上方向ベクトルから合成姿勢を作成する.
return Dynamics::Posture(synthetic_front, synthetic_up);
}
逆姿勢の合成
Dynamics::Posture Dynamics::Posture::operator-(const Dynamics::Posture& posture)const // Synthesize reverse rotation
{
return *this + -posture;
}
ベクトルへの回転の適用
基準姿勢のベクトルを用意し,これにロール回転,ピッチ回転,ヨー回転を掛けていくのと同時に回転対象のベクトルにも同じ回転を掛けることで,自身の姿勢と同じ回転のかかったベクトルを作成する.
Dynamics::Vector Dynamics::Posture::operator*(const Dynamics::Vector& vector)const // Apply rotation to vector
{
// 基準姿勢のベクトル
Dynamics::Vector base_front(1, 0, 0);
Dynamics::Vector base_left(0, 1, 0);
Dynamics::Vector base_up(0, 0, 1);
Dynamics::Vector rotated_vector = vector;
// ロール回転を掛ける
base_front = base_front.rotate(base_front, this->roll);
base_left = base_left.rotate(base_front, this->roll);
base_up = base_up.rotate(base_front, this->roll);
rotated_vector = rotated_vector.rotate(base_front, this->roll);
// ピッチ回転を掛ける
base_front = base_front.rotate(base_left, this->pitch);
base_left = base_left.rotate(base_left, this->pitch);
base_up = base_up.rotate(base_left, this->pitch);
rotated_vector = rotated_vector.rotate(base_left, this->pitch);
// ヨー回転を掛ける
base_front = base_front.rotate(base_up, this->yaw);
base_left = base_left.rotate(base_up, this->yaw);
base_up = base_up.rotate(base_up, this->yaw);
rotated_vector = rotated_vector.rotate(base_up, this->yaw);
// 回転を掛けたベクトルを返す
return rotated_vector;
}
状態クラス
座標クラスと姿勢クラスを組み合わせることで,状態クラスを作る
コンストラクタは座標と姿勢を指定するものと,座標のx成分,y成分,z成分,姿勢のロール角,ピッチ角,ヨー角を個別に指定するものとがある.
姿勢クラスと同じように逆状態,合成状態,逆状態の合成があり,さらに相対状態から絶対状態への変換,絶対状態から相対状態への返還などを実装している.
namespace Dynamics
{
...
class State
{
private:
Coordinates coordinates; // 座標
Posture posture; // 姿勢
public:
State(const Coordinates& coordinates, const Posture& posture);
State(double x, double y, double z, double roll, double pitch, double yaw);
State(const State& state);
~State();
Coordinates get_coordinates()const;
Posture get_posture()const;
State operator+()const; // Identity map
State operator-()const; // Reverse state
State operator+(const State& state)const; // Synthesize states
State operator-(const State& state)const; // Synthesize reverse states
State to_absolute(const State& viewpoint)const;
State to_relative(const State& viewpoint)const;
};
...
}
コンストラクタ
前述のとおり,座標と姿勢を指定するものと,座標のx成分,y成分,z成分,姿勢のロール角,ピッチ角,ヨー角を個別に指定するものとがある.
Dynamics::State::State(const Dynamics::Coordinates& coordinates, const Dynamics::Posture& posture):coordinates(coordinates), posture(posture)
{
}
Dynamics::State::State(double x, double y, double z, double roll, double pitch, double yaw):coordinates(x, y, z), posture(roll, pitch, yaw)
{
}
逆状態
自身の状態が$(x,y,z,\phi,\theta,\psi)$のとき,その状態から見た基準状態$(0,0,0,0,0,0)$はどのように見えるだろうか?
姿勢に関しては単純に$(\phi,\theta,\psi)$の逆姿勢となる.
位置に関しては$(x,y,z)$を反転した$(-x,-y,-z)$を,$(\phi,\theta,\psi)$の逆姿勢からみたベクトルとなるため,$(-x,-y,-z)$に逆姿勢の回転を掛けたものとなる.
Dynamics::State Dynamics::State::operator-()const // Reverse state
{
return Dynamics::State((-this->posture) * (-this->coordinates), -this->posture);
}
合成状態
自身の状態に別の状態を合成すると,姿勢は単純に合成され,位置は自身の位置に,相手の位置に自身の姿勢の回転を作用させたベクトルを足したものとなる.
Dynamics::State Dynamics::State::operator+(const Dynamics::State& state)const // Synthesize states
{
return Dynamics::State(this->coordinates + (this->posture * state.coordinates), state.posture + this->posture);
}
逆状態の合成
Dynamics::State Dynamics::State::operator-(const Dynamics::State& state)const // Synthesize reverse states
{
return *this + -state;
}
相対状態から絶対状態への変換
ここまで来れば6DoF座標変換はほぼできたも同然である.
状態クラスにおいて*thisがある状態viewpointから見た相対状態であるとき,その相対状態を基準状態$(0,0,0,0,0,0)$から見た絶対状態はどうなるだろうか?
これは,視点viewpointと相対状態*thisの合成で実現できる.
状態の合成に交換法則は成り立たないので順番を入れ替えてはいけないことに注意が必要である.
Dynamics::State Dynamics::State::to_absolute(const State& viewpoint)const
{
return viewpoint + *this;
}
絶対状態から相対状態への変換
逆に,*thisが絶対状態であるとき,その絶対状態を視点viewpointから見るとどのように見えるだろうか?
これは絶対状態*thisを視点viewpointから見た相対状態であり,視点viewpointの逆状態に,絶対状態*thisを合成すればよい.
Dynamics::State Dynamics::State::to_relative(const State& viewpoint)const
{
return -viewpoint + *this;
}