はじめに
こんにちは.たいみょーじんです.
この記事は,自作OS Advent Calendar 2022の11日目の記事です.
昨日の記事でFPUを用いた実数の演算ができるようになったので,今回はFPUによる実数演算を応用して複素数演算をやってみましょう.
この記事を通して,実数演算から複素数演算が構築されていく様子が体験できればと思います.
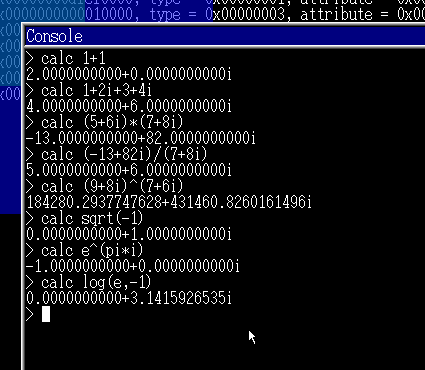
複素数計算アプリ
haribote OSベースのの自作OS hariboslinuxには,こんな感じの複素数計算アプリが入っています.
(複素数計算アプリのソースコード)
複素数の実装
では,ソースコードを見ながら,複素数の実装を見ていきましょう.
まず複素数を表す構造体を定義します.
typedef struct
{
double real;
double imag;
} Complex;
以下,各種複素数の演算の実装を見ていきます.
足し算
(a+bi)+(c+di)=(a+c)+(b+d)i
なので,
Complex complex_addition(Complex a, Complex b)
{
Complex result;
result.real = a.real + b.real;
result.imag = a.imag + b.imag;
return result;
}
引き算
(a+bi)-(c+di)=(a-c)+(b-d)i
なので,
Complex complex_subtraction(Complex a, Complex b)
{
Complex result;
result.real = a.real - b.real;
result.imag = a.imag - b.imag;
return result;
}
掛け算
\begin{align}
(a+bi)(c+di)&=ac+adi+bic+bidi\\
&=ac+adi+bci+bdi^2\\
&=ac+adi+bci-bd\\
&=(ac-bd)+(ad+bc)i
\end{align}
なので,
Complex complex_multiplication(Complex a, Complex b)
{
Complex result;
result.real = a.real * b.real - a.imag * b.imag;
result.imag = a.real * b.imag + a.imag * b.real;
return result;
}
割り算
\frac{a+bi}{c+di}=e+fi
とすると,
\begin{align}
a+bi&=(c+di)(e+fi)\\
&=(ce-df)+(cf+de)i
\end{align}
なので
\left\{
\begin{align}
a&=ce-df\\
b&=de+cf
\end{align}
\right.
を$e$と$f$について解くと,
\left\{
\begin{align}
e&=\frac{ac+bd}{c^2+d^2}\\
b&=\frac{bc-ad}{c^2+d^2}\\
\end{align}
\right.
よって
\frac{a+bi}{c+di}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i
なので,
Complex complex_division(Complex a, Complex b)
{
Complex result;
result.real = (a.real * b.real + a.imag * b.imag) / (b.real * b.real + b.imag * b.imag);
result.imag = (a.imag * b.real - a.real * b.imag) / (b.real * b.real + b.imag * b.imag);
return result;
}
絶対値
|a+bi|=\sqrt{a^2+b^2}
なので,
Complex complex_abs(Complex a)
{
Complex result;
result.real = sqrt(a.real * a.real + a.imag * a.imag);
result.imag = 0.0;
return result;
}
指数関数
\begin{align}
e^{a+bi}&=e^ae^{bi}\\
&=e^a(\cos{b}+i\sin{b})\\
&=e^a\cos{b}+ie^a\sin{b}
\end{align}
なので,
Complex complex_exp(Complex exponent)
{
Complex result;
result.real = exp(exponent.real) * cos(exponent.imag);
result.imag = exp(exponent.real) * sin(exponent.imag);
return result;
}
対数関数
複素数$z$に対して,
\log{z}=a+bi
とすると,
\begin{align}
z&=e^{a+bi}\\
&=e^ae^{bi}\\
&=e^a(\cos{b}+i\sin{b})
\end{align}
ここで,$z$の絶対値は
\begin{align}
|z|&=|e^a(\cos{b}+i\sin{b})|\\
&=e^a|\cos{b}+i\sin{b}|\\
&=e^a\sqrt{\cos^2b+\sin^2b}\\
&=e^a
\end{align}
$z$の偏角は,
\begin{align}
\arg{z}&=\arg(e^a(\cos{b}+i\sin{b}))\\
&=\arg(\cos{b}+i\sin{b})\\
&=\tan^{-1}(\cos{b},\sin{b})\\
&=b
\end{align}
よって,
\begin{align}
\log{z}&=a+bi\\
&=\log|z|+i\arg{z}
\end{align}
なので,
Complex complex_log(Complex power)
{
Complex result;
result.real = log(complex_abs(power).real);
result.imag = atan2(power.imag, power.real);
return result;
}
冪乗
指数関数と対数関数を実装すると,任意の複素数$x,y$の冪乗$x^y$を以下のように実装できます.
\begin{align}
x^y&=(e^{\log{x}})^y\\
&=e^{y\log{x}}
\end{align}
なので,
Complex complex_pow(Complex base, Complex exponent)
{
return complex_exp(complex_multiplication(exponent, complex_log(base)));
}
三角関数
複素数の三角関数はオイラーの公式
e^{i\theta}=\cos\theta+i\sin\theta
の$\theta$を実数から複素数に拡張することで定義されます.
任意の複素数$z$をオイラーの公式に代入して,
e^{iz}=\cos{z}+i\sin{z}
また$-z$をオイラーの公式に代入して,$\cos$と$\sin$は複素数に拡張しても偶関数,奇関数の性質を保つとすると,
\begin{align}
e^{-iz}&=\cos(-z)+i\sin(-z)\\
&=\cos{z}-i\sin{z}
\end{align}
上の2つの式を引き算すると,
\begin{align}
e^{iz}-e^{-iz}&=\cos{z}+i\sin{z}-(\cos{z}-i\sin{z})\\
&=2i\sin{z}
\end{align}
よって,
\sin{z}=\frac{e^{iz}-e^{-iz}}{2i}
逆に足し算すると$\cos$が定義されます.
\begin{align}
e^{iz}+e^{-iz}&=\cos{z}+i\sin{z}+(\cos{z}-i\sin{z})\\
&=2\cos{z}
\end{align}
よって,
\cos{z}=\frac{e^{iz}+e^{-iz}}{2}
さらに$\tan\theta=\frac{\sin\theta}{\cos\theta}$が複素数でも成り立つとすると,$\tan$も実装できます.
これをプログラムにすると,
Complex complex_sin(Complex theta)
{
Complex i;
Complex minus_i;
Complex two_i;
i.real = 0.0;
i.imag = 1.0;
minus_i.real = 0.0;
minus_i.imag = -1.0;
two_i.real = 0.0;
two_i.imag = 2.0;
return complex_division(complex_subtraction(complex_exp(complex_multiplication(theta, i)), complex_exp(complex_multiplication(theta, minus_i))), two_i);
}
Complex complex_cos(Complex theta)
{
Complex i;
Complex minus_i;
Complex two;
i.real = 0.0;
i.imag = 1.0;
minus_i.real = 0.0;
minus_i.imag = -1.0;
two.real = 2.0;
two.imag = 0.0;
return complex_division(complex_addition(complex_exp(complex_multiplication(theta, i)), complex_exp(complex_multiplication(theta, minus_i))), two);
}
Complex complex_tan(Complex theta)
{
return complex_division(complex_sin(theta), complex_cos(theta));
}
逆三角関数
複素数の三角関数を定義すると,そこから複素数の逆三角関数が求まります.
$y=\sin{x}$とすると,
\begin{align}
y&=\sin{x}\\
&=\frac{e^{ix}-e^{-ix}}{2i}\\
2yi&=e^{ix}-e^{-ix}\\
2yie^{ix}&=(e^{ix})^2-1\\
(e^{ix})^2-2yie^{ix}-1&=0\\
e^{ix}&=yi\pm\sqrt{1-y^2}\\
ix&=\log(yi\pm\sqrt{1-y^2})\\
x&=-i\log(yi\pm\sqrt{1-y^2})
\end{align}
$y=\cos{x}$とすると,
\begin{align}
y&=\cos{x}\\
&=\frac{e^{ix}+e^{-ix}}{2}\\
2y&=e^{ix}+e^{-ix}\\
2ye^{ix}&=(e^{ix})^2+1\\
(e^{ix})^2-2ye^{ix}+1&=0\\
e^{ix}&=y\pm\sqrt{y^2-1}\\
ix&=\log(y\pm\sqrt{y^2-1})\\
x&=-i\log(y\pm\sqrt{y^2-1})
\end{align}
$y=\tan{x}$とすると,
\begin{align}
y&=\tan{x}\\
&=\frac{\sin{x}}{\cos{x}}\\
&=\frac{(\frac{e^{ix}-e^{-ix}}{2i})}{(\frac{e^{ix}+e^{-ix}}{2})}\\
&=-i\frac{e^{ix}-e^{-ix}}{e^{ix}+e^{-ix}}\\
y(e^{ix}+e^{-ix})&=-i(e^{ix}-e^{-ix})\\
ye^{ix}+ye^{-ix}&=-ie^{ix}+ie^{-ix}\\
ye^{2ix}+y&=-ie^{2ix}+i\\
(i+y)e^{2ix}&=i-y\\
e^{2ix}&=\frac{i-y}{i+y}\\
2ix&=\log\frac{i-y}{i+y}\\
x&=\frac{1}{2i}\log\frac{i-y}{i+y}\\
&=-\frac{i}{2}\log\frac{i-y}{i+y}\\
&=\frac{i}{2}\log\frac{i+y}{i-y}
\end{align}
$\sin^{-1}$と$\cos^{-1}$は解が2つありますが,一般的な定義ではいずれもプラスの方が採用されます.
よって,
\begin{align}
\sin^{-1}x&=-i\log(xi+\sqrt{1-x^2})\\
\cos^{-1}x&=-i\log(x+\sqrt{x^2-1})\\
\tan^{-1}x&=\frac{i}{2}\log\frac{i+x}{i-x}
\end{align}
これらをプログラムで書くと,
Complex complex_asin(Complex x)
{
Complex i;
Complex minus_i;
Complex one;
i.real = 0.0;
i.imag = 1.0;
minus_i.real = 0.0;
minus_i.imag = -1.0;
one.real = 1.0;
one.imag = 0.0;
return complex_multiplication(minus_i, complex_log(complex_addition(complex_multiplication(x, i), complex_sqrt(complex_subtraction(one, complex_multiplication(x, x))))));
}
Complex complex_acos(Complex x)
{
Complex minus_i;
Complex one;
minus_i.real = 0.0;
minus_i.imag = -1.0;
one.real = 1.0;
one.imag = 0.0;
return complex_multiplication(minus_i, complex_log(complex_addition(x, complex_sqrt(complex_subtraction(complex_multiplication(x, x), one)))));
}
Complex complex_atan(Complex x)
{
Complex i;
Complex half_i;
i.real = 0.0;
i.imag = 1.0;
half_i.real = 0.0;
half_i.imag = 0.5;
return complex_multiplication(half_i, complex_log(complex_division(complex_addition(x, i), complex_subtraction(x, i))));
}
以上です.
ソースコードではこの他にも双曲線関数,逆双曲線関数なども実装しているので,ぜひ読んでみて下さい.