この記事ではマルチエージェント深層強化学習における帰納バイアスについて紹介したいと思います。
機械学習の著名な国際学会であるNeurIPSとICMLでは、2024年に、以下の三本の論文がこのトピックに注目しています。
- J. McClellan et al. Boosting Sample Efficiency and Generalization in Multi-agent Reinforcement Learning via Equivariance. NeurIPS, 2024.
- B. Lin and C. Lee. HGAP: Boosting Permutation Invariant and Permutation Equivariant in Multi-Agent Reinforcement Learning via Graph Attention Network. ICML, 2024.
- D. Chen · Q. Zhang. E(3)-Equivariant Actor-Critic Methods for Cooperative Multi-Agent Reinforcement Learning. ICML, 2024.
マルチエージェントのよくある設定
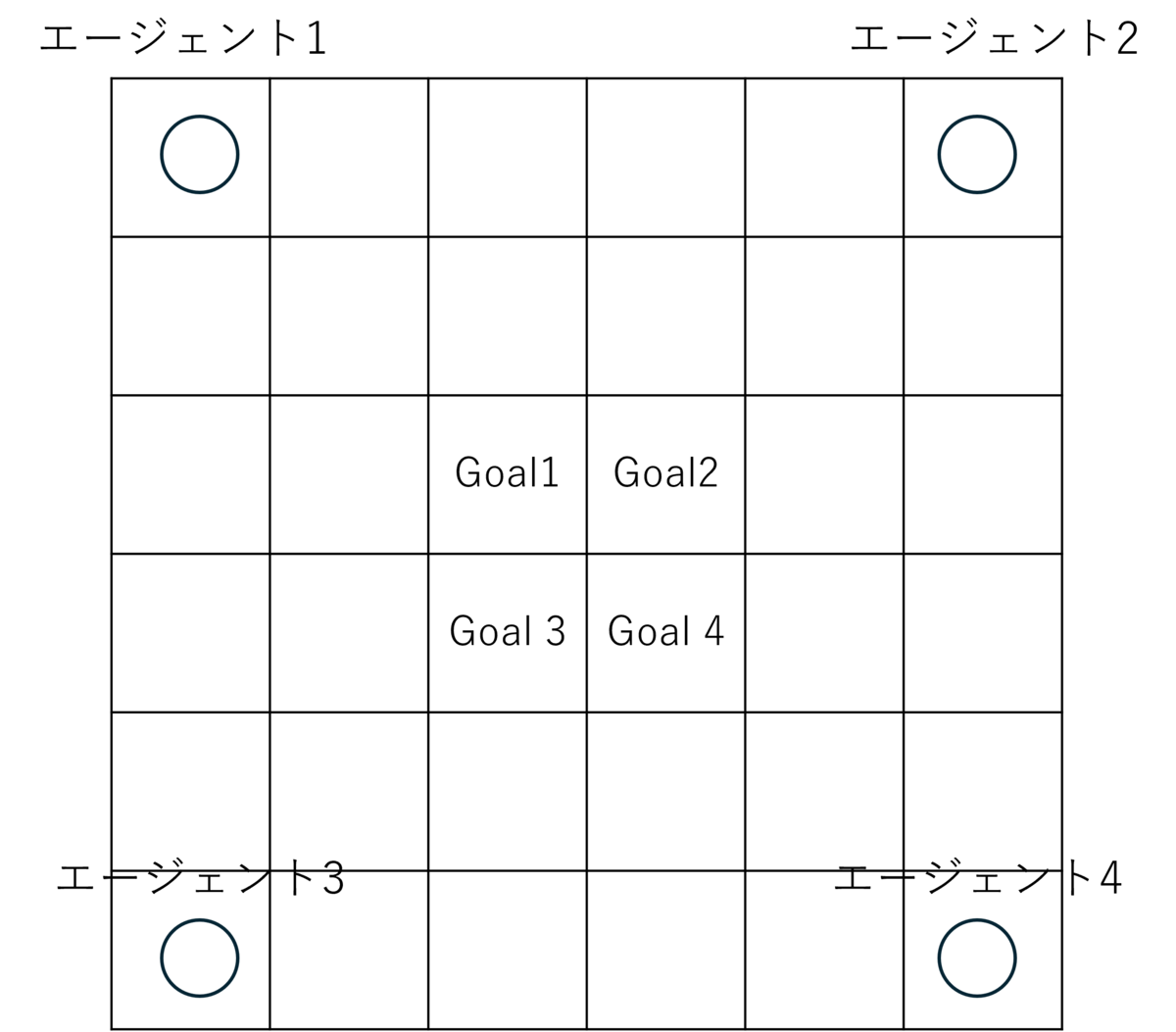
マルチエージェント群を協調制御する際、対称性は一つカギになります。例えば、倉庫ロボットの自動制御を簡素化した下の図を考えたいとします。4つのエージェントがそれぞれのゴールを目指します。エージェント1の最適なルートは「↓↓→→」と動くことです。
次に配置が時計回りに90°回転したものを考えます。
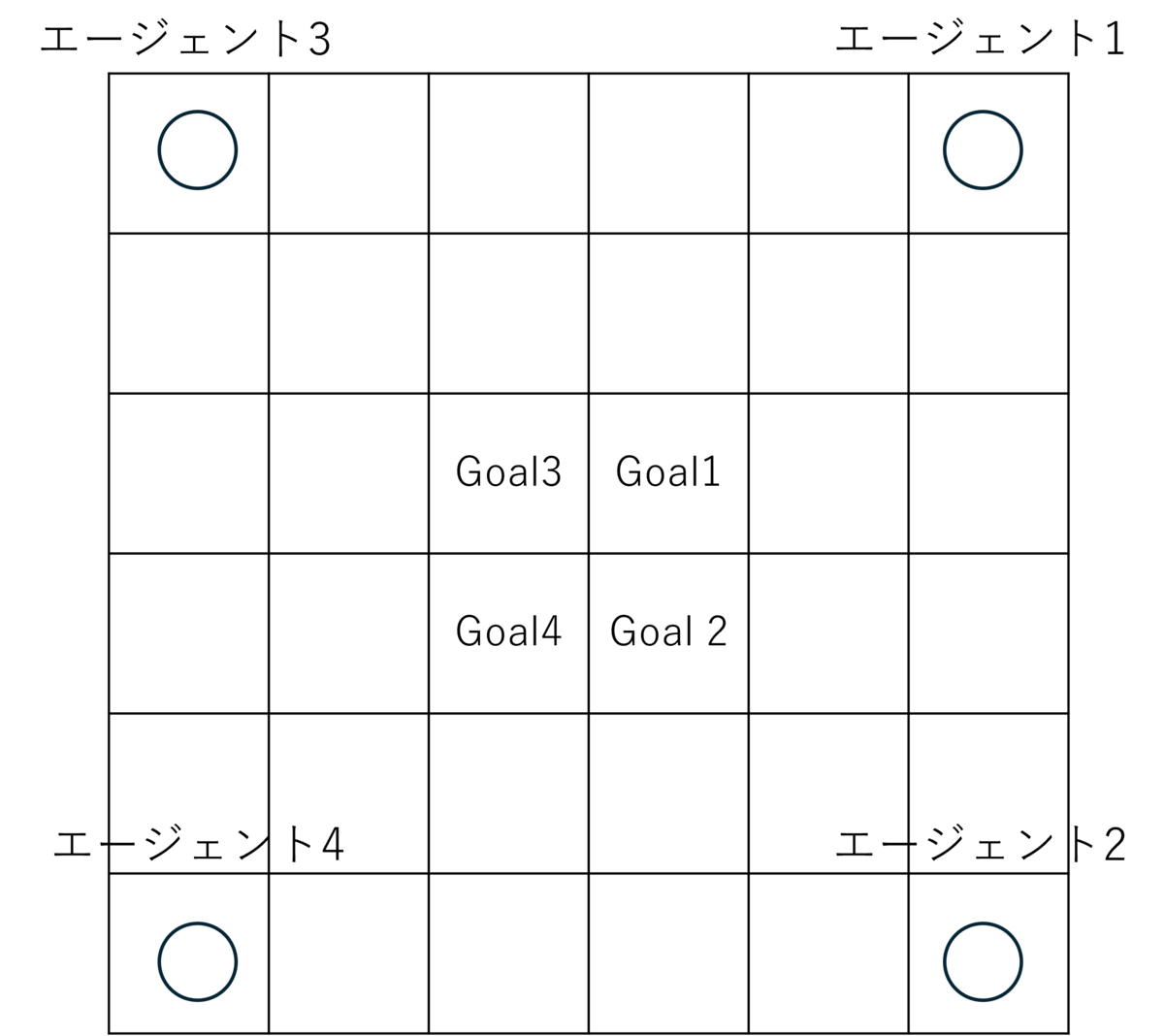
エージェント1の最適なルートは「↓↓←←」です。このルートは90°回転する前のパスと本質的には一緒です。なので90°、180°、270°回転した状態を別個に学習させるのではなく、まとめて学習できれば効率が上がります。
上の倉庫ロボットの制御では点対称性があるように、マルチエージェントのタスクでは回転・平行・鏡映などの変換が起こっても一種の等価性を持ってほしい場合が多々あります。
不変性と同変性
等価性を持ってほしいとは、強化学習の文脈で言うと、「ある観測の変換に対して、その行動出力も"似たように"変換」されてほしいということです。
そのための重要な概念として、不変性と同変性があります。
不変性
特徴量$x$に対してある変換$g(x)$を施すとします。この時、「$g$について、$f$が不変である」とは
f(x) = f(g(x))
であれば、$f$は$g$に対して不変といいます。
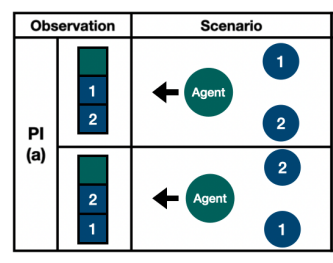
この不変性はマルチエージェントでも出てきます。例えば下図のように、Agentが敵対者①と②から逃げたいという状況を考えます。観測ベクトルが三次元として、一次元目に自分の絶対座標、二次元目に左のセンサ情報、三次元目に右のセンサ情報とします。すると、二つの状況では左右のセンサでどちらの敵対者を観測するかの違いはあるにせよ、左方向に逃げるという状況は変わりません。よって、観測$x$を受け取って行動を決定する$f$は不変性を持ってほしいです。
同変性
特徴量$x$に対してある変換$g(x)$を施すとします。この時、「変換$g$について、$f$が同変である」ならば
f(g(x)) = g'(f(x))
を満たす$g'$が存在します。$g'=g$であることもあります。
これはつまり「入力が変化したならば、出力も入力と同じように変化する」ということです。
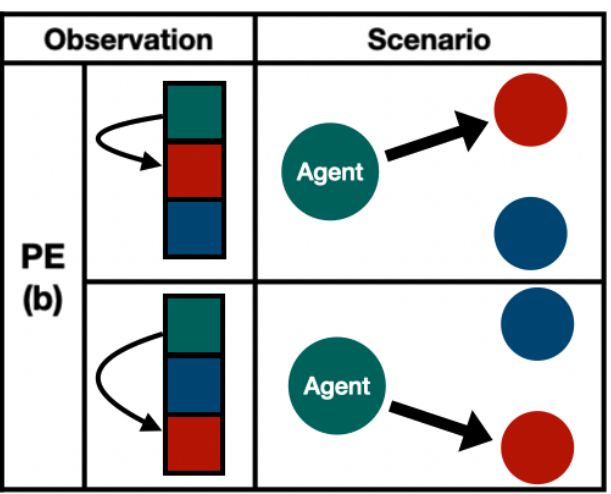
例えば下図のように、Agentが赤い敵対者を攻撃したい状況を考えます。二つの状況は左右のどちらのセンサで敵対者を観測するかの違いがあります。ここでは敵対者を左に観測したら左に攻め、右に観測したら右に攻める、のが理想です。つまり、左から右への変換を$g$としたととき、行動の出力も$f(g(x))$も同様に左から右に変換されてほしいのです(つまり、$g(f(x))$になってほしい)。これはまさしく同変性です。
グラフニューラルネットワークの活用
はじめにあげた論文はどれも何かしら観測の変換に対して同変性・不変性を持つNNモデルの提案を行っています。その中でも、最初の二つはグラフニューラルネットワークを利用しています。
- J. McClellan et al. Boosting Sample Efficiency and Generalization in Multi-agent Reinforcement Learning via Equivariance. NeurIPS, 2024.
- B. Lin and C. Lee. HGAP: Boosting Permutation Invariant and Permutation Equivariant in Multi-Agent Reinforcement Learning via Graph Attention Network. ICML, 2024.
- D. Chen · Q. Zhang. E(3)-Equivariant Actor-Critic Methods for Cooperative Multi-Agent Reinforcement Learning. ICML, 2024.
それでは、最後に、GNNがなぜマルチエージェント深層強化学習と相性がいいのか見てみましょう.
メッセージ伝達
GNNの代表的な定式化にメッセージ伝達によるものがあります。メッセージ伝達型GNNは入力として頂点特徴量付きグラフ $G = (V, E, X)$を受け取り、各頂点を$\mathbb{R}^{d}$に埋め込みます。($V = \left\{1, \ldots, n\right\}$はノードの集合、$E = \{ \{u, v\} | u, v \in V \}$は辺の集合、$\boldsymbol{X}\in\mathbb{R}^{|V| \times d}$は各頂点の$d$次元の特徴量を並べた行列です。)
より具体的には、頂点$v$の特徴量は
\boldsymbol{h}_{v}^{(0)} = \boldsymbol{X}_{v}
から始まり、自分自身の特徴量と隣接頂点の特徴量を使って
\boldsymbol{h}_{v}^{(l + 1)} = f_{\theta, l + 1} \left(\boldsymbol{h}_{v}^{(l)}, \text{隣接頂点集合} \ \{ \boldsymbol{h}_{u}^{(l)} | u \in \mathcal{N}(v) \} \right)
とアップデートしていきます。
メッセージ伝達の同変性
まずグラフの同型性を定義します。
【グラフ同型性】
グラフ$G = (V, E, \boldsymbol{X})$ と $G' = (V', E', \boldsymbol{X}')$が同型であるとは、全単射$f : V \rightarrow V'$が存在し、
X_{v} = \boldsymbol{X}'_{f(v)}
がすべての$v \in V$について成り立ち、かつ、
\{ u, v \} \in E \Leftrightarrow \{ f(u), f(v) \} \in E'
がすべての$u, v \in V$について成り立つことである。
たとえば、下図では$f(1) = 2, f(2) = 3, f(3) = 2, f(4) = 4$という同型写像により、左と右のグラフは同型であると言えます。
メッセージ伝達は同変性と呼ばれる次の性質があります。
【メッセージ伝達の同変性】
メッセージ伝達 $g: (V, E, \boldsymbol{X}) \mapsto \mathbb{R}^{|V| \times d}$は任意の同型なグラフ$G = (V, E, \boldsymbol{X})$と$G' = (V, E, \boldsymbol{X})$、および、任意の同型写像$f: V \rightarrow V'$について、
g(G)_{v} = g(G')_{f(v)}
がすべての$v\in V$について成り立つ。つまり、$G$における頂点$v$の埋め込みは$G'$における頂点$f(v)$の埋め込みと同じということである。
(マルチエージェント)強化学習への応用
同変性があるGNNはマルチエージェント強化学習において力を発揮します。
例えば、上図で左上の緑色のエージェント1(頂点1)だけ他の三つの頂点から離れると高い報酬が得られる状況を考えましょう。左の図では左のセンサーでエージェント2を観測し、右のセンサーではエージェント3を観測します。右の図では、左のセンサーでエージェント3を観測し、右のセンサーでエージェント2を観測します。それぞれのセンサの観測をconcatすると、二つのケースを区別してしまいます。しかし、GNNを使うと二つのケースはどちらもエージェント1の埋め込みは同じになるので、(イメージとしては)学習が二倍に早くなります。
終わり
このブログは株式会社EfficiNet Xのテックブログです。