背景
こんにちは、現在はITインフラを勉強中の人です。
ITインフラについては分かっていないことばかりで日々格闘中です。
ルータについて勉強している中でダイナミックルーティングのOSPFって何なのか、加えて自分が特にん??と思ったことが色々あったので共有として、そしてさらなる理解のために、記事にまとめてみようと思います。
1. OSPF
OSPFとはOpen Shortest Path Firstの略語で自立システムと呼ばれる組織が自身の定める管理ポリシーに従って運用しているルータやネットワークをひとまとめにしたものの中で経路情報を交換するためのプロトコルです。
ダイナミックルーティングのプロトコルは分類の仕方が多くてこんがらがりがちなので簡単にではありますが、数あるダイナミックルーティングプロトコルの中でのOSPFの立ち位置についてまとめてみました。
OSPF
リンクステート型
[ネットワークエンジニアとして:OSPF-Link State Routing](https://www.infraexpert.com/study/ospfz1.html) 上記のサイトが詳しいですが、簡単な要約をするならば、 ルーティングテーブル作成のために丁寧なステップを踏んで通信を確立します。 TCP通信の3wayハンドシェイクの流れと近からずとも遠からずと思っています。IGP
IGPとはInterior Gateway Protocolの略です。 何のInteriorなのかというと、AS(Autonomous System)と呼ばれる自律システムの内側で使われるプロトコルであるからです。 ではASとは何か、ASとはインターネットの管理上のひとまとまりのこと。 Wikipediaでは以下のように書かれているクラスレスルーティングプロトコル
ルータ同士が交換する情報の中にサブネットマスクの情報を含めることができる。 現在の主流はクラスレスルーティングなのでそんなに意識する必要はないかも。。。SPF
Shortest Path Firstつまり最短経路を優先するということ。 OSPFのSPFと同じことを指しています。 OSPFではダイクストラ法というアルゴリズムで最短経路を導きます。OSPFはいくつかの状態を経てインターフェースの情報交換します。
2. ルートの決まり方は?
OSPFでは最短経路を導くためにダイクストラ法(Dijkstra's algorithm)というアルゴリズムを使用しています。
2-1.ダイクストラ法
1959年にオランダ人計算機科学者Edger Wyde Dijkstraが考案した、グラフ理論における最短経路を求めるアルゴリズムの一つです。
乗換案内のアルゴリズムもダイクストラ法で解くことができます。
こういったネットワークグラフを書きスタートからゴールまでの最短経路を導くことができます。
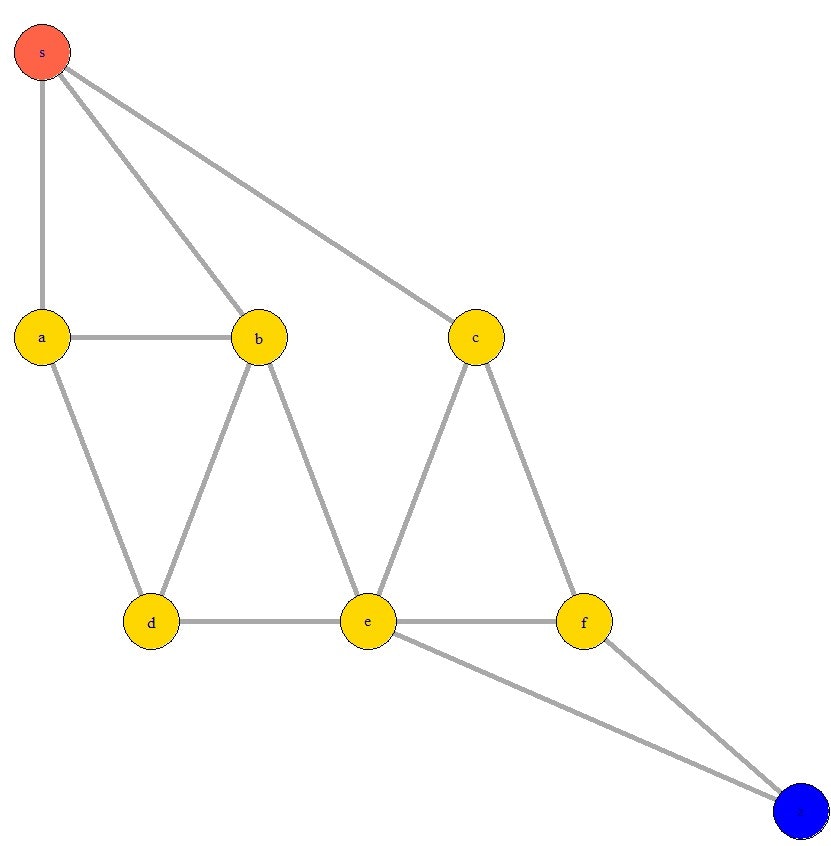
2-1.用語整理
この後の部分で断りなく横文字などを使うため整理をします。
- ノード:ネットワークグラフ上の点を表します。
- エッジ:ネットワークグラフ上のノードを結ぶ線を表します。
- コスト:エッジごとにつけられている重み
わかりにくいですが、乗換案内とOSPFに当てはめて考えてみます。
| 用語 | 乗換案内 | OSPF |
|---|---|---|
| ノード | 駅 | ルータ |
| エッジ | 路線 | ケーブル |
| コスト | 所要時間 | メトリック |
2-2ダイクストラ法の流れ
用語の整理も終わったので、ここからダイクストラ法の流れに入ります。
使うネットワークグラフは以下になります。
(小さいですが、エッジにコストが書いてあります。)
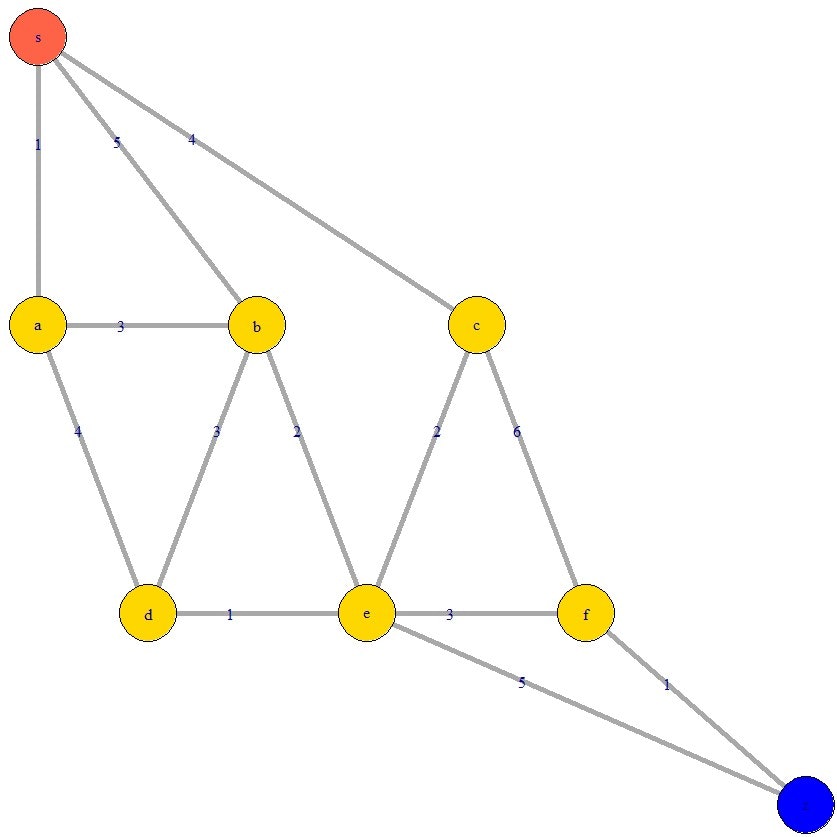
【手順】
- スタート地点とゴール地点を決める
今回は上の図のS点からZ点までの最短経路を考えることにします。(図が小さいので見えない場合はクリックして拡大してください) - スタート地点を選択する
この後の処理の基準となるノードを選択します。
選択したノードの到達コストを0にして到達コストの確定をします。 - スタート地点を除く各ノードまでの到達コスト$\infty$に設定します。
- 選択したノードからエッジで結ばれている各ノードへの到達コストを計算して、それが現在のそれぞれのノードへの到達コストよりも低い場合コストを更新します。
- 未確定のノードの中から最も到達コストの小さいノードを選択し、到達コストを確定します。
- 4.に戻って処理を繰り返します。
正直文章で説明するのには限界があるので、YouTubeにあった解説動画のURLを張っておくので、ぜひ見てみてください。
グラフ理論⑤(ダイクストラのアルゴリズム):予備校のノリで学ぶ「大学数学・物理」
OSPFで考えると、ルータは
3. Rで実装してみる
今回の環境はこちら
- R(ver4.0.0)
- Rstudio desktop(ver1.2.5042)
igraphパッケージにはダイクストラ法をigraphオブジェクトを用いて計算する関数がありますが、今回はそれを使わず、重み付き隣接行列を用いて計算を進めることにします。
# ダイクストラ法
dijkstra <- function(matrix, nstart){
adjacency_matrix <- matrix
adjacency_matrix[which(adjacency_matrix==0)] <- Inf #コストの設定されていないノードへの到達コストを∞にする
diag(adjacency_matrix) <- 0 #対角成分すなわち自身へと回帰する部分のコストを0にする
n <- nrow(matrix) #ノード数
arrival_cost <- rep(Inf, n) #各ノードの到達コストを表すベクトル
arrival_cost[nstart] <- 0 #スタート地点を0に設定(ややこしいのは各ノードをラベルで扱っているため)
unknown_node <- 1:n #未確定ノードを表すベクトル
unknown_node <- unknown_node[-nstart] #スタート地点の削除
selected_node <- nstart #最初に選択されるノードはスタート地点
while(length(unknown_node) > 0){
# イテレータは行列の列指定で使うのでjにしてあります。
for(j in 1:n)
#ここのfor文で中括弧を打つとなぜか通らなくなる(理由は不明、わかる方是非教えてください)
arrival_cost[j]<-min(arrival_cost[j],arrival_cost[selected_node]+adjacency_matrix[selected_node,j])
# 未確定ノードの中から最も到達コストの低いノードを選択する
selected_node<-unknown_node[which(arrival_cost[unknown_node]==min(arrival_cost[unknown_node]))[1]]
# 選択されたノードを確定とし、未確定ノードから削除する
unknown_node <- unknown_node[-which(unknown_node == selected_node)]
}
# 各ノードへの距離が入ったベクトルを出す。
arrival_cost
}
ふう...
長いですね。
上記のコードはこちらのブログを参照にして、変数名を自分がわかるものにしています。
グラフ・ネットワーク分析で遊ぶ(1):グラフ可視化・描画手法
アルゴリズムにかなり寄りましたが、本題に戻ってOSPFがルータ間の最短経路をどのように導くかを確認していきます。
OSPFのルータ間のネットワークに一定の向きがあることはまあ稀なので、今回は無向グラフで作ります。
【ネットワークの概要】
s, a, b, c, d ,e, f, zとラベル付けされた7台のルータがあり
それぞれがOSPFを有効にしている状態です。
AD値をはじめとする設定値はデフォルト、DR,BDRについては今回は割愛します。
ここでルータsからルータzまでの最短経路がどのようになるかを考えます。
OSPFのメトリックは100M/帯域幅となり、これが距離に相当します。
# 重み付き隣接行列の作成
network_matrix<-matrix(c(
# s, a, b, c, d, e, f, z
0, 1, 5, 4, 0, 0, 0, 0, #s
1, 0, 3, 0, 4, 0, 0, 0, #a
5, 3, 0, 0, 3, 2, 0, 0, #b
4, 0, 0, 0, 0, 2, 6, 0, #c
0, 4, 3, 0, 0, 1, 0, 0, #d
0, 0, 2, 2, 1, 0, 3, 5, #e
0, 0, 0, 6, 0, 3, 0, 1, #f
0, 0, 0, 0, 0, 5, 1, 0 #z
),
ncol = 8, nrow = 8,byrow = TRUE)
# 隣接行列はネットワーク図の隣接関係(ネイバー)を行列の形式で表したものです。
# network_matrix[1, 4]は1番目のノード(ルータ)sから4番目のノード(ルータ)cまでの距離(メトリック)を表しています。
# 1番目のルータsからの最短距離を求める
dijkstra(network_matrix, 1)
実行結果がこちら
# s, a, b, c, d, e, f, z
[1] 0 1 4 4 5 6 9 10
これは、スタート地点に指定したルータから各ルータまでの最短のメトリックを表しています。
なのでルータsからルータzまでの最短経路はそのメトリックが10となる以下の経路になります。
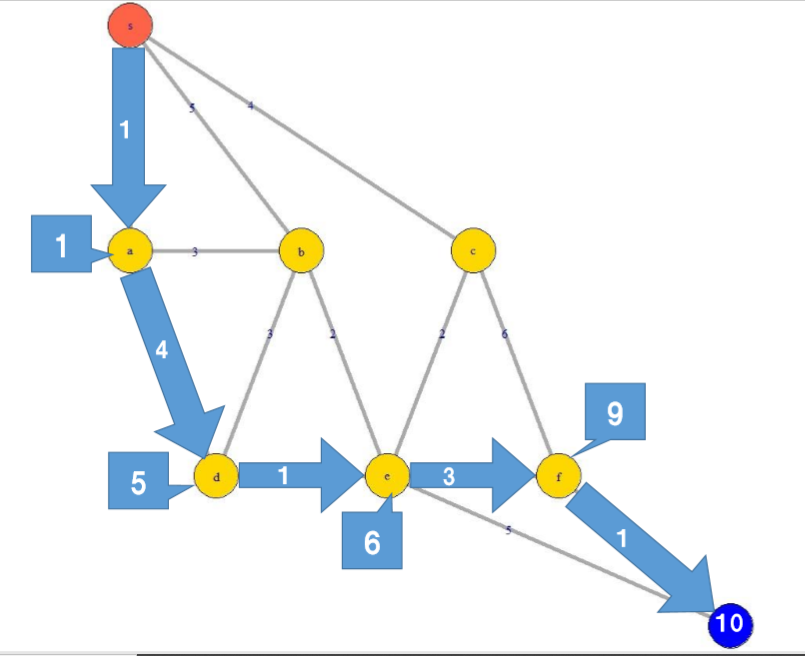
ダラダラと長く書いてしまいましたが、読んでいただきありがとうございました。
指摘等ありましたら、是非コメントでお願いします。
適宜更新します。