LoginSignup
10
4

More than 3 years have passed since last update.

@Ebishu

三角形の頂点の座標から五心の座標を求める

Last updated at Posted at 2020-07-14

1. 準備

点を扱う struct があると便利なので定義します。

struct Point {
    double x, y;

    Point() = default;
    Point(double x_, double y_): x(x_), y(y_) {}

    Point operator+(const Point& rhs) const { return Point(x + rhs.x, y + rhs.y); }
    Point operator-(const Point& rhs) const { return Point(x - rhs.x, y - rhs.y); }
    Point operator*(double scalar) const { return Point(x * scalar, y * scalar); }
    Point operator/(double scalar) const { return Point(x / scalar, y / scalar); }

    double length() const { return std::sqrt(lengthSq()); }
    double lengthSq() const { return x * x + y * y; }
    double distanceFrom(const Point& rhs) const { return (*this - rhs).length(); }
    double distanceFromSq(const Point& rhs) const { return (*this - rhs).lengthSq(); }

    friend Point operator*(double scalar, const Point& rhs) { return Point(scalar * rhs.x, scalar * rhs.y); }
    friend std::istream& operator>>(std::istream& is, Point& rhs) { return is >> rhs.x >> rhs.y; }
};

次に三角形を扱う struct を定義します。今回はこれに五心の座標を求めるメンバ関数を追加していきます。

struct Triangle {
    Point a, b, c;

    Triangle(const Point& a_, const Point& b_, const Point& c_) :a(a_), b(b_), c(c_) {}

    double getAngleA() const {
        double
            dist_a = b.distanceFrom(c),
            dist_b = c.distanceFrom(a),
            dist_c = a.distanceFrom(b);
        return std::acos((-dist_a * dist_a + dist_b * dist_b + dist_c * dist_c) / (2 * dist_b * dist_c));
    }

    double getAngleB() const {
        double
            dist_a = b.distanceFrom(c),
            dist_b = c.distanceFrom(a),
            dist_c = a.distanceFrom(b);
        return std::acos((dist_a * dist_a - dist_b * dist_b + dist_c * dist_c) / (2 * dist_c * dist_a));
    }

    double getAngleC() const { return std::acos(-1.0) - getAngleA() - getAngleB(); }

    friend std::istream& operator>>(std::istream& is, Triangle& rhs) { return is >> rhs.a >> rhs.b >> rhs.c; }
};

また、これとは別に
$\rm\triangle ABC$ と点 $\rm P$ があり、面積比が $\triangle{\rm PBC}:\triangle{\rm PCA}:\triangle{\rm PAB}=p:q:r$ の時、$\rm P$ の位置ベクトルを計算しておきます。

  • $\rm P$ が $\rm\triangle ABC$ の内部の場合
    条件より、$$p\overrightarrow{\rm PA}+q\overrightarrow{\rm PB}+r\overrightarrow{\rm PC}=\vec{0}$$が成立します。(こちらのサイトを参照）したがって、$$\vec p=\frac{p\vec a+q\vec b+r\vec c}{p+q+r}\tag1$$

  • 外部の場合

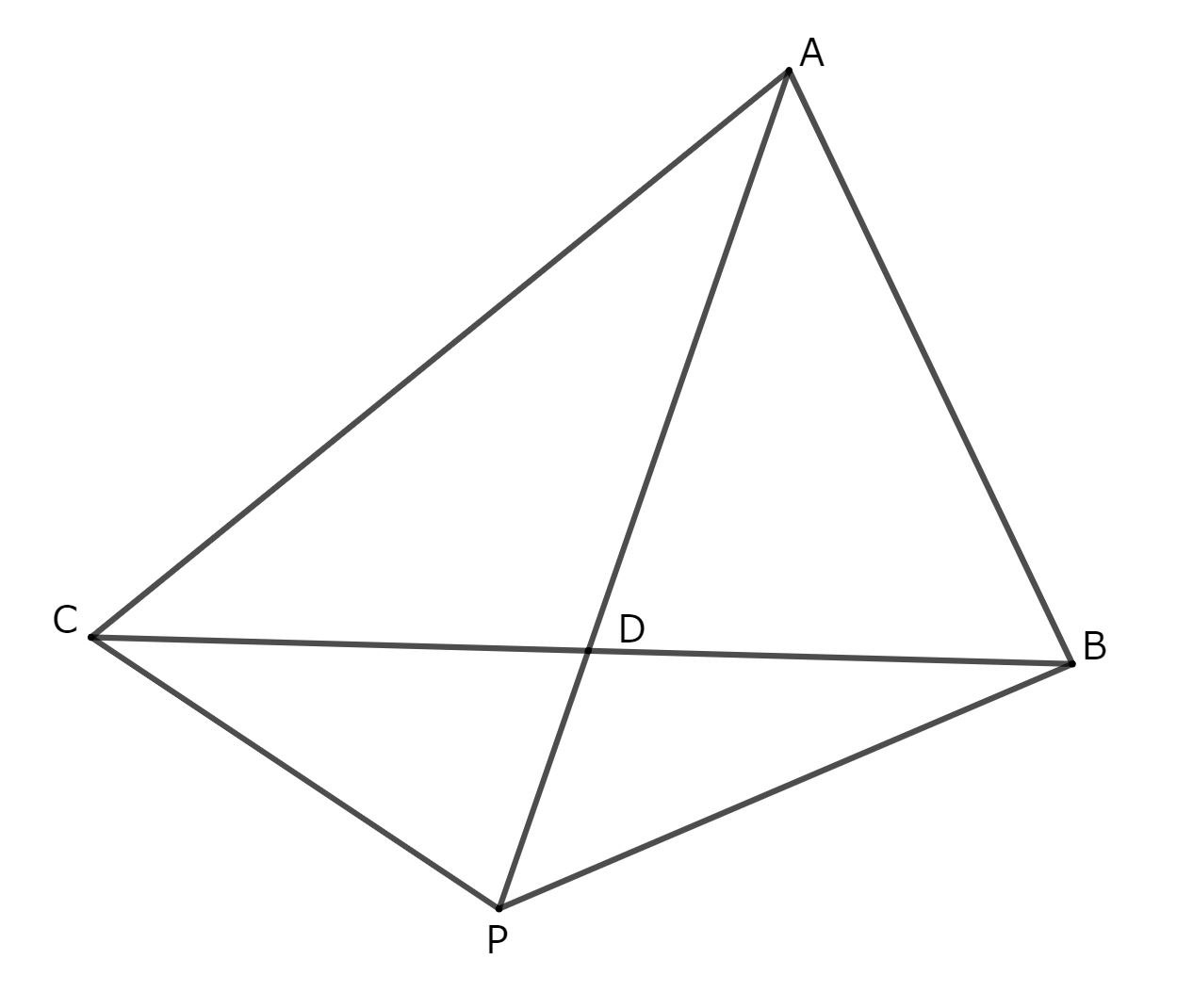
    上図の場合を考えます。このとき、${\rm BD:CD}=r:q$ なので、$$\vec d=\frac{q\vec b+r\vec c}{q+r}$$また、${\rm\triangle ABC:\triangle PBC}=q+r-p:p$ なので、$${\rm AD:PD}=(q+r-p):p$$よって、点 $\rm P$ は $\rm AD$ を $q+r:p$ に外分する点なので、$$\vec p=\frac{-p\vec a+(q+r)\vec d}{-p+q+r}$$$$=\frac{-p\vec a+(q+r)\frac{q\vec b+r\vec c}{q+r}}{-p+q+r}$$$$=\frac{-p\vec a+q\vec b+r\vec c}{-p+q+r}\tag2$$

2. コード

重心

一番簡単です。

Point getCentroid() const {
    return (a + b + c) / 3;
}

外心

$\rm\triangle ABC$ の外心 $\rm O$ の位置ベクトルを計算します。

$\rm\triangle BPC,\triangle CPA,\triangle APB$ の面積をそれぞれ $p,q,r$、$\angle{\rm BAC}=\alpha,\angle{\rm CBA}=\beta,\angle{\rm ACB}=\gamma$、外接円の半径を $R$ とおきます。

  • $\rm O$ が $\rm\triangle ABC$ の内部にある場合
    円周角の定理より $\angle{\rm BPC}=2\alpha$ なので、$$p=\frac12R^2\sin2\alpha$$同様にして
    $$q=\frac12R^2\sin2\beta, r=\frac12R^2\sin2\gamma$$よって、$$p:q:r=\sin2\alpha:\sin2\beta:\sin2\gamma$$
    したがって、$(1)$より、$$\vec{o}=\frac{\sin2\alpha\vec a+\sin2\beta\vec b+\sin2\gamma\vec c}{\sin2\alpha+\sin2\beta+\sin2\gamma}$$

  • 外部の場合
    $$q=\frac12R^2\sin2\beta,r=\frac12R^2\sin2\gamma$$内角 $\angle{\rm BPC}=2\pi-2\alpha$ なので、$$p=\frac12R^2\sin(2\pi-2\alpha)=-\frac12R^2\sin2\alpha$$したがって、$(2)$より、$$\vec{o}=\frac{-(-\sin2\alpha\vec a)+\sin2\beta\vec b+\sin2\gamma\vec c}{-(-\sin2\alpha)+\sin2\beta+\sin2\gamma}$$$$=\frac{\sin2\alpha\vec a+\sin2\beta\vec b+\sin2\gamma\vec c}{\sin2\alpha+\sin2\beta+\sin2\gamma}$$

Point getCircumCenter() const {
    double
        sin2a = std::sin(2 * getAngleA()),
        sin2b = std::sin(2 * getAngleB()),
        sin2c = std::sin(2 * getAngleC());
    return (sin2a * a + sin2b * b + sin2c * c) / (sin2a + sin2b + sin2c);
}

【追記】 角度で計算すると誤差が大きくなってしまうので、長さに変えて計算する方が良いです。

Point getCircumCenter() const {
    double
        d_a = (b - c).lengthSq(),
        d_b = (c - a).lengthSq(),
        d_c = (a - b).lengthSq(),
        t_a = d_a * (-d_a + d_b + d_c),
        t_b = d_b * (d_a - d_b + d_c),
        t_c = d_c * (d_a + d_b - d_c),
        s = t_a + t_b + t_c;

    return t_a / s * a + t_b / s * b + t_c / s * c;
}

内心

同様に、位置ベクトルを計算します。
$\rm\triangle ABC$ の内心を $\rm I$、内接円の半径を $r$ とおくと、$$\triangle{\rm BIC}=\frac12ar,\triangle{\rm CIA}=\frac12br,\triangle{\rm AIB}=\frac12cr$$となるので、$${\rm \triangle BIC:\triangle CIA:\triangle AIB}=a: b:c$$となります。したがって、$(1)$より、$$\vec i=\frac{a\vec a+b\vec b+c\vec c}{a+b+c}$$

Point getInnerCenter() const {
    double
        dist_a = b.distanceFrom(c),
        dist_b = c.distanceFrom(a),
        dist_c = a.distanceFrom(b);
    return (dist_a * a + dist_b * b + dist_c * c) / (dist_a + dist_b + dist_c);
}

垂心

同様に、位置ベクトルを計算します。
$\rm\triangle ABC$ において、外心を $\rm O$、重心を $\rm G$、垂心を $\rm H$とおくと $\rm{O,G,H}$ は一直線上にあり,$${\rm OG:GH}=1:2$$が成立する（オイラー線）ので、$$\vec g=\frac{2\vec o+\vec h}3$$よって、$$\vec h=3\vec g-2\vec o$$

Point getOrthoCenter() const {
    return a + b + c - 2 * getCircumCenter();
}

傍心

同様に、位置ベクトルを計算します。

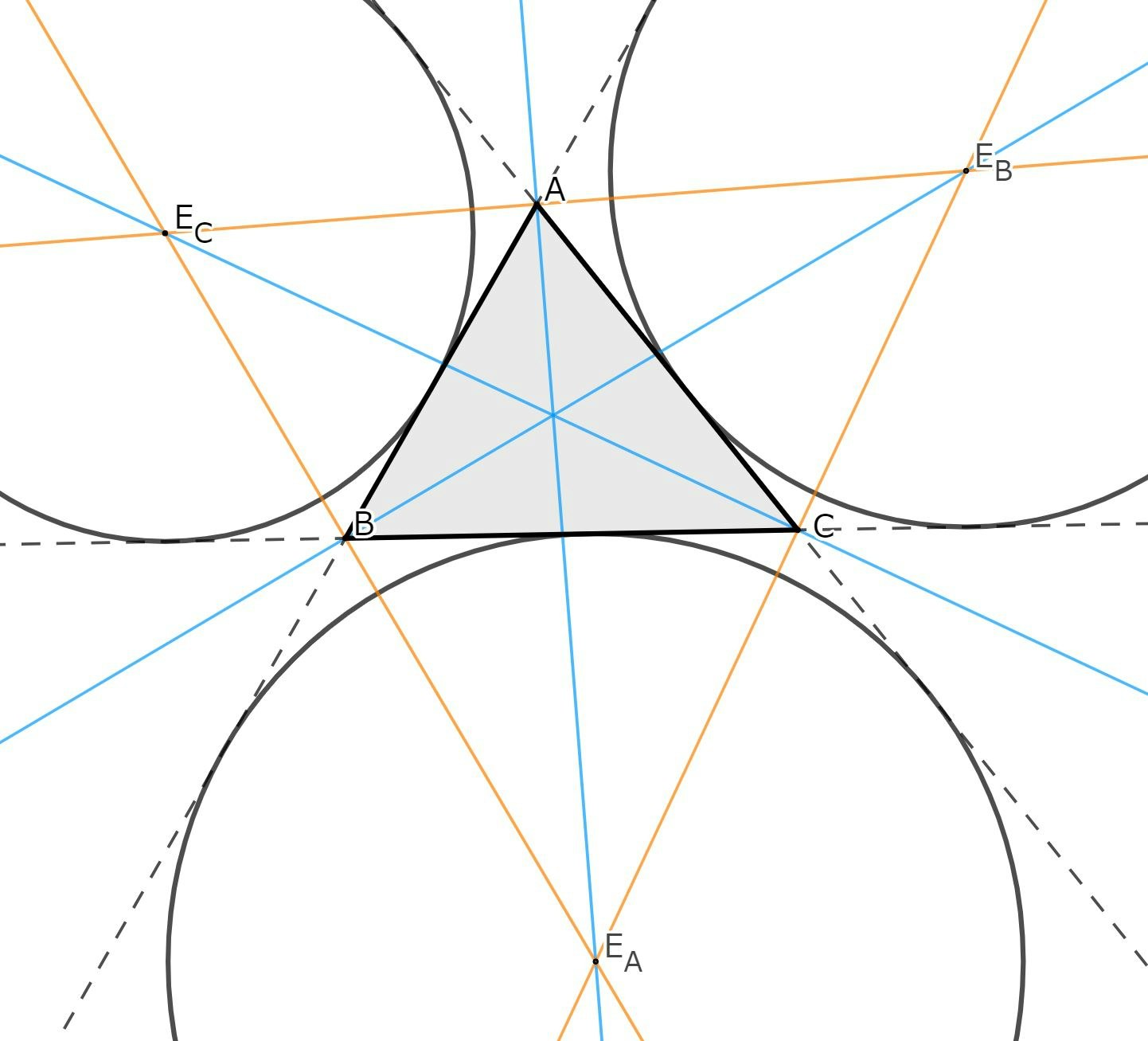
上図のように $\rm\triangle ABC$ に対して傍心 $\rm E_A,E_B,E_C$ をそれぞれおきます。接線はその接点を通る半径に垂直なので、$${\rm\triangle E_ABC:\triangle E_ACA:\triangle E_AAB}=a: b:c$$したがって、$(2)$ より、$$\overrightarrow{E_A}=\frac{-a\vec a+b\vec b+c\vec c}{-a+b+c}$$同様にして、$$\overrightarrow{E_B}=\frac{a\vec a-b\vec b+c\vec c}{a-b+c}, \overrightarrow{E_C}=\frac{a\vec a+b\vec b-c\vec c}{a+b-c}$$

Point getExcenterA() const {
    double
        dist_a = b.distanceFrom(c),
        dist_b = c.distanceFrom(a),
        dist_c = a.distanceFrom(b);
    return (-dist_a * a + dist_b * b + dist_c * c) / (-dist_a + dist_b + dist_c);
}

Point getExcenterB() const {
    double
        dist_a = b.distanceFrom(c),
        dist_b = c.distanceFrom(a),
        dist_c = a.distanceFrom(b);
    return (dist_a * a - dist_b * b + dist_c * c) / (dist_a - dist_b + dist_c);
}

Point getExcenterC() const {
    double
        dist_a = b.distanceFrom(c),
        dist_b = c.distanceFrom(a),
        dist_c = a.distanceFrom(b);
    return (dist_a * a + dist_b * b - dist_c * c) / (dist_a + dist_b - dist_c);
}

3. まとめ

これらをまとめたコードです。

struct Point {
    double x, y;

    Point() = default;
    Point(double x, double y)
        : x(x_)
        , y(y_) {}

    Point operator+(const Point& rhs) const { return Point(x + rhs.x, y + rhs.y); }
    Point operator-(const Point& rhs) const { return Point(x - rhs.x, y - rhs.y); }
    Point operator*(double scalar) const { return Point(x * scalar, y * scalar); }
    Point operator/(double scalar) const { return Point(x / scalar, y / scalar); }

    double length() const { return std::sqrt(lengthSq()); }
    double lengthSq() const { return x * x + y * y; }
    double distanceFrom(const Point& rhs) const { return (*this - rhs).length(); }
    double distanceFromSq(const Point& rhs) const { return (*this - rhs).lengthSq(); }

    friend Point operator*(double scalar, const Point& rhs) { return Point(scalar * rhs.x, scalar * rhs.y); }
    friend std::istream& operator>>(std::istream& is, Point& rhs) { return is >> rhs.x >> rhs.y; }
};

struct Triangle {
    Point a, b, c;

    Triangle(const Point& a, const Point& b, const Point& c)
        : a(a)
        , b(b)
        , c(c) {}

    double getAngleA() const {
        double
            dist_a = b.distanceFrom(c),
            dist_b = c.distanceFrom(a),
            dist_c = a.distanceFrom(b);
        return std::acos((-dist_a * dist_a + dist_b * dist_b + dist_c * dist_c) / (2 * dist_b * dist_c));
    }

    double getAngleB() const {
        double
            dist_a = b.distanceFrom(c),
            dist_b = c.distanceFrom(a),
            dist_c = a.distanceFrom(b);
        return std::acos((dist_a * dist_a - dist_b * dist_b + dist_c * dist_c) / (2 * dist_c * dist_a));
    }

    double getAngleC() const { return std::acos(-1.0) - getAngleA() - getAngleB(); }

    //重心
    Point getCentroid() const {
        return (a + b + c) / 3;
    }

    //外心
    Point getCircumCenter() const {
        double
            d_a = (b - c).lengthSq(),
            d_b = (c - a).lengthSq(),
            d_c = (a - b).lengthSq(),
            t_a = d_a * (-d_a + d_b + d_c),
            t_b = d_b * (d_a - d_b + d_c),
            t_c = d_c * (d_a + d_b - d_c),
            s = t_a + t_b + t_c;

        return t_a / s * a + t_b / s * b + t_c / s * c;
    }

    //内心
    Point getInnerCenter() const {
        double 
            dist_a = b.distanceFrom(c),
            dist_b = c.distanceFrom(a),
            dist_c = a.distanceFrom(b);
        return (dist_a * a + dist_b * b + dist_c * c) / (dist_a + dist_b + dist_c);
    }

    //垂心
    Point getOrthoCenter() const {
        return a + b + c - 2 * getCircumCenter();
    }

    //傍心 A
    Point getExcenterA() const {
        double
            dist_a = b.distanceFrom(c),
            dist_b = c.distanceFrom(a),
            dist_c = a.distanceFrom(b);
        return (-dist_a * a + dist_b * b + dist_c * c) / (-dist_a + dist_b + dist_c);
    }

    //傍心 B
    Point getExcenterB() const {
        double
            dist_a = b.distanceFrom(c),
            dist_b = c.distanceFrom(a),
            dist_c = a.distanceFrom(b);
        return (dist_a * a - dist_b * b + dist_c * c) / (dist_a - dist_b + dist_c);
    }

    //傍心 C
    Point getExcenterC() const {
        double
            dist_a = b.distanceFrom(c),
            dist_b = c.distanceFrom(a),
            dist_c = a.distanceFrom(b);
        return (dist_a * a + dist_b * b - dist_c * c) / (dist_a + dist_b - dist_c);
    }

    friend std::istream& operator>>(std::istream& is, Triangle& rhs) { return is >> rhs.a >> rhs.b >> rhs.c; }
};
10
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
10
4