Squircle の実装

はじめに

OpenSiv3D Challenge 2021 Challenge 5 として、Squircle を Shape2D で作成できるようにしました。この記事では、完成までの流れを説明します。

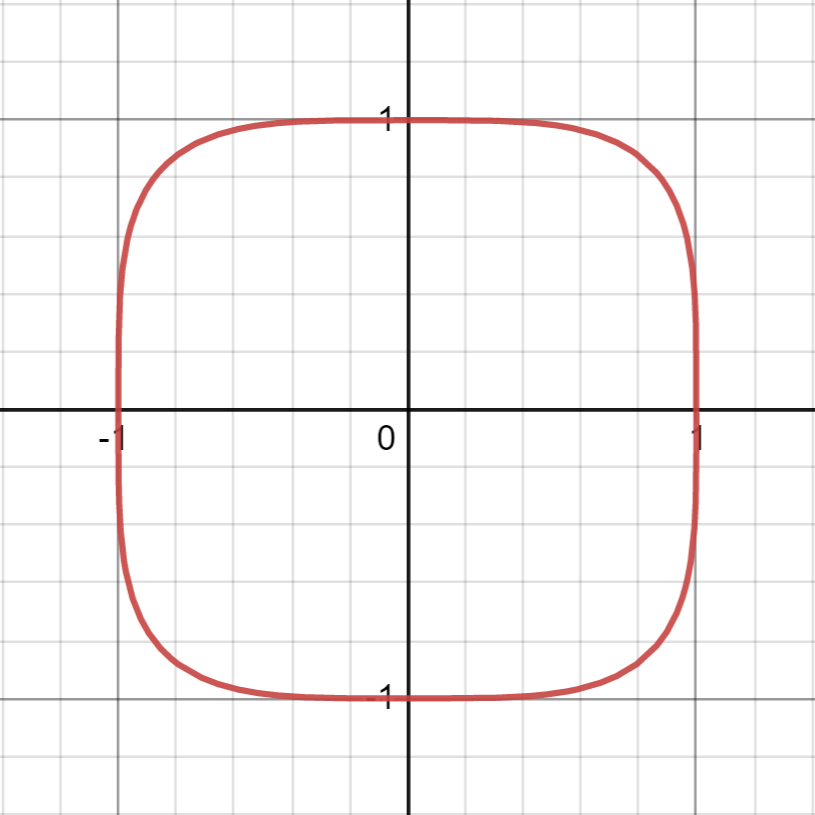
Squircle とは

Squircle (wiki: https://en.wikipedia.org/wiki/Squircle) とは、円と正方形の中間のような図形です。角丸四角形に似ていますが、角丸四角形よりも滑らかなであることが特徴です。数式で表現すると、直交座標系で
$$x^4+y^4=1$$ 極座標系で$$r=\frac{1}{\left(\cos^4\theta+\sin^4\theta\right)^\frac{1}{4}}$$となります。

最初の案

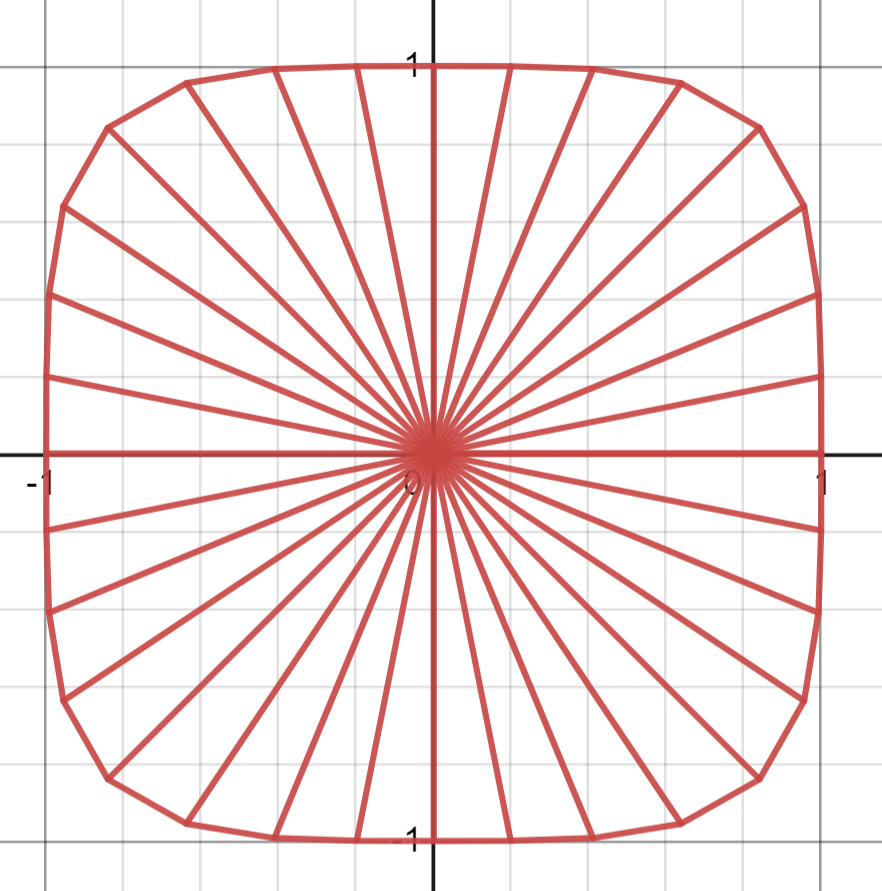
一番目の案は Ryoga.exe さんによる、角度で分割する方法でした。頂点数=32のときは次のようになります。

これを見ると、丸いところと真っ直ぐなところに同じぐらい頂点が割り振られていることが分かります。Squircle の形状を考えると、丸いところに頂点を割り振ってカクつきをなるべく抑えたいです。さらに、割り振るときの座標計算は、なるべく軽くしたいです。

私の案

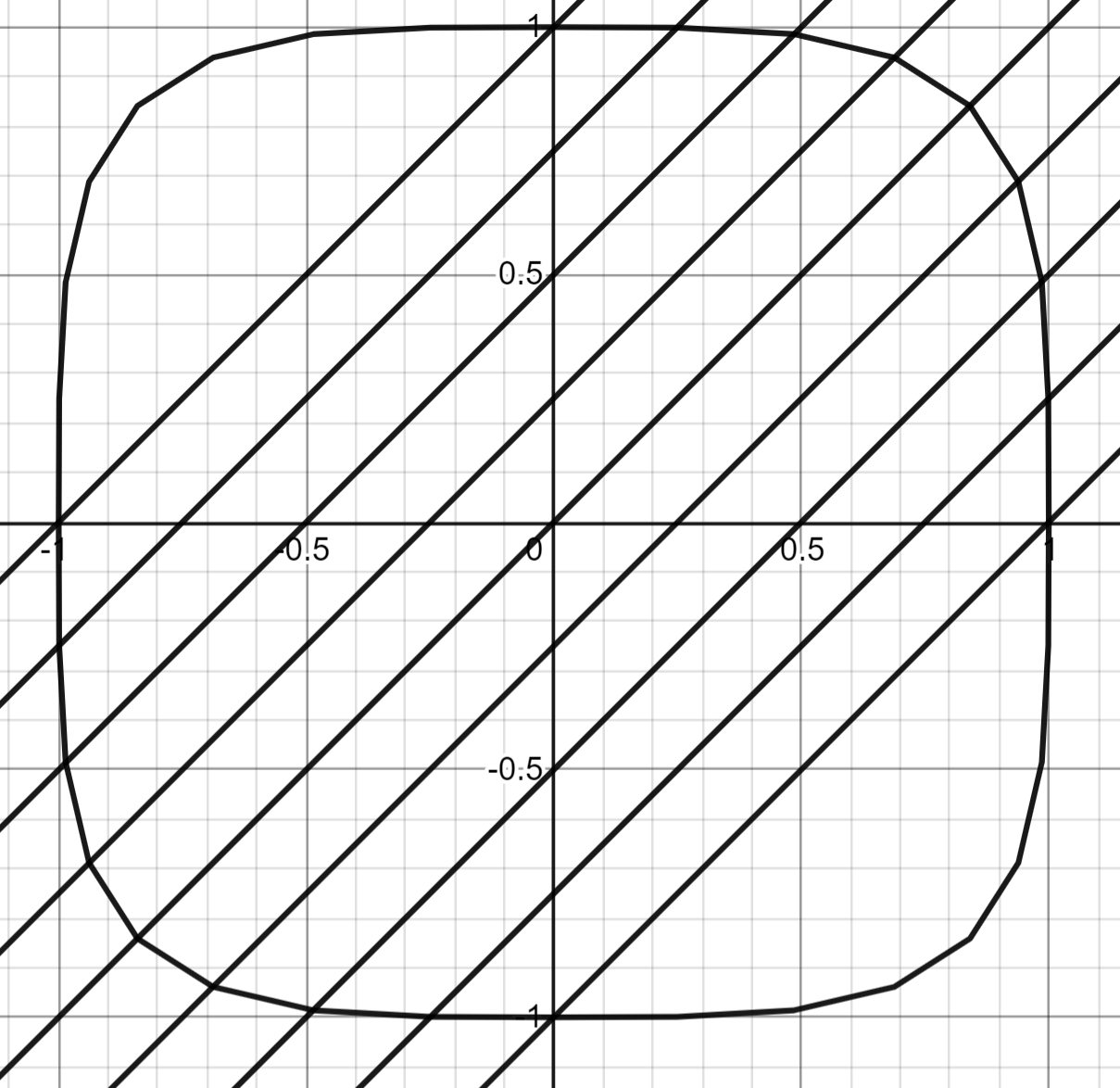
そこで、対角線との交点で区切る、という方法を考えました。頂点数=32のときは次のようになります。

丸いところでは対角線に対して平行に近くなるので頂点がより多く集まり、真っ直ぐなところでは対角線に対して斜め(45°)になるので頂点があまり割り振られない、という仕組みです。

比較

では、この二つの分割を比較してみましょう。頂点数=24のとき、それぞれの分割は以下のようになります。左が角度による分割、右が対角線による分割です。

確かに、対角線による分割の方が、同じ頂点数でも丸いところにより多く割り振られていることが分かります。

計算

では、対角線による分割を計算していきます。
まず、$(x,y)\rightarrow(x+y,x-y)$ という変換によりSquircleを $45^\circ$回転($1/\sqrt{2}$ 倍に縮小) させます。これをすると、対角線は $x$ 軸 / $y$ 軸に平行となるので、計算がしやすいです。このとき、Squircleの式は
$$x^4+6x^2y^2+y^4=\frac{1}{2}$$
となります。ここで、この式を $y^2$ についての方程式とみると
$$y=\pm\sqrt{-3x^2+\sqrt{8x^4+\frac{1}{2}}}$$
となり、この式に $x$ 座標の値を代入することで、$45^\circ$回転後の点の座標が分かり、この座標に逆変換を施すことで、回転前のSquircleを分割したときの座標が求まります。
この式は四則演算と平方根だけが登場しているため、計算も軽くて良いです。

実装

座標の計算ができたので、いよいよ実装に移ります。
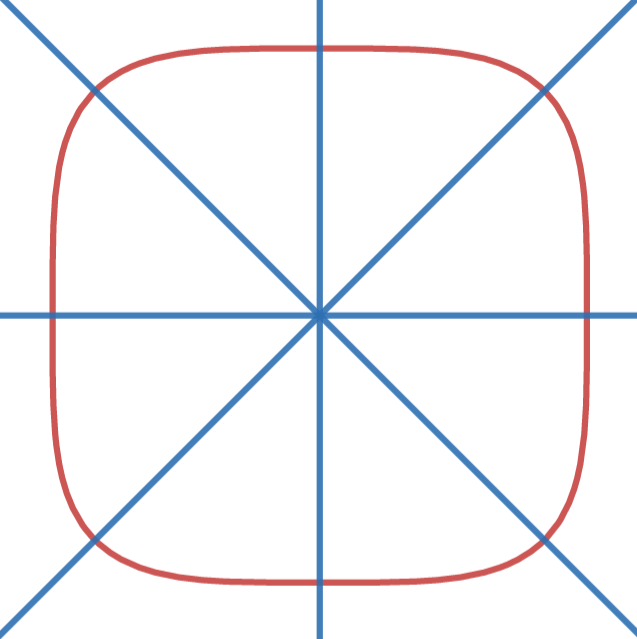
さて、Squircle を N 分割するので、当然座標の計算は N 回かかることになります。しかし、見てもわかるように Squircle には対称性があります。なるべく高速に計算するためには、この対称性を使わない手はないです。

このように、Squircle は 8 等分することができます。よって、そのうちどれか 1 つについて分割したときの座標を計算すれば、全体も計算できるわけです。これにより、計算回数を 1/8 に削減できました！コードは以下になります。1/8 を計算→1/4 を計算→1/2 を計算→全体を計算という流れになっています。

// 8 の倍数
const uint32 n = quality - quality % 8 + 8;

Array<Float2> vertices(n / 8 + 1);

for (uint32 i = 0; i <= n / 8; ++i)
{
    const double x = (n / 8 - i) * 4.0 / n;
    const double y = std::sqrt(-3 * x * x + std::sqrt(8 * x * x * x * x + 0.5));

    vertices[i] = { -x + y, -x - y };
}

for (uint32 i = n / 8 - 1; i >= 1; --i)
{
    vertices.emplace_back(-vertices[i].y, -vertices[i].x);
}

for (uint32 i = 0; i < n / 4; ++i)
{
    vertices.emplace_back(-vertices[i].y, vertices[i].x);
}

for (uint32 i = 0; i < n / 2; ++i)
{
    vertices.emplace_back(-vertices[i].x, -vertices[i].y);
}

Reputeless さんによる改善

Ebishu さんの改良点としては、emplace_back() や push_back() は毎回 capacity チェックをして、足りない場合にメモリの再確保をするので、
最初に全要素分のサイズを確保して代入で入れたほうが良いです。

その通りです（ありがとうございます）。そこで、最初にサイズを確保して代入するように改善したコードが以下となります。

// 8 の倍数
const uint32 n = (quality + 7) / 8 * 8;

Array<Float2> vertices(n);
Float2* pPos = vertices.data();

for (uint32 i = 0; i <= n / 8; ++i)
{
    // 45°回転してから, x 座標を n/8 分割
    // 計算: https://www.desmos.com/calculator/0wrmga2lfk?lang=ja

    const float x = (n / 8 - i) * 4.0f / n;
    const float y = std::sqrtf(-3 * x * x + std::sqrtf(8 * x * x * x * x + 0.5f));

    pPos->x = -x + y;
    pPos->y = -x - y;
    ++pPos;
}

for (uint32 i = n / 8 - 1; i >= 1; --i)
{
    pPos->x = -vertices[i].y;
    pPos->y = -vertices[i].x;
    ++pPos;
}

for (uint32 i = 0; i < n / 4; ++i)
{
    pPos->x = -vertices[i].y;
    pPos->y = vertices[i].x;
    ++pPos;
}

for (uint32 i = 0; i < n / 2; ++i)
{
    pPos->x = -vertices[i].x;
    pPos->y = -vertices[i].y;
    ++pPos;
}

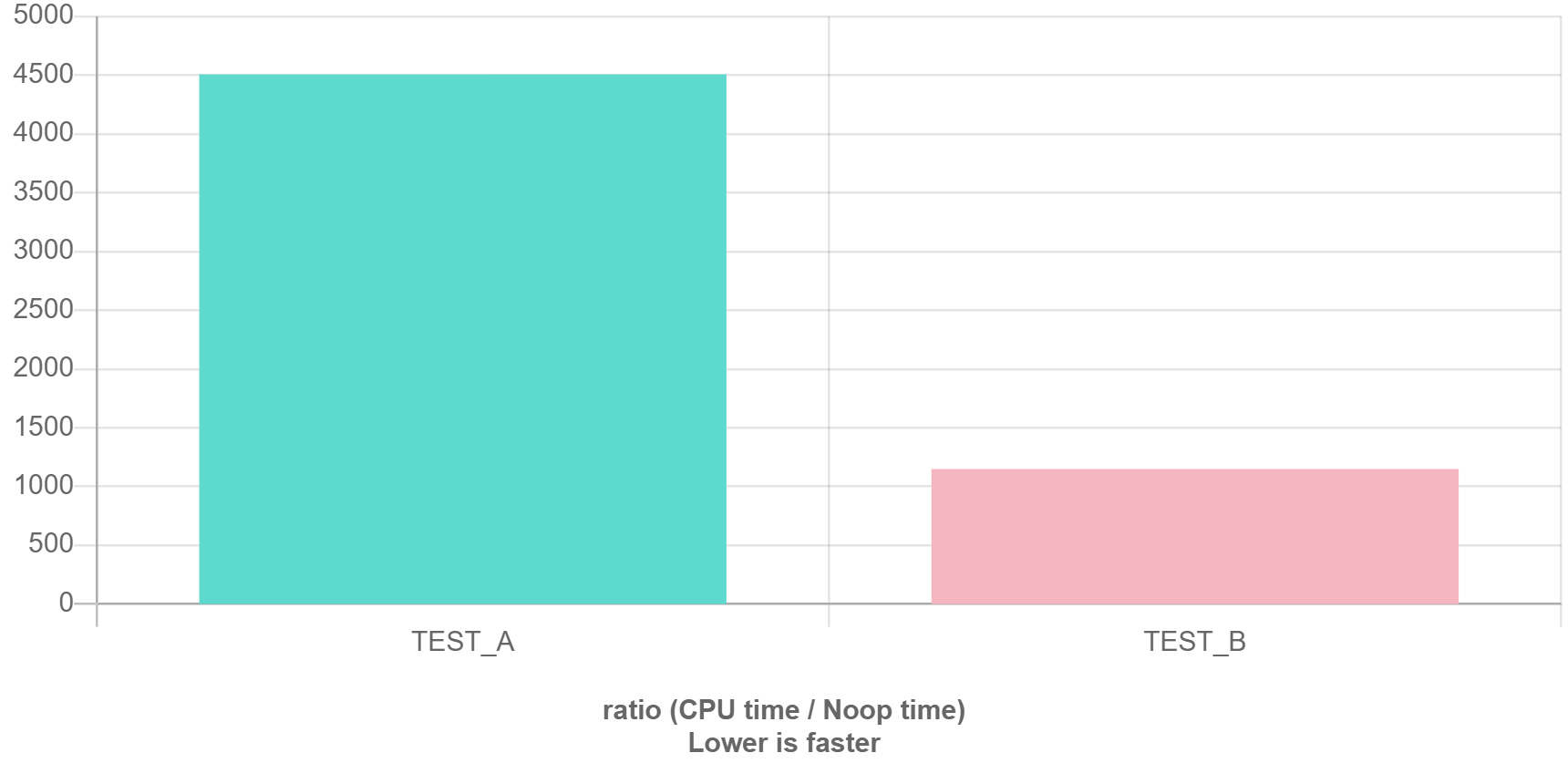
Quick C++ Benchmark で計測をした結果がこちらです。TEST_A が改善前、TEST_B が改善後を表しています。

圧倒的ですね！

まとめ

今年の3月から5月にかけて、OpenSiv3D Challenge 2021 Challenge 5 に参加し、Shape2D::Squircleを完成・commit しました。OpenSiv3D Challenge 2021 を開始してくださった Reputeless さん、実装案を共有してくださった Ryoga.exe さん、ありがとうございます。
github の commit はここから見ることができます: https://github.com/Siv3D/OpenSiv3D/commit/00fe7101a8b8460313399f84494ec4d3a564707a

別の Squircle?

英語版 Wikipedia を読むと、Fernández–Guasti squircle と呼ばれる別の Squircle があることが分かります。この実装はまだ commit に至っていません。もし興味があれば、OpenSiv3D Challenge 2021 Challenge 5 の Slack にぜひ入ってください！OpenSiv3D の Slack にはここから入ることができます。https://siv3d.github.io/ja-jp/community/community/