#はじめに
YouTubeに
https://www.youtube.com/watch?v=0o7T6Pu0WJs&list=WL&t=205s&index=65
このようなパーフェクトなL-Systemについてのチュートリアルがあったので、自分なりにコメントを追加して解説してみようと思います。
#L-Systemとは
L-Systemについてざっくりと説明します。
L-Systemは、ある文字列を定義した変換規則（ルール）に則り世代を進めどんどん変化させていくことで植物の成長等を表現するアルゴリズムです。
例えば一番最初の世代の文字列をAとします。
Aの変換規則を**「AB」、
Bの変換規則を「A」**とします。
変換規則に則り文字Aを変化させると以下のようになります。
第1世代 - A
第2世代 - AB
第3世代 - ABA
第4世代 - ABAAB
第5世代 - ABAABABA
L-Systemのその他の応用例などはこちらから参照してください。
#準備するもの
・L_System_Tree - Actor型
・BranchData - 構造体 - 内容は以下の通り
・Branch_Mesh - Static Mesh
ModesのGeometryからCylinderをマップ上にドラッグ&ドロップ
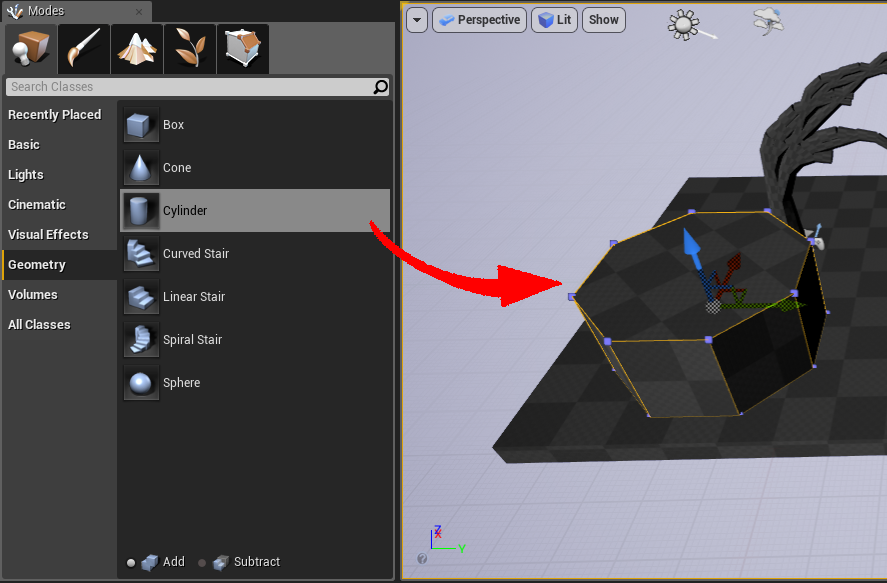
詳細パネルでサイズを**(0.25, 0.25, 1.0)に変更した後に項目Brush Settings内にあるCreate Static Mesh**をクリックしてスタティックメッシュを作成します。
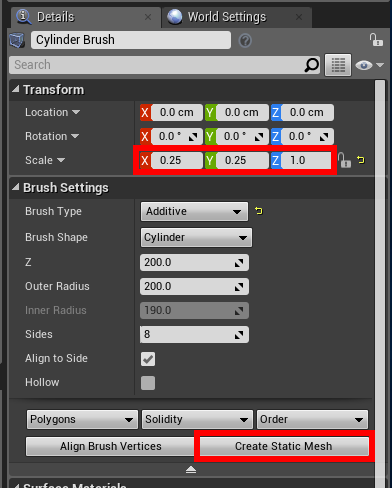
これで必要最低限のものは揃ったので、次はL_System_Treeアクターに変数を追加していきます。
#L_System_Treeアクター
このアクターはL-Systemアルゴリズムを実行する本体です。
使用する変数群は以下のようになります。
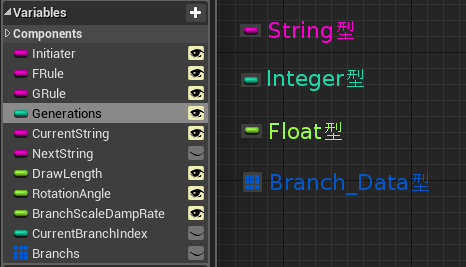
変数BranchsはBranchData型の配列です。（画像の方ではアンダーバーが付いていますが、これは間違いです。）
一通り変数を追加したら、アクタにコンポーネントを追加します。
Turtle - Static Mesh Component
Spline - Spline Component
##関数「Generate LSystem」
L_System_Treeアクターに新しく関数「Generate LSystem」を追加します。
この関数はL-Systemの各変換ルールを文字列に実際に適用する関数です。
世代数分ループをし、初期文字列からどんどん成長させます。L-Systemを実現する最も重要な関数です。
関数を追加したら以下のローカル変数を追加します。
Local Strings - String型（配列）
InputsとOutputsについては何も触る必要はありません。空っぽのままでOKです。
関数の内容は以下の通りです。（画像サイズがかなり大きいです）
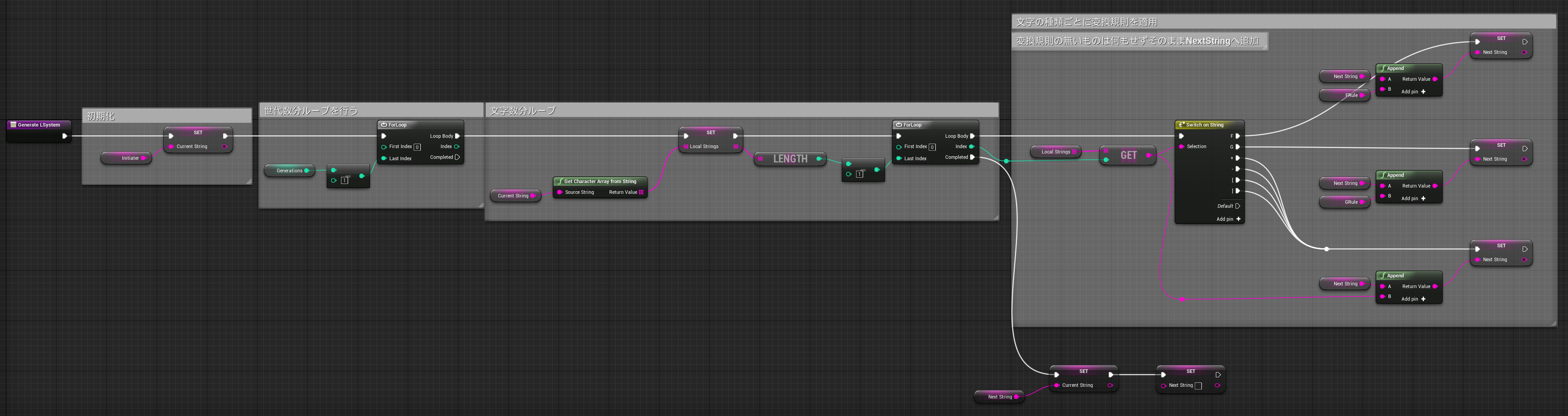
最も重要といいつつも内容はいたって単純だと思います。
最初のループは世代数分のループです。２つめは変数CurrentStringに格納されている文字列を配列として取り出し、要素数分（文字数分）のループを行っています。
Switch文では取り出した文字ごとに処理を分岐させています。
文字Fが来た場合はFの変換ルールを適用し、変数NextString（次世代の文字列）へと格納されます。
Gの場合もFと同様です。
FとG以外の文字は変換ルールはありませんので、取り出した文字をそのまま変数NextStringへ格納しています。
では、処理が書けたらL_System_TreeアクターのConstruction ScriptにGenerate LSystemを呼び出すようにノードを繋げます。
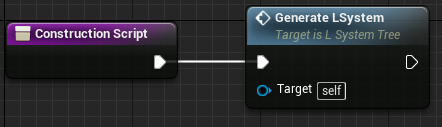
繋げたらL_System_Treeアクターをシーン上に配置します。
そうすると詳細パネルに編集可能な変数が表示されるはずなので、以下のように設定します。
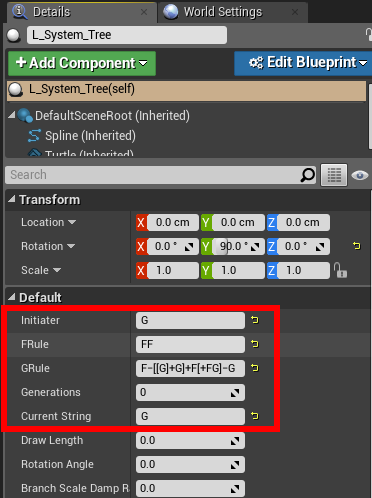
画像の赤で囲まれた項目のように表示されていなかったら、変数の追加の項目まで戻り目のアイコンをONにしてください。
画像のように設定出来たら、Generationsを１ずつ増やしてみてください。
Generations 0 ＝ G
Generations 1 ＝ F−[[G]+G]+F[+FG]−G
Generations 2 ＝ FF[[F−[[G]+G]+F[+FG]−G]+F−[[G]+G]+F[+FG]−G]+FF[+FFF−[[G]+G]+F[+FG]−G]F−[[G]+G]+F[+FG]−G
というようになればOKです。
##関数「Generate Tree」
この関数では準備段階で追加したStatic MeshのTurtleを操作して、タートルグラフィックス的なものを作ります。（タートルグラフィックス)
関数を追加したら、以下のローカル変数を追加します。
InputsとOutputsは空っぽです。
処理内容はこちらです。
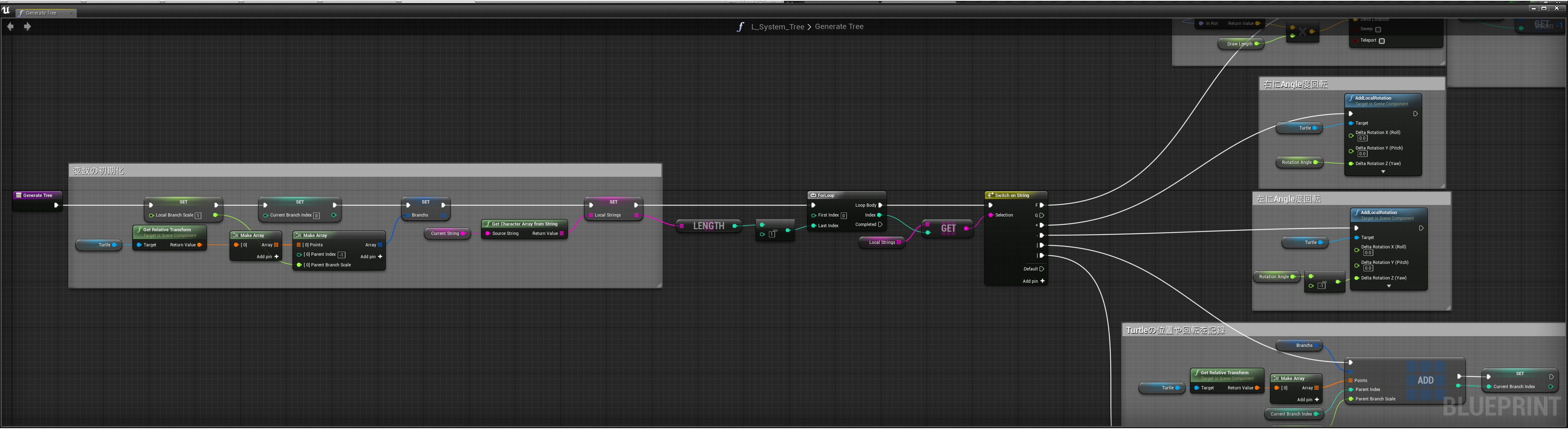
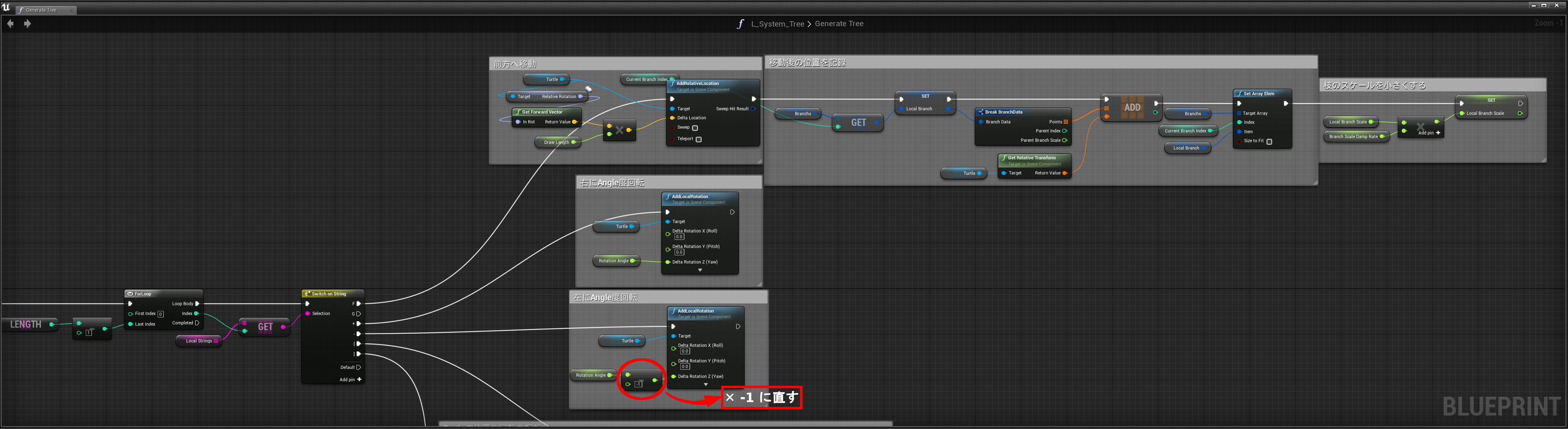
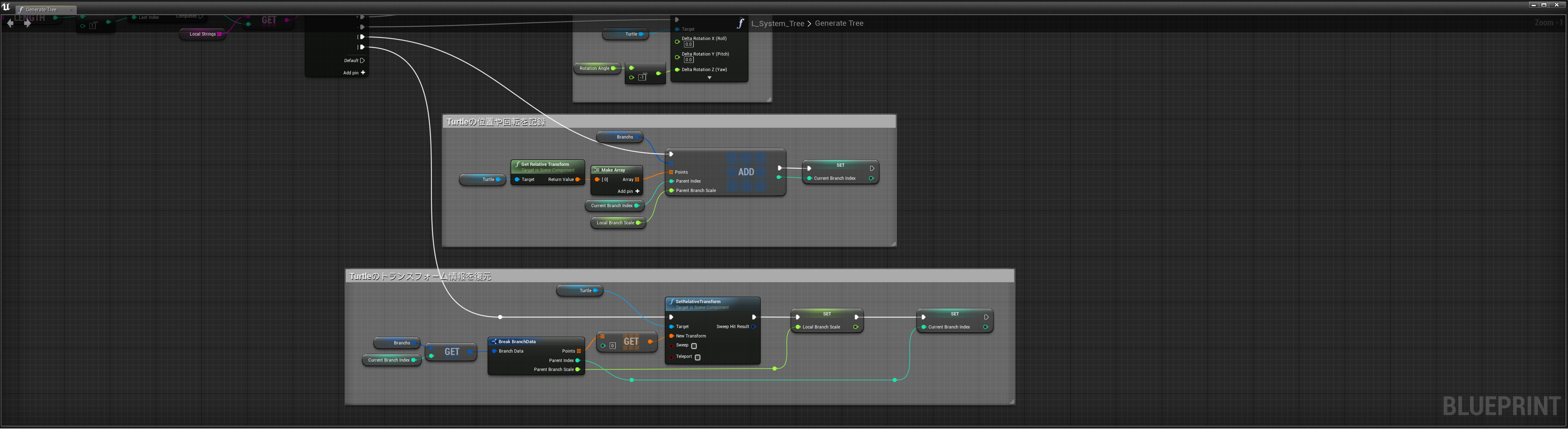
この処理では各文字（F、+、-、[、]）ごとにTurtleに対する操作を記述しています。
F - Turtleを前方に移動し、移動後の位置を記録
+ - Turtleを右にAngle度回転
- - Turtleを左にAngle度回転
[ - Turtleのトランスフォーム情報を記録＆ブランチの作成
] - Turtleのトランスフォーム情報を復元
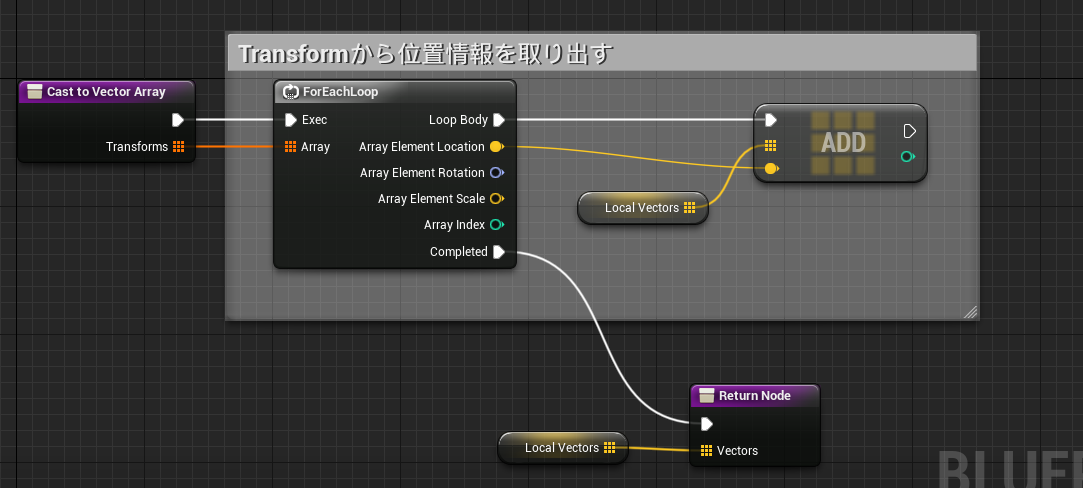
##関数「Cast To Vector Array」
この関数は引数でトランスフォーム情報を受け取り、位置を表すVectorを取り出し、配列に格納し直して返す処理をします。ちょっとした便利関数です。
ローカル変数にVector型の配列を追加します。名前はLocal Vectorsとします。
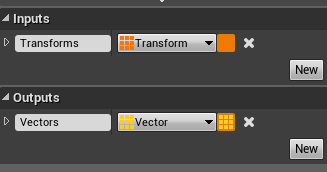
続いてInputsにTransform型の配列を追加。名前をTransformsにします。
OutputsはVector型の配列で名前をVectorsとします。
処理内容は以下の通りです。
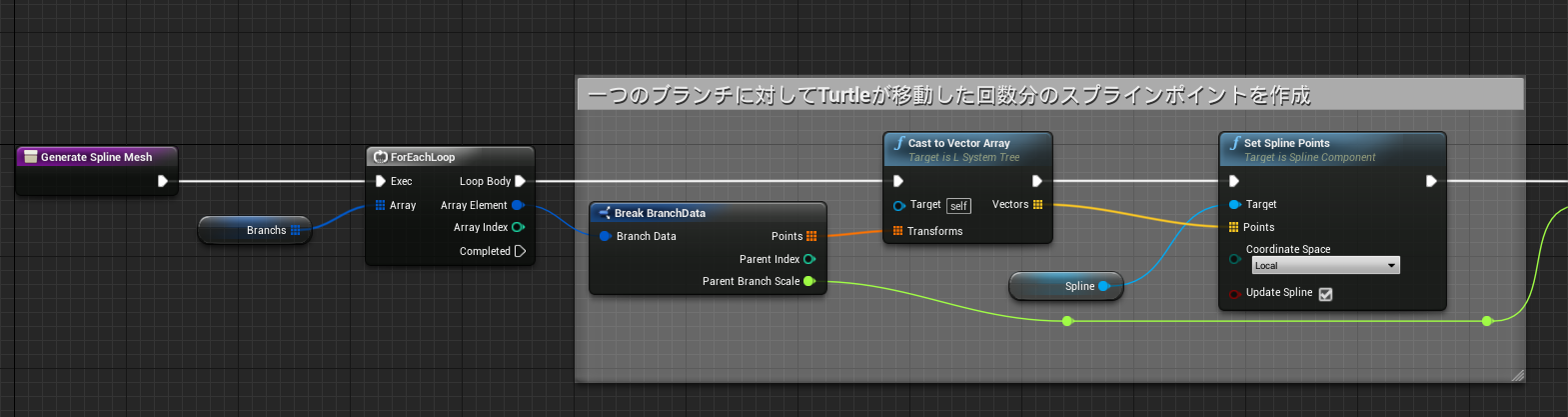
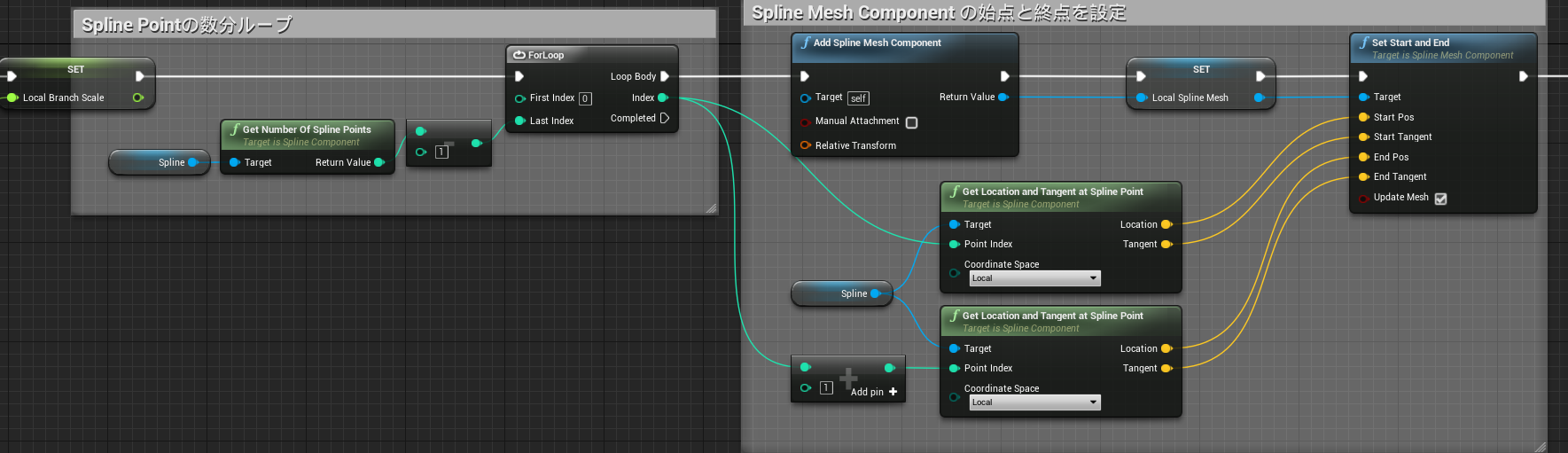
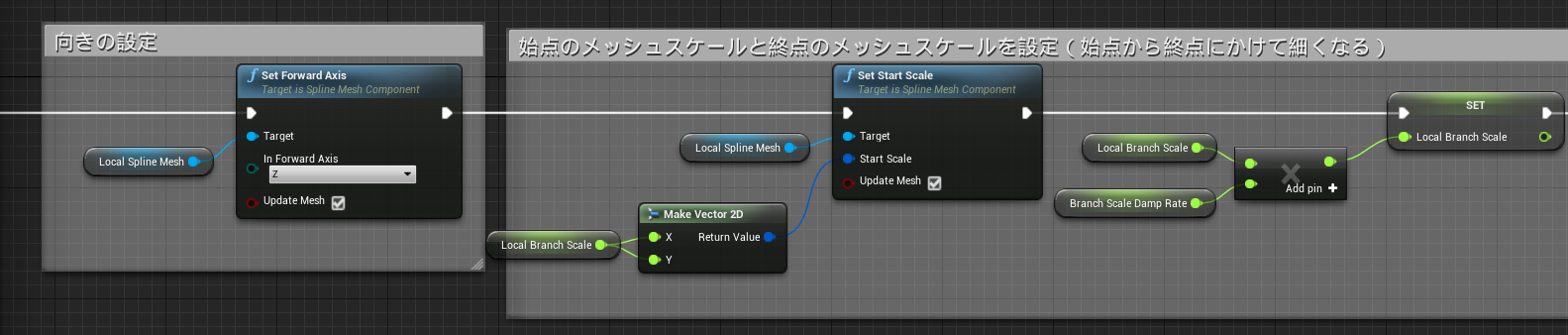
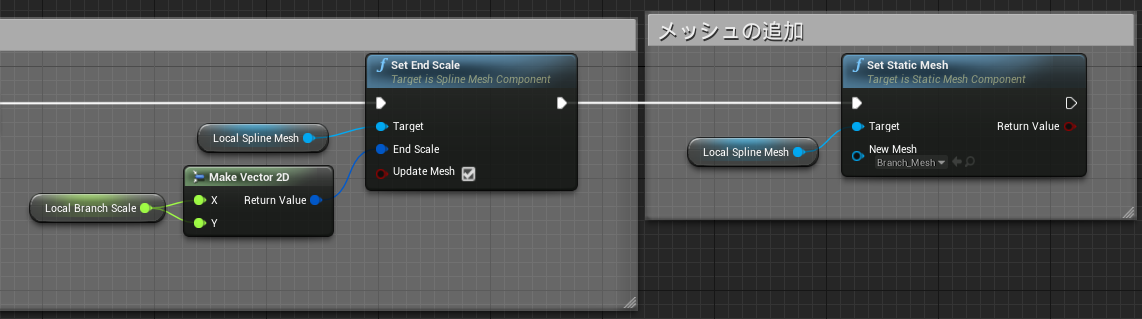
##関数「Generate Spline Mesh」
ここではGenerate Tree関数で記録されたTurtleの位置情報を元にSpline Meshを配置していきます。この関数により今まで文字列でしか表現されていなかったL-Systemを目で見える状態にします。
ローカル変数を追加します。
Float型 - Local Branch Scale
Spline Mesh Component型 - Local Spline Mesh
InputsとOutputsは空っぽでOKです。
処理内容は以下の通りです。
#最終動作確認
以上でL-Systemアルゴリズムを作成し、実際に描画させるところまで出来ました。
では、Construction Scriptに作成した関数を配置します。
無事にコンパイル出来たら、マップ上にL_System_Treeアクターを配置し、詳細パネルで以下のように編集してください。
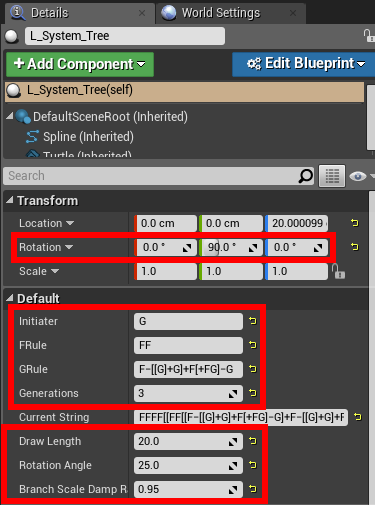
値を設定するとL_System_Treeアクターは以下のように変化するはずです。
あとは、Generationsを増やすと木がどんどん成長していきます。
一つ注意点としてGenerationsの値を極端に増やさないでください。
Generationsを6にしただけでも４，５分ほどUE4がフリーズ、もしくはクラッシュします。（PCの処理性能にもよると思いますが..）
Generationsが6の場合の文字数をカウントしてみると
このようになりました。
L-Systemの作り方は以上です。お疲れ様でした。
#おまけ
##フラクタルツリー
L_System_Treeアクターの各変数を以下のように設定すると
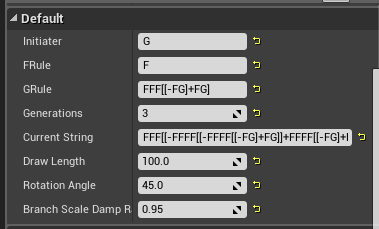
フラクタルツリーと呼ばれる自己相似性を持つ木が生成されます。
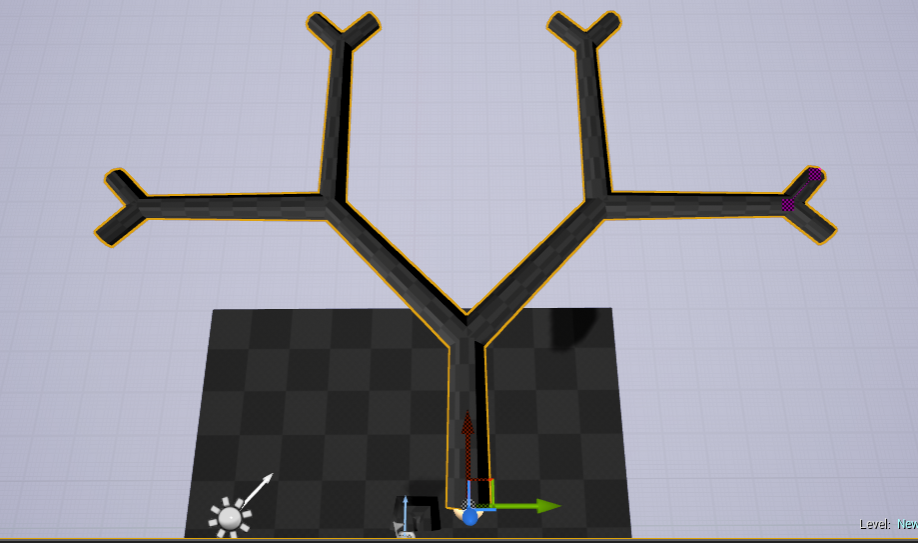
##ランダムな回転度数
関数「Generate Tree」内の回転処理部分にて、以下のように度数をランダムする処理を挟むと
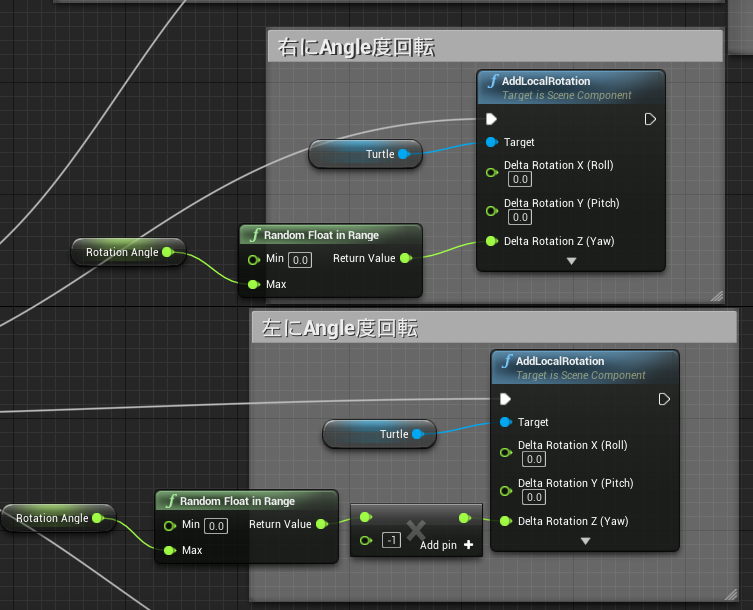
少し現実に近い見た目の木も生成できます。
#編集履歴
2017/02/11 関数Generate Tree内のSwitchのー（マイナス）ピンから繋がるノードの処理を修正