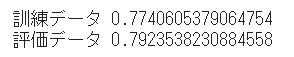言語処理100本ノック2020 (70~74)

はじめに

本記事は言語処理100本ノックの解説です。
100本のノックを全てこなした記録をQiitaに残します。
使用言語はPythonです。

今回は第8章: ニューラルネット(70~74)までの解答例をご紹介します。

第6章で取り組んだニュース記事のカテゴリ分類を題材として，ニューラルネットワークでカテゴリ分類モデルを実装する．なお，この章ではPyTorch, TensorFlow, Chainerなどの機械学習プラットフォームを活用せよ．

70. 単語ベクトルの和による特徴量

コード

from gensim.models import KeyedVectors
import pandas as pd
import re
import torch

def EncoderNN(sign):
    if sign == "b":
        code = 0
    elif sign == "t":
        code = 1
    elif sign == "e":
        code = 2
    elif sign == "m":
        code = 3
    else:
        print("Error")
    return code

def Text2Vec(text):
    lines = text.split(" ")
    vec_sum = 0
    length = 0
    for line in lines:
        try:
            temp = model.get_vector(line)
            vec_sum += temp
            length += 1
        except:
            pass
    return vec_sum/length

def TorchData(data):
    df = pd.read_table("[PATH]/{}.txt".format(data))
    sign_regrex = re.compile('[!"#$%&\'()*+,-./:;<=>?@[\\]^_`|＄＃＠£â€™]')
    f_regrex = lambda x:sign_regrex.sub("", x)
    df["TITLE"] = df["TITLE"].map(f_regrex)
    X_torch = torch.tensor(df["TITLE"].apply(Text2Vec))
    torch.save(X_torch, "[PATH]/X_{}.pt".format(data))
    df["CATEGORY"] = df["CATEGORY"].map(EncoderNN)
    Y_torch = torch.tensor(df["CATEGORY"])
    torch.save(Y_torch, "[PATH]/Y_{}.pt".format(data))

model = KeyedVectors.load_word2vec_format("[PATH]/GoogleNews-vectors-negative300.bin", binary=True)
TorchData("train")
TorchData("test")
TorchData("valid")

コメント
Pytorchで学習できる型で保存。機械学習はデータの型で苦労する場合もあると思います。

71. 単層ニューラルネットワークによる予測

コード

import torch.nn as nn
import torch

class NetWork(nn.Module):

    def __init__(self, input_feature, output):
        super().__init__()
        self.fc1 = nn.Linear(input_feature, output, bias=False)
        nn.init.xavier_normal_(self.fc1.weight)#重みをXavierの初期化
        self.fc2 = nn.Softmax(dim=1)

    def forward(self, x):
        x = self.fc1(x)
        x = self.fc2(x)
        return x

X_train = torch.load("[PATH]/X_train.pt")
model = NetWork(300, 4)
model(X_train)

出力結果

コメント
4カテゴリに対して、それぞれ確率を表しています。学習を一切していないので大体0.25あたりですね。

72. 損失と勾配の計算

コード

import torch
import torch.nn as nn
#############71################
class NetWork(nn.Module):
    def __init__(self, input_feature, output):
        super().__init__()
        self.fc1 = nn.Linear(input_feature, output, bias=False)
        nn.init.xavier_normal_(self.fc1.weight)#重みをXavierの初期化
        self.fc2 = nn.Softmax(dim=1)
    def forward(self, x):
        x = self.fc1(x)
        x = self.fc2(x)
        return x
        
X_train = torch.load("[PATH]/X_train.pt")
model = NetWork(300, 4)
################################

loss = nn.CrossEntropyLoss(reduction="mean")
Y_train = torch.load("[PATH]/Y_train.pt")
Y_pred = model(X_train)
CEloss = loss(Y_pred, Y_train)

model.zero_grad()
CEloss.backward()
print("クロスエントロピー損失", CEloss.item())
print("勾配", model.fc1.weight.grad)

出力結果

コメント
CEloss.backward()で誤差逆伝搬の計算をしてます。ニューラルネットワークのように多層になっても重みを更新できるのはこのロジックのおかげです。

73. 確率的勾配降下法による学習

コード

from torch.utils.data import TensorDataset, DataLoader
import torch
import torch.nn as nn
import torch.optim as optim
#############71################
class NetWork(nn.Module):

    def __init__(self, input_feature, output):
        super().__init__()
        self.fc1 = nn.Linear(input_feature, output, bias=False)
        nn.init.xavier_normal_(self.fc1.weight)#重みをXavierの初期化
        self.fc2 = nn.Softmax(dim=1)

    def forward(self, x):
        x = self.fc1(x)
        x = self.fc2(x)
        return x

X_train = torch.load("[PATH]/X_train.pt")
model = NetWork(300, 4)
################################
loss = nn.CrossEntropyLoss(reduction="mean")
Y_train = torch.load("[PATH]/Y_train.pt")

ds = TensorDataset(X_train, Y_train)
DL = DataLoader(ds, batch_size=128, shuffle=True)
optimizer = optim.SGD(params=model.parameters(), lr=0.01)

epoch = 100
for ep in range(epoch):
    for X, Y in DL:
        Y_pred = model(X)
        CEloss = loss(Y_pred, Y)
        optimizer.zero_grad()
        CEloss.backward()
        optimizer.step()

torch.save(model.state_dict(), "[PATH]/SigleLayer.pth")#モデルの保存

コメント
情報系研究生へ、学習後のモデルは保存しましょう。

74. 正解率の計測

コード

import torch
import torch.nn as nn
#############71################
class NetWork(nn.Module):
    def __init__(self, input_feature, output):
        super().__init__()
        self.fc1 = nn.Linear(input_feature, output, bias=False)
        nn.init.xavier_normal_(self.fc1.weight)#重みをXavierの初期化
        self.fc2 = nn.Softmax(dim=1)
    def forward(self, x):
        x = self.fc1(x)
        x = self.fc2(x)
        return x

model = NetWork(300, 4)
################################
model.load_state_dict(torch.load("[PATH]/SigleLayer.pth"))
X_test = torch.load("[PATH]/X_test.pt")
Y_test = torch.load("[PATH]/Y_test.pt")
X_train = torch.load("[PATH]/X_train.pt")
Y_train = torch.load("[PATH]/Y_train.pt")

Y_pred = model(X_train)
result = torch.max(Y_pred.data, dim=1).indices
print("訓練データ", result.eq(Y_train).sum().numpy()/len(Y_pred))
Y_pred = model(X_test)
result = torch.max(Y_pred.data, dim=1).indices
print("評価データ", result.eq(Y_test).sum().numpy()/len(Y_pred))

出力結果

コメント
評価データの方が精度高い。。。
もっと過学習ぎみにチューニングした方が良かったかな。

後半の解答

他章の解答例