E問題をトポロジカルソートっぽく解いた話
公式解説のYoutube放送中にコメントで「トポロジカルソートで解いた」と書いたらsnukeさんに「どうやって解くんだろ」と言われたので「あれ?あまり一般的な解法ではないのかな」と思ってここで共有させていただきます。Qiitaに解法記事を載せるのは初めてなので、図や文章が読みづらかったらゴメンナサイ。
問題を見たときまず考えたこと
ABC256Eこれ見た瞬間に、まず真っ先に頭に浮かんできたのはABC223Dだったんですよね。こういう「AさんはBさんより先に」みたいな問題構造はA→Bの有向グラフだと捉えると上手くいくケースが多いです。
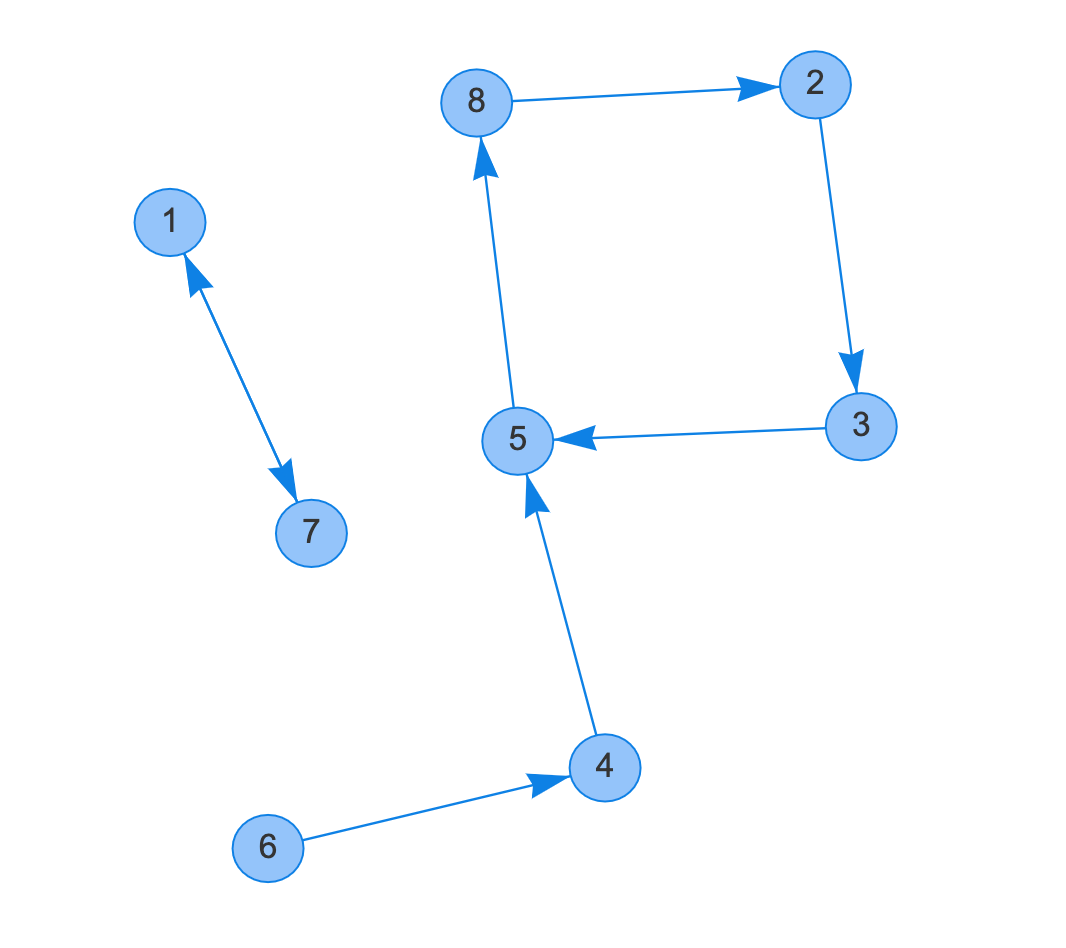
実際に今回の問題の入力例2を元にすると、こんな感じの有向グラフが出来上がります。
具体的にどう解いたか
トポロジカルソートの説明自体は他に優良な記事がいくらでもあると思うので割愛します。上の図で考えると6は入次数が0なので不満度0でキャンディを配ることが出来ます。6にキャンディを配ると次は4の入次数が0になるので4も不満度0でキャンディを配ることが出来ます。ただのトポロジカルソートであればここで終了です。トポロジカルソートの結果がlen([6,4])!=nなので「このグラフはDAGじゃないね」でオワリ。
そうすると残ったのは[1,7]と[2,3,5,8]の有向閉路グラフが残ります。この有向閉路グラフは「誰かに先にキャンディを配ると必ず誰かが不満になる」ということなので、どうせ不満が貯まるならこの閉路のメンバーの中で最も不満度が低い人に不満になってもらおう、そういう方針でコーディングしたらACでした。この「閉路メンバーの中で最も不満度が低い人」を取り出すために、私は優先度付きキューを使用しました。以下が、実際にコンテスト中に提出したコードになります。(コメントを追加しています)
import heapq
n=int(input())
x=list(map(int,input().split()))
c=list(map(int,input().split()))
in_deg=[0]*n#indegree=入次数のこと
g=[[] for _ in range(n)]
for i in range(n):#0_index派です
g[i].append(x[i]-1)
in_deg[x[i]-1]+=1
q=[]
for i in range(n):
if in_deg[i]==0:
heapq.heappush(q,(0,c[i],i))#入次数0なら頭に0をつけておく
else:
heapq.heappush(q,(1,c[i],i))#入次数>0なら頭に1をつけておく
visit=[False]*n
ans=0
while q:
ind,point,now=heapq.heappop(q)#入次数0のものから取り出せる。次に不満度が低い順に取り出せる。
if visit[now]:
continue
visit[now]=True
if ind==0:#入次数が0なら不満度は0
for to in g[now]:
if visit[to]:
continue
in_deg[to]-=1
if in_deg[to]==0:#新たに入次数0の頂点が出現したらキューに入れる
heapq.heappush(q,(0,c[to],to))
else:#入次数>0なら不満が貯まる
ans+=point
for to in g[now]:
if visit[to]:
continue
in_deg[to]-=1
if in_deg[to]==0:#新たに入次数0の頂点が出現したらキューに入れる
heapq.heappush(q,(0,c[to],to))
print(ans)
Pypyで1600ms程度だったのでまず問題ない速さだと言えるでしょう。
余談
提出した後に「これってSCC(強連結成分分解)でも解けるやん」と気付きました。SCCのライブラリ貼っつけて提出したらPypyで300msだったのでこっちのほうが圧倒的に速いですね。また解説放送や公式解説に出て来ましたがUnionFindを使う方法など、もっと効率的なアルゴリズムがたくさんありましたね。