はじめに
情報系の学科でCSを学習している学部2年のDot-P (@DotP_engineer) です![]()
今回は、タブー探索(タブーサーチ)というメタヒューリスティック手法をスタイナー木問題を通して解説していこうと思います。
この記事は局所探索法についてある程度知識がある方向けに書いた記事になります。
他のメタヒューリスティック解法である焼きなまし法や遺伝的アルゴリズム、ビームサーチ等については解説を行っていませんのでご注意ください![]()
スタイナー木問題について知らなくてもある程度は理解できるようにしてあるので是非一読していただければなと思います。
タブーサーチの概念から実装まで一通り説明するので最後まで読んでいただければ幸いです。
自己紹介
工学部の情報系学科2年。 C++とLinuxが好きです![]()
深層学習を学習しようと思ったのですが、ただただチューニングするだけではあまり面白みがないと感じ、ヒューリスティック解法も現在勉強中です。
タブー探索法を使おうとした際、ほとんどの資料が英語でしたので、今後学習される方がより簡単にタブー探索法を理解できるようにこの記事を書いています
国語は苦手なため、読みづらい文章かもしれませんが、誰か1人のためにでもなれば幸いです![]()
SNS
・Twitter: @DotP_engineer (←モチベーションの増加になるので、フォローしてね)
・Qiita: https://qiita.com/DotP_engineer
・Github: https://github.com/Dot-P
・Atcoder: https://atcoder.jp/users/Dot_P (今年の2月から始めました!)
スタイナー木問題とは?
そもそもスタイナー木問題とは何でしょうか?
場合によってはシュタイナー木問題とも表現されます。英語表記だと「Steiner Tree」です。
Wikipediaではスタイナー木を以下の通りに定義しています。
シュタイナー木(Steiner tree)とは、辺の集合Eと頂点の集合Vから成る無向グラフG=(V,E)と、ターミナルと呼ばれるVの部分集合Tが与えられたとき、Tの全ての頂点を連結する木のことである。[Wikipediaより引用]
つまり、スタイナー木問題とは、Vという頂点の部分集合が与えられたとき、Vに含まれる任意の頂点を含むグラフの重さを最小にする問題である。
これだけではわかりずらいと思うので具体例を考えます。
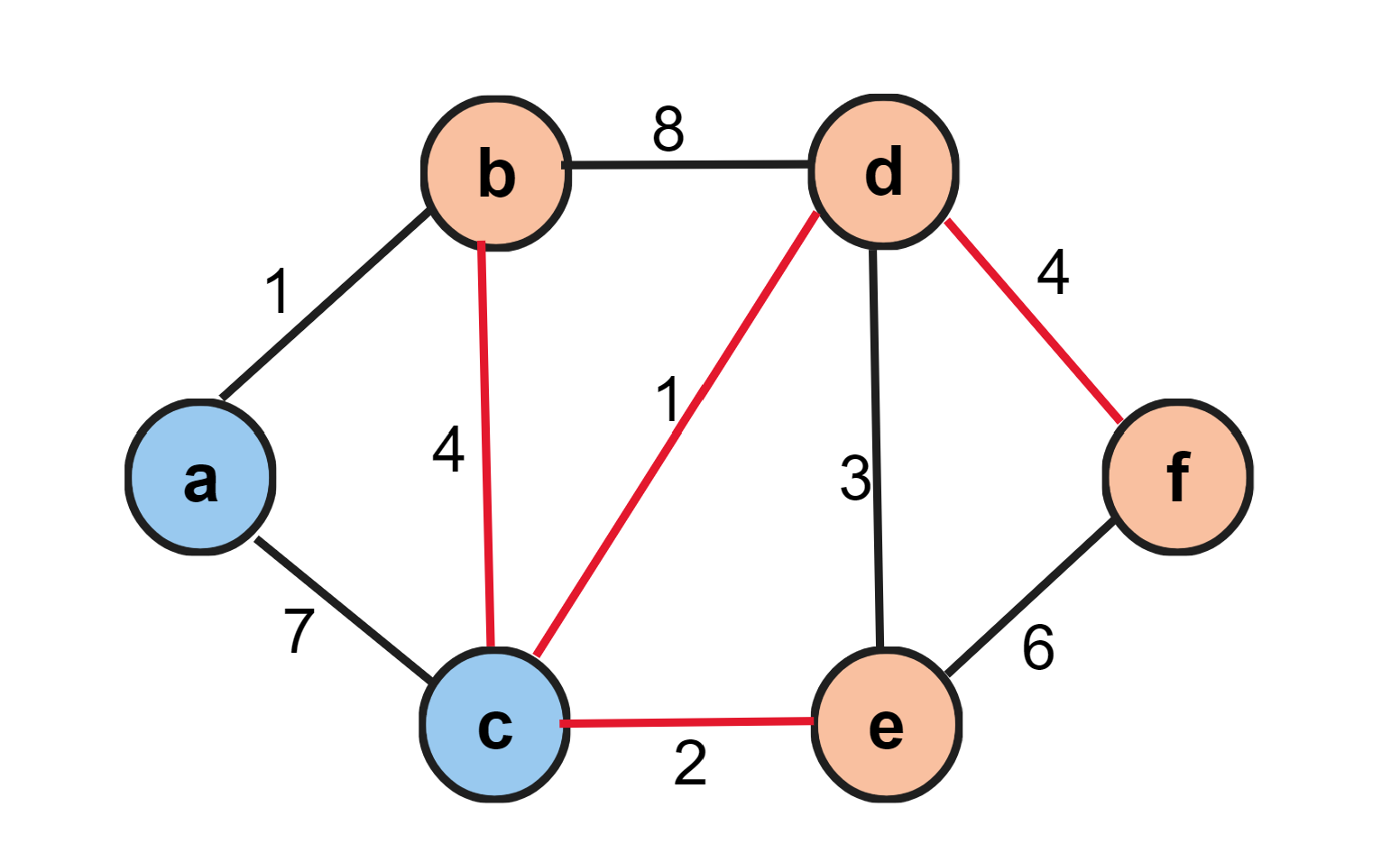
上図のようなグラフGを与えられたと仮定します。グラフGは、a, b, c, d, e, fの6つの頂点と、9つの辺で構成されています。辺の近くにある数字は重みを表しており、例えばa-b間の重みは1です。Vはオレンジの頂点とし、上図の場合、V={b, d, e, f}です。
つまり、スタイナー木問題とはオレンジ色の頂点を必ず含むように注意しながら重さが最小の木を求める問題です。今回の場合は以下の場合が最適解です。
重さは11が最小となります。ここで、Vの頂点集合に含まれない頂点cが最小木として含まれていますが問題ありません。あくまでも、スタイナー木問題はVの頂点集合を含んでさえいればいいです。今回のようにb, d, e, fを直接つなぐグラフよりも一瞬迂回しているように思える木のほうが最小の重さを持つことは全然ありえます。
今回挙げた例は非常に頂点や辺の数が少ないので少し考えれば最小であることが確認できますし、全探索してもそれほど大きな計算量になりません。
しかし、頂点数や辺の数が大きいケースを考えてみましょう。頭がおかしくなりそうですよね。計算量がとんでもなく大きくなってしますので、全探索しているうちにおそらく一生を終えてしまいます。
スタイナー木問題はNP困難であるといわれており、値が大きい場合、最適解を求めることが難しくなります。
そこで最適解にできるだけ近い近似解を許される時間の範囲内で求めてあげます。局所探索法は近似解を求めるのに適しており、局所的に優れた解を求めることができます。しかし、ここで問題が起こります。一般的な局所探索法はマクロな視点を持っていませんので、局所最適解のドツボにはまります。
例えば上の画像をスコアを可視化したものとしましょう。初期解がCであるとします。すると、局所探索法では自分の周囲よりもスコアが良くなるようであれば遷移するのでCからBの方向へ徐々に近づいていきます。しかし、Bに到達した後はTに向かうことができません。なぜなら、Bの周囲はBよりも低いスコアで遷移できないからです。上の図は明らかにTが最適解ですのでTにどうしても近づきたいものです。そこで登場するのがタブー探索法です。次のセクションでタブー探索法について解説します。
タブー探索法とは?
タブー探索法は以下のように定義されています。
この手法は状態の近傍を複数探索しその中で最も良い近傍状態に遷移する、このときタブーリストと呼ばれるキューに状態遷移時の操作を書き込む。このタブーリストに書き込まれている操作は行わないことにより状態がループするのを防ぐことで探索が停滞せずに最適解を探索する。(Wikipediaより引用)
簡単に言うと以下の通りです。
タブー探索法
最近探索した解を「タブーリスト」に記録し、それらの解に再度到達しないようにすることで局所最適解からの脱出を図る。
ずばり、タブー探索法は禁じ手を決めます。例えば同じようなことを繰り返えすことを防ぐことができます。その際に禁じ手を保存するタブーリストを用意します。タブーリストに何を保存しておくか、どのくらいのサイズにするのかは皆さん次第です。勿論、それらはスコアにも影響してきます。ちなみに今回私が用意したスタイナー木問題の解法ではどの頂点を加えたか、削除したかの情報をサイズ7のタブーリストに保存しています(のちに詳しく説明します) 。
タブー探索の場合、概念としては以下のようになります。
1. 初期解 U0 の作成
2. 各変数の初期化
3. 近傍のすべての U を調べて最良スコアをもつ U' と今のベストスコア Ub と比較
4-1. もし、スコアを更新していれば、タブーリストを更新し探索を続ける。(3へ戻る)
4-2. そうでなければ、タブーリストを確認。もし、禁じ手であればランダムな解を作成するなどし脱却を図る。(2へ戻る) 禁じ手でなければ、タブーリストを更新して探索を続ける。 (3へ戻る)
5. 実行時間を過ぎたらベストスコア Ub を出力。
4番に関しては複雑なので図解しようと思います。
では実際に見ていきましょう。まずスコアが改善されているかを確認します。もしスコアが改善していたらアスピレーションクライテリオンを行います。アスピレーションクライテリオンとは以下のようなものです。
アスピレーションクライテリオン(Aspiration Criterion)
特定の条件下でタブーリストの制約を緩和するためのルール
例えば、「スコア改善があったとき」というのが特別な条件下にあたります。近傍を探索した最良のコストがこれまでのベストスコアよりも良ければ、今行った探索がタブーであったとしても例外として採択し探索を継続するということです。
よくよく考えてみれば当たり前っちゃあ当たり前です。スコアが伸びてるのに禁じ手だからと打ち切りにするのはもったいないと思いませんか? スコアが伸びているのなら続けても構わないと思うのが普通でしょう。このような動作を取り入れたのがアスピレーションクライテリオンの良さです。タブーリストに関しては、先頭に行った操作を持ってきて全体を移動させます。(先頭にもってくることは一番最近の操作として履歴を残しておくということです)
なぜ移動させたか分からない人はタブーリストの役割を以下のように覚えるとよいです。
タブーリスト
スコア改善が起こらなかった場合に直近数回分と同じ操作をすることを禁じるためのメモである。
アスピレーションクライテリオンの場合、例外的に操作を受け入れるのでタブーリストに同じ操作の情報が含まれています。そのため、その操作を一番新しく行った操作として先頭に持ってきます。そうすることで以後探索しても一定期間タブー操作として残ることになります。
次にスコア改善しなかった場合を考えましょう。この場合は行った探索がタブーかどうかを考えなくてはなりません。
もし、タブーでなければ探索を続けます。これは一時的にスコアが伸びなかった可能性を考慮したうえでの動作です。そもそも、タブーでないなら無限ループに陥っている可能性はかなり低いです。そのため、今後のスコアの伸びを期待して探索を継続させます。このとき、タブーリストの先頭に今行った操作の情報を記載し、最も古い情報を破棄します。
もし、タブーであった場合、残念ながら局所最適解のドツボにはまっている可能性が高いです。そのため、スタート地点を変更してもう一度やり直します。(最良解は勿論、保存しておきます)この際の解の生成は毎回同じでなければなんでも構わないです。これをランダムリスタートといいます。
ランダムリスタート(Random Restart)
解空間内の任意の位置から探索を開始する手法
乱数を生成し、それに基づいて新たな解を作成するのが一番簡単な方法であると思います。しかし、実行時間が短い場合ではうまく初期解を作り直さなくてはならなく、これがコンテストの順位決めに影響する要素になりえます。はじめは簡単な実装を作ってから複雑で効率的なコードを書くとよいでしょう。
これでタブー探索法の本質については説明し終わりました。次のセクションでは実際にスタイナー木問題を解きながらタブー探索の理解を深めていこうと思います。
スタイナー木問題におけるタブー探索
まず初めに実装コードの解説を行います。量が多いため、主要な箇所のみを解説します。
最後に全体のコードも書いておいたのでよかったら見て行ってください!
/*ダイクストラ法による最短距離と最短経路の作成*/
for(i=0; i<K; i++){
dijkstra(S[i], N, M, edge, d[i], p[i]);
}
/*グラフG_auxの作成*/
k = 0;
for(i=0; i<K; i++){ //K個の頂点からなるグラフの辺の数はK(K-1)/2
for(j=0; j<i; j++){
G_aux[k].end2 = i;
G_aux[k].end1 = j;
G_aux[k].weight = d[i][S[j]];
k++;
}
}
/*クラスカル法による最小木の探索*/
for(i=0; i<M; i++){
ednum[i] = i;
T[i] = 0;
}
Kruskal(K, k, G_aux, ednum, T);
/*最小木に含まれる頂点を全てUに追加*/
for(i = 0; i<K*(K-1)/2; i++){ //各頂点が最小木に含まれればU0_checkに1を代入
if(T[i] == 1){
u = G_aux[i].end1;
v = S[G_aux[i].end2];
U0[S[u]] = 1;
//printf("%d!\n",S[u]);
U0[v] = 1;
//printf("%d!\n",v);
while(p[u][v] != S[u] && p[u][v] != v){
U0[p[u][v]] = 1;
//printf("%d!\n", p[u][v]);
v = p[u][v];
}
}
}
初期解を作成するうえで行っていることは以下の4点です。
①Sの各頂点をスタート地点としたDikstra法を実行し、最短距離Dと最短路Pを取得
↓
②Sの頂点から選んだ任意の2つの頂点をG_auxの頂点、その最短距離をG_auxの重みとする
↓
③グラフG_auxに対してkruskal法を実行し最小木を作成
↓
④最短路Pを参照し、最小木に含まれる頂点をインデクスとしたUに1を代入
change=neighborhood(edge,ednum,U,Umin,Is,N,M,&score,T);
/*以下、一部省略*/
int neighborhood(struct edge_data *edge, int *ednum,int *U, int *Umin, int *Is, int N,int M, int *score,int *T){
int Iutemp[maxN];
int Iutemp2[maxN];
int i,j,x,y,z,k;
int change;
y=inf;
k=0;
for(i=0;i<N;i++){
Iutemp2[i]=0;
}
for(i=0; i<N; i++){
if(Is[i]==0){
for(j=0; j<N; j++){
Iutemp[j]=U[j];
}
if(U[i]==0){
Iutemp[i]=1;
change=i;
}else{
Iutemp[i]=0;
if(i==0){
change=300;
}else{
change=-i;
}
}
x=function(N, M, edge, ednum, Iutemp,T);
Iutemp2[i]=x;
if(x<y){
for(j=0; j<N; j++){
y=x;
Umin[j]=Iutemp[j];
k=change;
}
}
}
}
*score=y;
return k;
}
近傍探索はBest move、つまり近傍探索をして優れたものがあればすぐそれに遷移するのではなく、探索可能な近傍のスコアをすべて出してから最も優れたスコアを持つ近傍の操作を受け入れるということを行っています。そのため、以下のような手順でコードを書いています。
①頂点がSに含まれていないとき、頂点を追加、もしくは削除
↓
②F(U')を計算し、スコアを最小にする頂点集合を配列Uminとし、スコアを変数scoreに代入
↓
③削除した頂点はマイナス、追加した頂点はプラスを使って表現したものを戻り値とする
③については後に詳しく解説します。
if(score <= high_score){
for(i=0; i<N; i++){
Ub[i] = Umin[i];
U[i] = Umin[i];
}
high_score = score;
if(high_score < best_score){
best_score = high_score;
printf("current_score = %d\n", best_score);
}
if(check_taboo(taboo, change)){ //もし、変更箇所が禁じ手であったら
/*ここが機能してことが一度もない*/
printf("taboo!\n");
//その部分をタブーリストの一番新しい記録に移動する
for(i=t_list_size-1; i>=0; i--){
if(taboo[i] == change){
for(j=i; j>=1; j--){
taboo[j] = taboo[j-1];
}
taboo[0] = change;
}
}
}
}
else{
if(check_taboo(taboo, change)){ //もし、変更箇所が禁じ手であったら
// 新しい初期解 U を求めるためにランダムリスタートする。
random_restart(N, S, K, U);
//initial_solution(edge, N, M, K, *d, *p, S, U);
high_score = function( N, M, edge, ednum, U, T);
//タブーリストの初期化
for(i=0; i<t_list_size; i++){
taboo[i] = inf;
}
}
else{
for(i=0; i<N; i++){
U[i] = Umin[i];
}
//changeをタブーに入れる(全体を移動する)
//溢れた場合は、一番古い記憶を削除する
for(i=t_list_size-1; i>=1 ; i--){
taboo[i] = taboo[i-1];
}
taboo[0] = change;
}
}
まず初めにタブーリストの作り方を説明します。
今回上記のものをタブーリストとして定義しています。頂点を追加した際は正、削除した場合は負の数で表現します。しかし、頂点0をこのままでは表現することができないので、頂点0を削除した場合は300とすることにしました。これは頂点数が最大でも150個である(今回入力するファイルでは)ので300という数字にはなりえないことが前提としてあります。
そのため、例えば頂点5を削除した場合は-5と表現され、頂点6を加えたときは6と表現されます。
はじめに、INFという大きな値でタブーリストを初期化します。スコア改善が行われなかった場合でタブーでないときはタブーリストの先頭にchangeを挿入します。普通はqueueで実行しますが、今回はどんな言語でも扱えるようにあえて配列で作ってあります。そして一番古い情報を削除します。
もし、画像のような状態にタブーリストがあり、変更changeが-3であったとき、-3をリストの先頭に入れ、それ以降の文字を1つずつ後ろに下げていきます。最後尾であったINFは削除されます。
アスピレーションクライテリオンの場合は、その操作を先頭に持ってきて辻褄があうように配列の移動を行います。
例えば、画像のような状態にタブーリストがあり、変更changeが6であったとき、1、-5、300は一つ後ろに下がり、6は先頭に来ます。そのほかの要素は移動しません。
参考文献
まとめ
いかがでしたでしょうか。タブー探索法やスタイナー木問題について理解できましたでしょうか?
私は初めて解いたとき、あまりの難しさに数時間うなっていました。
この記事を読んだ皆さんがタブー探索法を理解し、フューリスティック解法に興味を持っていただけると嬉しいです![]()
最後に全体のコードを記載して終わりにしようと思います。
コード
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>
#include <time.h>
#define maxN 150
#define maxM 1000
#define inf 10000
#define NIL -1
#define time_limit 0.827904 /* 制限時間 */
#define t_list_size 7 /* タブー化する頂点の数 */
struct edge_data{
int end1; int end2; int weight;
};
/*ダイクストラ法用の構造体*/
struct cell{
int key; int vertex;
};
/* ソート関連の関数 */
void quicksort(int *A, int *ednum, int p, int r);
int partition(int *A, int *ednum, int p, int r);
/* ユニオン・ファインド森の関数 */
void make_set(int *p, int *rank, int x);
int find_set(int *p, int x);
void link(int *p, int *rank, int x, int y);
int set_union(int *p, int *rank, int x, int y);
/* f(U) を求める関数 */
int function(int N, int M, struct edge_data *edge, int *ednum, int *IU, int *T);
int neighborhood(struct edge_data *edge, int *ednum,int *U, int *Umin, int *Is, int N,int M, int *score, int *T);
/*クラスカル法による最小木を求める関数*/
void Kruskal(int N, int M, struct edge_data *edge, int *ednum, int *T);
/*2分ヒープ関連の関数*/
int parent(int i);
int right(int i);
int left(int i);
void Downheap_Sort(struct cell *H, int i, int *adr);
void Insert(struct cell *H, int i, int a, int v, int *adr);
void Upheap_Sort(struct cell *H, int i, int *adr);
void decrease_key(struct cell *H, int i, int a, int *adr);
int Delete_min(struct cell *H, int i, int *adr);
void dijkstra(int v0, int N, int M, struct edge_data *edge, int *d, int *p);
/* ランダムリスタート関連の関数 */
void random_restart(int N, int *S, int K, int *U);
/* タブー関連の関数 */
int check_taboo(int *taboo, int change);
int main(void)
{
int N, M, K; /* N = 頂点数, M = 辺数 , K = ターミナル数(S の頂点数) */
int S[maxN]; /* S = ターミナル集合 */
struct edge_data edge[maxM];
struct edge_data G_aux[maxM]; /*Sに含まれる頂点のグラフ*/
int i,j,k; /* カウンタ */
int u, v; /* 辺 (u, v) */
int d[maxN][maxN], p[maxN][maxN]; /* d[i] = 頂点 i への最短距離, p[i] = 頂点 i の親 */
int ednum[maxM]; /* 昇順における辺の番号 */
int T[maxM]; /* 最小木を表す配列, T[i] = 1 ⇔ 最小木は辺 i を含む */
int U0[maxN]; /* U0 = 初期解を格納する集合 */
//int U0_check[maxN]; /* U0 の要素が 1 であれば U を初期解に含み、 0 であれば初期解を含まない */
int Ub[maxN]; /* Ub = 最適解を格納する集合 */
int Umin[maxN]; /* Umin = f(U)の値が最も小さいものの頂点集合を格納する集合 */
int U[maxN]; /* U = 現在の解を格納する集合 */
int Is[maxN];/*近傍作成に利用する。*/
int best_score=inf; /* 最適解のスコア */
int score=inf; /* 現在の解のスコア */
int high_score=inf; /* 現在探索しているグラフの最適解のスコア */
int taboo[t_list_size]; /* タブー化された頂点を格納する集合 */
int change; /* U'を選ぶ時に追加または削除する頂点。追加の場合は正、削除の場合は負。例外的に0の削除は300 */
char fname[128];
FILE *fp;
clock_t start_t, end_t; /* 時間計測用*/
double utime;
/* ファイルを開いて入力を読み込む */
printf("input filename:");
fgets(fname, sizeof(fname), stdin);
fname[strlen(fname)-1] = '\0';
fflush(stdin);
fp = fopen(fname, "r");
fscanf(fp, "%d %d", &N, &M);
for(i=0; i<=M-1; i++){
fscanf(fp, " %d %d %d", &edge[i].end1, &edge[i].end2, &edge[i].weight);
}
fscanf(fp, "%d", &K);
for(i=0; i<=K-1; i++){
fscanf(fp, " %d", &S[i]);
Is[S[i]]=1;/*Sに入っている頂点を格納する変数。1なら入っていて、0なら入っていない。 近傍作成に使う*/
}
fclose(fp);
/*U0の初期化*/
for(i=0; i<N; i++){
U0[i] = 0;
}
start_t = clock(); /* 時間計測開始 */
/* 辺を重み昇順にソート */
/* ①初期解を発生 */
/*ダイクストラ法による最短距離と最短経路の作成*/
for(i=0; i<K; i++){
dijkstra(S[i], N, M, edge, d[i], p[i]);
}
/*グラフG_auxの作成*/
k = 0;
for(i=0; i<K; i++){ //K個の頂点からなるグラフの辺の数はK(K-1)/2
for(j=0; j<i; j++){
G_aux[k].end2 = i;
G_aux[k].end1 = j;
G_aux[k].weight = d[i][S[j]];
k++;
}
}
/*クラスカル法による最小木の探索*/
for(i=0; i<M; i++){
ednum[i] = i;
T[i] = 0;
}
Kruskal(K, k, G_aux, ednum, T);
/*最小木に含まれる頂点を全てUに追加*/
for(i = 0; i<K*(K-1)/2; i++){ //各頂点が最小木に含まれればU0_checkに1を代入
if(T[i] == 1){
u = G_aux[i].end1;
v = S[G_aux[i].end2];
U0[S[u]] = 1;
//printf("%d!\n",S[u]);
U0[v] = 1;
//printf("%d!\n",v);
while(p[u][v] != S[u] && p[u][v] != v){
U0[p[u][v]] = 1;
//printf("%d!\n", p[u][v]);
v = p[u][v];
}
}
}
// k = 0;
// for(i=0; i<N; i++){ //U_checkに1が入っている頂点をUに追加
// if(U0_check[i] == 1){
// U0[k] = i;
// k++;
// }
// }
// U0_num = k; //Uの要素数を格納
/*②タブー探索に必要なものを初期化*/
/*UbとUの初期化*/
for(i=0; i<N; i++){
Ub[i] = U0[i];
U[i] = U0[i];
}
/*f(Ub)を計算*/
best_score = function( N, M, edge, ednum, U0, T);
high_score = best_score;
printf("\nfirst_score = %d\n", best_score); //デバグ用print
/*タブー集合の初期化*/
for(i=0; i<t_list_size; i++){
taboo[i] = inf;
}
/*ランダムシードの設定*/
srand(0);
/*ここでタブー探索に必要なものの初期化は終わり*/
end_t = clock();
utime = (end_t-start_t)/CLOCKS_PER_SEC;
score=0;
change=0;
while (utime <= time_limit) {
/*③近傍探索*/
change=neighborhood(edge,ednum,U,Umin,Is,N,M,&score,T);
//printf("change=%d\n",change);
end_t = clock();
utime = (end_t-start_t)/CLOCKS_PER_SEC;
if (utime > time_limit){break;} /* 制限時間を過ぎたら終了 */
else {
/* ④タブーであるかの確認 */
if(score <= high_score){
for(i=0; i<N; i++){
Ub[i] = Umin[i];
U[i] = Umin[i];
}
high_score = score;
if(high_score < best_score){
best_score = high_score;
printf("current_score = %d\n", best_score);
}
if(check_taboo(taboo, change)){ //もし、変更箇所が禁じ手であったら
//その部分をタブーリストの一番新しい記録に移動する
for(i=t_list_size-1; i>=0; i--){
if(taboo[i] == change){
for(j=i; j>=1; j--){
taboo[j] = taboo[j-1];
}
taboo[0] = change;
}
}
}
}
else{
if(check_taboo(taboo, change)){ //もし、変更箇所が禁じ手であったら
// 新しい初期解 U を求めるためにランダムリスタートする。
random_restart(N, S, K, U);
//initial_solution(edge, N, M, K, *d, *p, S, U);
high_score = function( N, M, edge, ednum, U, T);
//タブーリストの初期化
for(i=0; i<t_list_size; i++){
taboo[i] = inf;
}
}
else{
for(i=0; i<N; i++){
U[i] = Umin[i];
}
//changeをタブーに入れる(全体を移動する)
//溢れた場合は、一番古い記憶を削除する
for(i=t_list_size-1; i>=1 ; i--){
taboo[i] = taboo[i-1];
}
taboo[0] = change;
}
}
}
}
/* 結果を出力 */
printf("\n"); /*この行は消さないで!(画面の調整のため)*/
printf("best_score=%d\n",best_score);
/*tabooの確認*/
// printf("taboo = ");
// for(i=0; i<t_list_size; i++){
// printf("%d ",taboo[i]);
// }
// printf("\n");
return 0;
}
/* ========================以下、必要な関数=================================*/
/*以下、クラスカル法に関与する関数*/
void Kruskal(int N, int M, struct edge_data *edge, int *ednum, int *T){
/* n: 頂点数, m: 辺数, edge: 辺データ, ednum:昇順における辺の番号, */
/* T: 最小木を表す配列, T[i] = 1 ⇔ 最小木は辺 i を含む */
int i;
int u,v,w;
int UnionIsConducted;
int p[maxN], rank[maxN];
int W[maxM]; /* 辺の重みを格納する配列 */
for (i=0; i<M; i++){
W[i] = edge[i].weight;
ednum[i] = i; /* 配列 W と ednum にデータを格納 */
}
quicksort(W, ednum, 0, M-1);
for(i=0; i<M; i++){
T[i] = 0;
}
for (u=0; u<N; u++){
make_set(p, rank, u);
}
for (i=0; i<M; i++){
u = edge[ednum[i]].end1;
v = edge[ednum[i]].end2;
UnionIsConducted = set_union(p, rank, u, v);
if(UnionIsConducted){
T[ednum[i]] = 1;
}
}
}
void make_set(int *p, int *rank, int x){
p[x] = x;
rank[x] = 0;
}
int set_union(int *p, int *rank, int x, int y){
int u, v;
u = find_set(p, x);
v = find_set(p, y);
if( u != v ){
link(p, rank, u, v);
return 1;
}
return 0;
}
int find_set(int *p, int x){
int y,r,z;
y = x;
y = p[y];
while (y != p[y]){
y = p[y];
}
r = y;
y = x;
while (y != r){
z = p[y];
p[y] = r;
y = z;
}
return (r);
}
void link(int *p, int *rank, int x, int y){
if (rank[x] > rank[y]){
p[y] = x;
} else {
p[x] = y;
if (rank[x] == rank[y]){
rank[y] = rank[y] + 1;
}
}
}
void quicksort(int *A, int *ednum, int p, int r){
int q;
if( p < r ){
q = partition(A, ednum, p, r);
quicksort(A, ednum, p, q);
quicksort(A, ednum, q+1, r);
}
}
int partition(int *A, int *ednum, int p, int r){
int x,i,j,tmp;
x = A[p];
i = p;
j = r;
while(1){
while(A[j] > x){
j--;
}
while(A[i] < x){
i++;
}
if(i < j){
tmp = A[i];
A[i] = A[j];
A[j] = tmp;
tmp = ednum[i];
ednum[i] = ednum[j];
ednum[j] = tmp;
j--; i++;
}
else{
break;
}
}
return j;
}
/*f(U)の関数*/
int function(int N, int M, struct edge_data *edge, int *ednum,int *IU, int *T){
/* n: 頂点数, m: 辺数, edge: 辺データ, ednum:昇順における辺の番号, */
/* T: 最小木を表す配列, T[i] = 1 ⇔ 最小木は辺 i を含む */
/*IU: 頂点uが頂点集合Uに入っているとき、IU[u]=1として表現する。入っていないときはIU[u]=0とする。*/
int i,k;
int u,v,w;
int UnionIsConducted;
int p[maxN], rank[maxN];
int W[maxM]; /* 辺の重みを格納する配列 */
int wsum; /*選んだ辺の重みの和*/
int count; /*辺の数をカウント*/
int u_count;
for (i=0; i<M; i++){
W[i] = edge[i].weight;
ednum[i] = i; /* 配列 W と ednum にデータを格納 */
}
count=0;
u_count=0;
wsum=0;
quicksort(W, ednum, 0, M-1);
for(i=0; i<M; i++){
T[i] = 0;
}
for (u=0; u<N; u++){
if(IU[u]==1){
/*頂点Uが入っているときにmake_set を行う。*/
make_set(p, rank, u);
u_count++;/*Uに含まれる頂点数をカウントを1増やす*/
}
else{}
}
for (i=0; i<M; i++){
u = edge[ednum[i]].end1;
v = edge[ednum[i]].end2;
if(IU[u]==1 && IU[v]==1){/*u,vが頂点集合Uに入っているとき*/
UnionIsConducted = set_union(p, rank, u, v);
if(UnionIsConducted){
T[ednum[i]] = 1;
count++;/*選ばれた辺の数を1増やす*/
wsum=wsum+edge[ednum[i]].weight;
}
}
}
/*ここから戻り値を決める操作を行う*/
/*選ばれた辺の数をcount,Uの頂点数をu_count,選んだ辺の重みの和をwsumに格納*/
u_count=u_count-1;
if(count==u_count){
k=wsum;
}
else if(count<u_count){
k=inf;
}
else{/*上記以外はエラーとして処理*/
printf("error:f(U)\n");
k=-1;
}
return k;
}
/*以下、ダイクストラ法の関数*/
void dijkstra(int v0, int N, int M, struct edge_data *edge, int *d, int *p){
int Lmat[maxN][maxN]; /* 重み行列を表す変数 */
int adr[maxN];
int hsize; /* ヒープに格納された頂点の数 */
int i,w,u,v,len;
struct cell Heap[maxN];
for (u=0; u<N; u++){ /* 重み行列の初期化 */
for (v=0; v<N; v++){
Lmat[u][v] = inf;
}
}
for (i=0; i<M; i++){
u = edge[i].end1;
v = edge[i].end2;
len = edge[i].weight;
Lmat[u][v] = len;
Lmat[v][u] = len;
}
for (u=0; u<N; u++){ //dとpの初期化
d[u] = inf; p[u] = NIL; adr[u] = NIL;
}
d[v0] = 0; p[v0] = NIL; //ダイクストラ法を開始する頂点の設定
hsize = 0;
hsize++;
Insert(Heap, hsize-1, d[v0], v0, adr);
while(1){
if(hsize == 0) break; //Heapが空か考える
v = Heap[0].vertex;// Aの中でdの値が最小の頂点を返す。
Delete_min(Heap, hsize, adr);
hsize--;
for(i=0; i<N; i++){
if(Lmat[v][i]!=inf){
w = i;//vに隣接するすべてのwについて
if(d[w]==inf){
d[w] = d[v] + Lmat[v][w];
p[w] = v;
hsize++;
Insert(Heap, hsize-1, d[w], w, adr);
}
else if(d[w]>d[v]+Lmat[v][w]){
d[w] = d[v] + Lmat[v][w];
p[w] = v;
decrease_key(Heap, hsize-1, d[w], adr);
}
}
}
}
}
int parent(int i){
return (i-1)/2;
}
int right(int i){
return 2*i+2;
}
int left(int i){
return 2*i+1;
}
void Insert(struct cell *H, int i, int a, int v, int *adr){
H[i].key = (-1)*a;
H[i].vertex = v;
Upheap_Sort(H, i, adr);
}
void Upheap_Sort(struct cell *H, int i, int *adr){
int tmp;
int u = i;
while(u>0 && H[parent(u)].key<H[u].key){
tmp = H[u].key;
H[u].key = H[parent(u)].key;
H[parent(u)].key = tmp;
tmp = H[u].vertex;
H[u].vertex = H[parent(u)].vertex;
H[parent(u)].vertex = tmp;
tmp = adr[H[u].vertex];
adr[H[u].vertex] = adr[H[parent(u)].vertex];
adr[H[parent(u)].vertex] = tmp;
u = parent(u);
}
}
void Downheap_Sort(struct cell *H, int i, int *adr){
int tmp;
int u=0;
int l, r;
do{
if(left(u)<=i){
l = left(u);
}
else{
l = u;
}
if(right(u)<=i){
r = right(u);
}
else{
r = u;
}
if(H[u].key>=H[l].key && H[u].key>=H[r].key) break;
if(H[l].key>H[r].key){
tmp = H[l].key;
H[l].key = H[u].key;
H[u].key = tmp;
tmp = H[l].vertex;
H[l].vertex = H[u].vertex;
H[u].vertex = tmp;
tmp = adr[H[l].vertex];
adr[H[l].vertex] = adr[H[u].vertex];
adr[H[u].vertex] = tmp;
u = l;
}
else{
tmp = H[r].key;
H[r].key = H[u].key;
H[u].key = tmp;
tmp = H[r].vertex;
H[r].vertex = H[u].vertex;
H[u].vertex = tmp;
tmp = adr[H[r].vertex];
adr[H[r].vertex] = adr[H[u].vertex];
adr[H[u].vertex] = tmp;
u = r;
}
}while(!(u==l && u==r));
}
void decrease_key(struct cell *H, int i, int a, int *adr){
H[i].key = a;
Upheap_Sort(H, i, adr);
}
int Delete_min(struct cell *H, int i, int *adr){
int v;
v = H[0].vertex;
adr[v] = NIL;
if(i > 1){
H[0].key = H[i-1].key;
H[0].vertex = H[i-1].vertex;
adr[H[0].vertex] = 0;
Downheap_Sort(H, i-2, adr);
}
return v;
}
/*以下、タブーリストから禁じ手を行っていないか確認する関数*/
int check_taboo(int *taboo, int change){
int i;
for(i=0; i<t_list_size; i++){
if(taboo[i]==change){
return 1;
}
}
return 0; //タブーであれば1、タブーでなければ0を返す
}
/*以下の関数は、近傍を探索するコードです。*/
/*changeには、追加、または削除した頂点の値が入る.*/
int neighborhood(struct edge_data *edge, int *ednum,int *U, int *Umin, int *Is, int N,int M, int *score,int *T){
int Iutemp[maxN];
int Iutemp2[maxN];
int i,j,x,y,z,k;
int change;
y=inf;
k=0;
for(i=0;i<N;i++){
Iutemp2[i]=0;
}
for(i=0; i<N; i++){
if(Is[i]==0){
for(j=0; j<N; j++){
Iutemp[j]=U[j];
}
if(U[i]==0){
Iutemp[i]=1;
change=i;
}else{
Iutemp[i]=0;
if(i==0){
change=300;
}else{
change=-i;
}
}
x=function(N, M, edge, ednum, Iutemp,T);
Iutemp2[i]=x;
if(x<y){
for(j=0; j<N; j++){
y=x;
Umin[j]=Iutemp[j];
k=change;
}
}
}
}
*score=y;
return k;
}
/*以下、ランダムリスタート用のコード*/
void random_restart(int N, int *S, int K, int *U){
int i;
for(i=0; i<N; i++){ //初期化
U[i] = 0;
}
for(i=0; i<K; i++){ //Sに含まれる頂点をUに追加
U[S[i]] = 1;
}
for(i=0; i<N; i++){ //Uに含まれる頂点をランダムに追加
if(rand()%2==0){
U[i] = 1;
}
}
}
(終わり)