金融理論（CAPM）で世界のコロナ新規感染者の推移を分析してみる

まずはお約束（ディスクレーマー）

私は経済学者でも感染学者でもなく、ただのゆるふわデータサイエンティストです。
ここに書いてあることは「ふーんそんな考え方もあるのかな」くらいの気持ちで鼻くそほじりながら読んでください。
本記事は何らかの行動を促すものでは全くありません。
あくまでも、数理モデルとPythonプログラミングに関する資料の一環としてご覧ください。

モチベーション

世界中の株式はβ（ベータ）でつながっている

金融とくに株式投資の世界では、すべての株式はグローバルにつながっています。
いや、経済的な実態とか、サプライチェーンがつながってるとかどうとかって話ではなく、だいたい値動きが連動しているということです。
たとえば去年のコロナショックのときも、ほとんどの銘柄が一斉に売られて値下がりし、そしてその後ほとんどの銘柄が一斉に買われて値上がりしました。
これを金融の世界ではβ（ベータ）と呼び、ちなみにβで説明しきれない各銘柄固有の値動きはα（アルファ）なんて言います。
ちなみにこのβですが、業種ごと、銘柄ごとに多少異なります。全業種、全銘柄にわたって平均をとると概ね1ですが、たとえば、エネルギーなど景気敏感株のβは1（＝平均）より大きく、生活必需品など景気に左右されにくい株のβは1より小さい傾向にあることが確認されています。

世界中のコロナもたぶんβでつながっている気がした

いや、デルタ株とかラムダ株とか、ギリシャ文字がよく使われるからって、安直に金融に結び付けたわけじゃありませんよ😅
えっ、デルタ「株」とかラムダ「株」とかいうから連想したんだろうって？…そんなわけないじゃないですか💦
経済がグローバル化している現代、人流もグローバル化しています。日本に住むアメリカ人もいっぱいいるし、フランスに旅行にいく中国人の団体旅客もいる。国際的な人流は２０年前、３０年前より確実に増えているはずです。もちろん、今はロックダウンなり緊急事態宣言なりで多少は抑制気味でしょうが、それでも世界中の人々の人流が全く無くなることはありえませんし、今後も徐々に回復していくでしょう、
したがって、いくつかの例外国（非常に厳しいロックダウンを行っている中国等）を除き、「世界中で感染者数が増えている／減っているにも関わらず、どこどこの国だけ全然感染者が増えない／減らない」ということは考えにくく、多少のタイムラグはあれど、基本的には世界のトレンドに回帰するものと考えられます。
そこで、今回は新規感染者数の変動に着目し、世界平均に対する各国のコロナ感応度＝βを計算してみようと思います。

数理モデル

株式の場合

ランダムウォークと同様、株価水準そのもので相関をとるといわゆる疑似相関が起きてしまうことがわかっているため、まず、日々の株価の変化率を計算します。

r_t^i = \frac{P_t^i}{P_{t-1}^i} - 1

ここで、Rは「リターン」すなわち変化率、Pは株価そのもの、tは時刻、iは銘柄を指します。

各銘柄のリターンを計算したら、次に各銘柄のリターンの世界平均を計算します。
本当は時価総額で加重平均をとる必要がありますが、ここでは簡易的に単純平均で済ませておきます。

r_t^{World} = \frac{1}{N} \sum_{i=1}^N r_t^i

ここで、Nは銘柄数を指します。

そして、各銘柄のリターンを被説明変数、世界平均を説明変数とする回帰分析を実施します。
これを金融の世界では**CAPMモデル（Capital Asset Pricing Model）**と呼んでいます。

r_t^i = \hat\beta^i r_t^{World} + \hat\alpha^i + \epsilon_t^i

ハットつきの変数が、回帰分析で推定されるものです。すなわち、回帰分析の傾きβと切片αで、それらで表現できないお釣りが残差εです。
そして、このβこそ、世界の株式の平均リターンに対する銘柄iの株価リターン感応度です。
今回は、世界の新規感染者リターンに対する国iの新規感染者リターン感応度を求めたい、ということになります。

さて、この回帰分析モデルがそもそも適切かどうかは、モデルが吐き出す値が実際の値にどれだけ近いか（当てはまりがよいか）で評価され、典型的な指標としては決定係数$R^2$が挙げられます。銘柄iの決定係数$R^2_i$は、いくつか流派がありますが、たとえば以下のように求めることができます。

\begin{align}
R^2_i &=& 1 - \frac{{\rm{Var}}[r_{actual}^i - r_{model}^i]}{{\rm{Var}}[r_{actual}^i]} \\
&=& 1 - \frac{{\rm{Var}}[\epsilon^i]}{{\rm{Var}}[r^i]}
\end{align}

ここで${\rm{Var}}[X]$は変数Xの分散、ばらつきです。
決定係数の上限は1（モデル値と実測値が完全に一致している）で、だいたいの場合は0～1の値に収まり、%表記で語られることが多い（0.8なら80%など）ですが、あんまりひどい場合はマイナスになることもあり、そのような場合は適用するモデル自体を再検討したほうがよいということになります。

コロナの場合

内閣官房がJSON形式のデータを日々更新してくれているのでそこからデータをもってきます。

このサイトにJSONデータへのリンクがあります。

このJSONデータには、各国の日々の「累積感染者数」および「死亡者数」が記載されています。

まず、累積感染者数から、新規感染者数を求めます。日々の数字の差分をとるだけです。

NewCase_t^i = Infection_t^i - Infection_{t-1}^i

NewCaseが新規感染者数、Infectionが累積感染者数、tが時点、iが国です。

この新規感染者数は、よく知られているように、「波」を形成します。つまり、昨日3000人が新規感染したのに、次の日にいきなり0になることはなく、近い値をとります、言い換えれば、新規感染者数は連続的に変化するということです。
また、「新規」感染者数は、増えることも減ることもあります。この点でも、株価と同じです。
一方、「累積」感染者数だと、増えることはあっても減ることはないので、累積感染者数を株価に照らし合わせることより、新規感染者数のほうが適切だと考えました。

新規感染者数を計算したら、株価と同様に、変化率を求めます。すなわち「新規感染者数リターン」です。
ただし、ここで、技術的にいくつか注意すべき事項があります。
まず、株価と異なり、新規感染者数は理論上0となりえますし、内閣官房の累積感染者数から差分で求めた新規感染者数にはマイナスの値も現れてくるので、ここでは数学的な便宜のために0以下の数字は1（人）に置き換えておきます。

\widetilde{NewCase_t^i} = \left\{
\begin{array}{ll}
NewCase_t^i &  NewCase_t^i > 0 \\
1 & NewCase_t^i \leq 0
\end{array}
\right.

また、感染者数の統計は週レベルの季節性（たとえば、月曜日は少なめに出やすく、木曜日は多めに出やすい等）があるので、7日移動平均をとっておきます。

\mu_7[\widetilde{NewCase_t^i}] = \frac{1}{7}\sum_{s=t-6}^t \widetilde{NewCase_s^i}

さらに、2020年のコロナ初期など検査体制が整備されておらず統計も不十分であった時期には、非常に極端な値が出やすく外れ値となってしまうケースが散見されるので、日ごとに国間でクロスセクション方向に下限10%/上限90%の丸め処理（winsorize）、および、各国内で時系列方向に下限1%/上限99%の丸め処理を実施しました¹。
丸め処理は便宜的に以下のように記載しておきます。

\omega_C^{L/U}[X], \omega_T^{L/U}[X]

CはCrossSection、TはTimeSeriesを表し、それぞれ変数Xをクロスセクション方向および時系列方向に下限L%/上限U%でwinsorizeしたものを指すことにします。

以上のような技術的加工をした上で、「新規感染者数リターン」を計算します。

r_t^i = \frac{\omega_T^{1/99}[\omega_C^{10/90}[\mu_7[\widetilde{NewCase_t^i}]]]}{\omega_T^{1/99}[\omega_C^{10/90}[\mu_7[\widetilde{NewCase_{t-1}^i}]]]} - 1

このようにして各国の新規感染者数リターンを計算したら、あとの流れは同様で、新規感染者数リターンの世界平均を計算し、感応度分析をすればよいわけです。

実際にやってみた。

累積感染者数のトップ10国＋日本

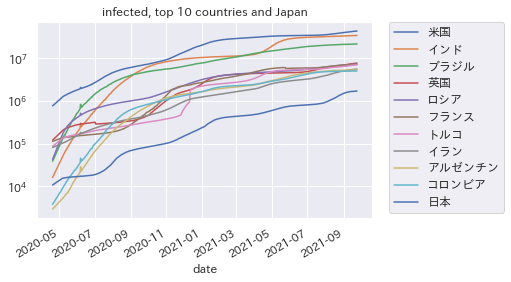
感染者数も複利で増えますから、対数グラフでみるのが適切です。
アメリカとインド、ブラジルが3強ですね。

新規感染者数のトップ10国＋日本

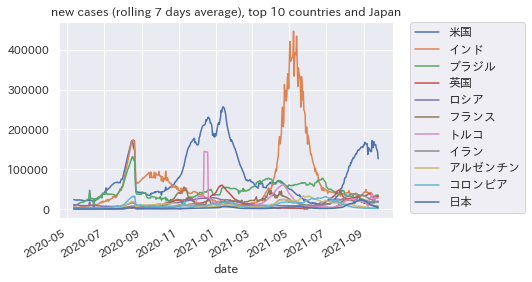
こっちはテレビや新聞でよく見るグラフなので、イメージをつかみやすいよう、対数グラフでなく通常の目盛りにしておきました。
新規感染者数のグラフでは、インドの感染爆発が目立ちます。

新規感染者数リターンのトップ10国＋日本

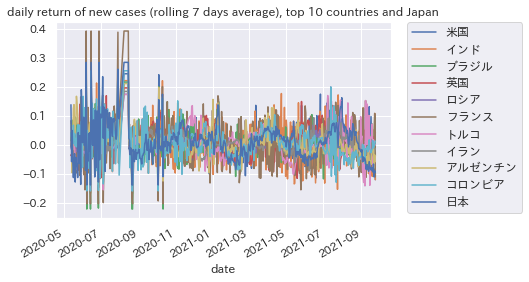
ここまでくると株価リターンに近い見た目になりますが、これでもまだ時系列の連続性が残っている（青色の日本がわかりやすい）こと、2020年のコロナ初期は極端な値が出ていることが見て取れます。

新規感染者数の世界平均および中央値

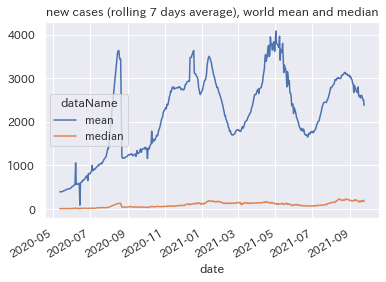
平均と中央値でかなり挙動が違います。
肌感覚的には、平均のほうが実感に近そうです。

新規感染者数リターンの世界平均および中央値

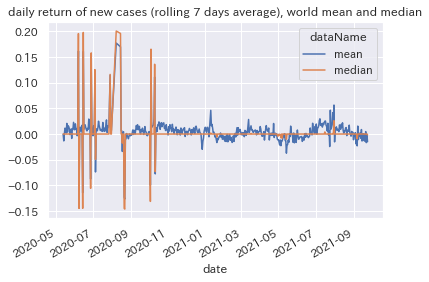
リターンにしてみても、中央値よりも平均値のほうが扱いやすそうです。

コロナβの分布

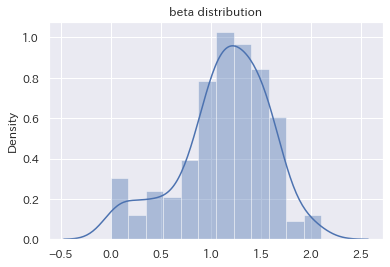
各国のβの中央値は1.2弱でした。1より若干大きいですが、概ね1を中心に分布していると考えてよさそうです。
そして、βが負、つまり、世界平均と逆相関となるような国はありませんでしたが、βがほぼ0、すなわち、世界平均とほぼ無相関になるような国も存在していることがわかります。

コロナβ（上位5国＋下位5国）

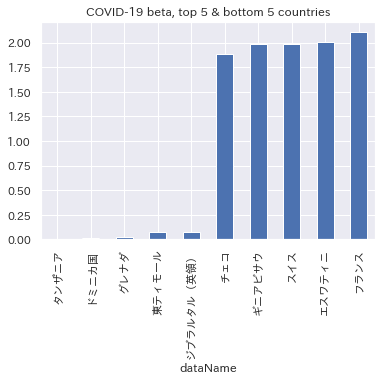
こちらは新規感染者数の水準にかかわらず、感応度が高い国と低い国を記載しています。
感応度が特に高い国として、フランスやスイスなどが入っています。これらの国のベータは2を超えています。
すなわち、世界的に新規感染者数が+5％増えたとき（たとえば新規感染者数が1000人→1050人になったとき）、これらの国では新規感染者数が2倍の+10%（たとえば新規感染者数が3000人→3300人のようになる）となる傾向がある、と解釈することができます。
一方、感応度が特に低い国としては、タンザニアやドミニカなどのβがほぼ0みたいに見えてますが、情報がそもそも少ない国なので。。数字の信ぴょう性も含め、話半分くらいに捉えておいたほうが無難かもしれません。

コロナβ（新規感染者数のトップ10国＋日本）

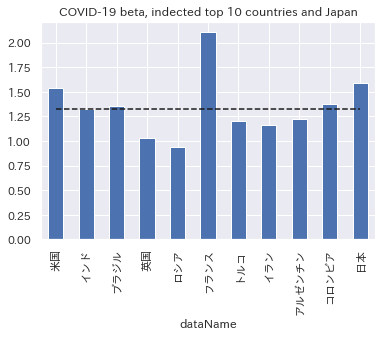
新規感染者数が多い国は、水準だけでなく、その感応度も平均的に高いことがわかります。
実際、トップ10国＋日本のβの中央値（グラフ点線）は1.3ほどになっており、世界の中央値1.2を超えています。
特に、アメリカや日本は、その平均すら超えてβが1.5以上となっており、世界のコロナ感染の動きにより強く反応していることがわかります。
背景として、アメリカや日本、フランスなどが、ほかの国と比べて比較的、人流抑制には緩和的であろうことが想像されます（ただの想像ですが）。

決定係数の分布

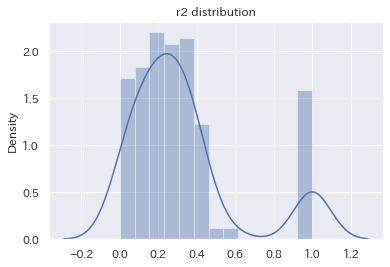
各国の決定係数の中央値は0.25（25％）強でした。
水準としては、株式の個別銘柄もこんなもんなので、モデルとしては筋が良いほうだと考えてよさそうです。

決定係数（新規感染者数のトップ10国＋日本）

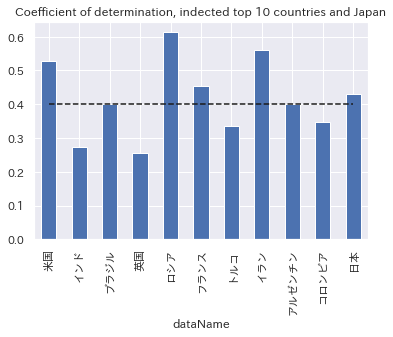
新規感染者が多い国は、水準だけでなく、決定係数も平均的に高いことがわかります。
言い換えると、各国固有の事象というより、グローバルなトレンドにひっぱられる部分が大きいということです。
トップ10国＋日本の決定係数の中央値（グラフ点数）は0.4（40％）となっており、全世界の中央値と比べて15ポイントほどモデルのあてはまりがよい、モデルによる説明力が大きい結果となりました。
ちなみに、βの水準の大きさではフランスが抜きん出ていましたが、決定係数という観点では必ずしもトップではないことには留意が必要です。
感応度が高いということと、説明力が高いということは、まったく別の話です。

新規感染者数リターンの散布図vs世界平均（フランス、中国、日本）

βと決定係数が若干ごっちゃになってきてしまう人もいるかもしれないので、散布図をみて視覚的に理解しましょう。
横軸が日々の新規感染者数リターンの世界平均で、縦軸が各国のリターンです。
この散布図の点を最もよく近似する直線こそがCAPMモデルであり、フランスは日本や中国と比べて近似直線の傾きβが大きく、逆に中国はβが小さいことがわかります。
また、フランスや日本は近似直線の近くに点が集まっている一方で、中国は近似直線からどっ外れている点が散見され、決定係数$R^2$が相対的に低いこともわかります。

中国の場合

新規感染者数トップ10国に出てこなかった中国ですが、新規感染者数βは1.13で1より若干大きい一方、上記の散布図でみた通り、決定係数は0.16(16%)と非常に小さい結果となりました。
厳しいロックダウンで他国との国交を断絶していたり、グローバルのトレンドとは異なる特有の推移をしている、と考えることができそうです。

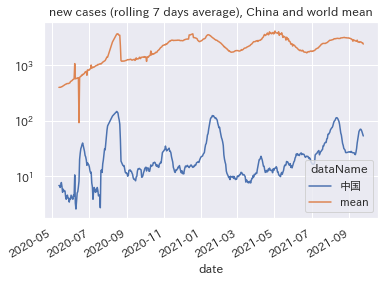
新規感染者数の推移

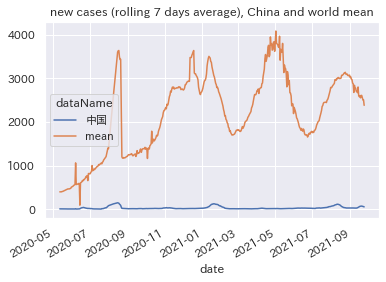
新規感染者数の推移（普通の目盛りだと見づらいので対数目盛）

2021/11/08追記：オリンピック前後の日本

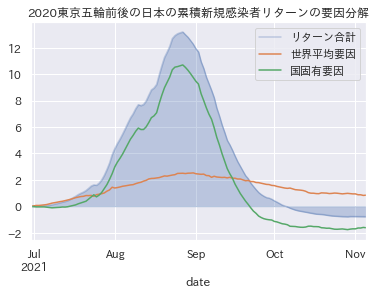
2021/6/30以降の日本の新規感染者数リターンについて、世界平均要因（β）と国固有要因（α）に分解しました。
こうして見ると、オリンピック開催期間中は、世界での新規感染に対する感応度以上に感染者が増えているように見えますね。。
一方、オリンピック後は、日本だけが世界の中でも特異なほど新規感染者数が減少していることから、国固有要因（α）がマイナス圏に突入していることもわかります。
オリンピック開催期間中の感染爆発は、定性的には「日本に限らず世界中で第五波が広がっていたから」ということになっていますが、CAPMモデルを通して定量的に分析すると、「とはいえ、世界の感染増加に対する感応度以上に感染増加していた可能性がある」とみることもできますね²。

まとめ

• 株式の世界で用いられるCAPMモデルは、コロナの新規感染者数の推移の表現にもある程度は適用できそうであることがわかりました。
• 新規感染者数にCAPMのβを応用することにより、各国政府の感染対策の厳しさ（緩さ）をある側面で定量化できそうなことがわかりました。
• 同様に、CAPMの決定係数を応用することにより、各国政府の感染対策のうち特に国交政策の厳しさ（緩さ）や、他国との感染対策の足並みをある側面で定量化できそうなことがわかりました。

Pythonコード

Google Colabで作ったので適宜ご覧ください。

1. winsorizeについてもう少し丁寧に補足（というより数式化）しておくと、N個のデータからなる変数X（簡単のため値の重複はないものとする）を小さい順に並べ、Xの中の任意の値xに対してその順位を返す関数 ${\rm{rank}}_X(x)=i ~ (1 \leq i \leq N)$ を%表記に直した ${\rm{rank}}_X^{%}(x)={\rm{rank}}_X^{%}(x)/N = i/N$ の逆関数 $({\rm{rank}}_X^{%})^{-1}(p)=x \Leftrightarrow {\rm{rank}}_X^{%}(x)=p ~ (0 \leq p \leq 1)$ を用いて、$\omega^{L/U}[X](x)= {\rm{min}}({\rm{max}}(x, ({\rm{rank}}_X^{%})^{-1}(L%)), ({\rm{rank}}_X^{%})^{-1}(U%))$と表すことができます。 ↩

2. ひつこいようですが、だからといって政府やオリンピック組織委員会のコロナ対策は不十分だとか言うつもりは全くありませんし、何よりこんなおもちゃモデルで判断するべきではありません。とはいえ、「このようなものの見方があるんだ」ということを理解すると、将来、色々なものが落ち着いて冷静に2021年を振り返ることができるようになった頃、ある程度真面目な定量モデルをつくって、当時の政策の妥当性を検討し、将来新たなパンデミックが起きたときに過去の経験を活かすことができる可能性があるんだ、と思えるようになりますね。 ↩