Go to Qiita Advent Calendar 2024 Top
LoginSignup
30
19

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 5 years have passed since last update.

JuliaAdvent Calendar 2018Day 21
@Dolphin7473(Dolphin7473)

Vicsek model：二次元自己駆動粒子系と相転移

Last updated at Posted at 2018-12-20


2018/12/21, 18:00
@goropikari さんにご指摘いただいた

  • 粒子間距離の計算で周期境界を考慮できていない
  • 近傍粒子の角度の計算で正負の打ち消しが生じている

問題を修正し，動画及び図を差し替えました．
@goropikari さん，ありがとうございます．

Julia Advent Calendar 2018，12/21日を担当します @Dolphin7473 です．

1. アクティブマターとVicsek model

Julia advent calendarはみなさんJulia言語自体に関する興味深い記事を書いておられますが，「数値計算にJulia使ってみた」程度の記事が一つくらいあってもいいだろう，と思い執筆してみました．1

アクティブマターとは，ごく簡単に言うと 自走する粒子（群） です．バクテリアなどの微生物のような，各々が勝手に動きまわる物体（群）の総称で，この10年程度で広まった呼び方です．簡単に読める日本語の紹介には

などがあります．

本記事では，アクティブマターの中でも最も簡単なモデルであるVicsek modelを二次元周期境界上で実装し，その性質をみます．先の物理学会誌の記事において，Vicsek modelは

一定の速度で任意の方向に進む点粒子を考え，個々の粒子はその周りの有限の範囲にいる粒子の平均の速度方向に動く相互作用を導入し，時々刻々，速度の向きに小さなノイズを与えた2

この記事の実装は，原著論文ではなくMicroswimmers Summer School 2015というサマースクールで用いられた講義ノートに基づいています．本記事，あるいは実装したプログラム中の変数はこの講義ノートと同じものを使っています．

1.1 アルゴリズム

$(x, y)\in[0,1]\times[0,1]$ の二次元領域に $N$ 個の粒子があるとします．初期条件として粒子の位置と角度が与えられ，どちらもランダムであるとします．

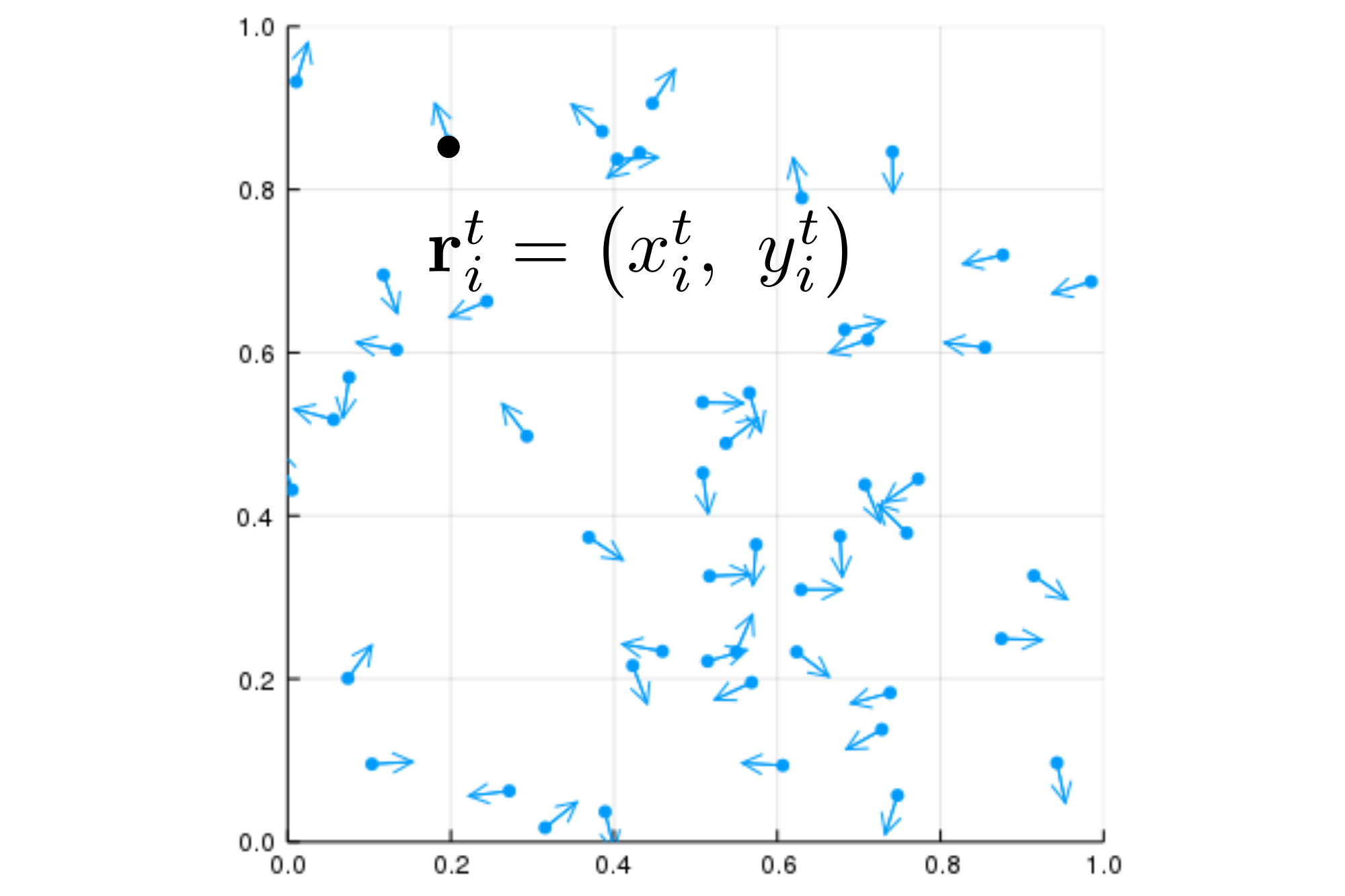
$i$ 番粒子の時刻 $t$ での位置を $\mathbf{r}_i^t$ と書くことにします．いま，2次元の系を考えているので，

\mathbf{r}_i^t = (x_i^t, y_i^t)



のように表せます．

これらの粒子は自分自身により駆動され，運動します．その速さを $v_0$ ，向きを単位ベクトル $\mathbf{s}_i^t$ と書きます．

簡単のため $v_0$ を定数とし，

v_0 = \mathrm{const.}

さらに全ての粒子に対し同じであるとします．

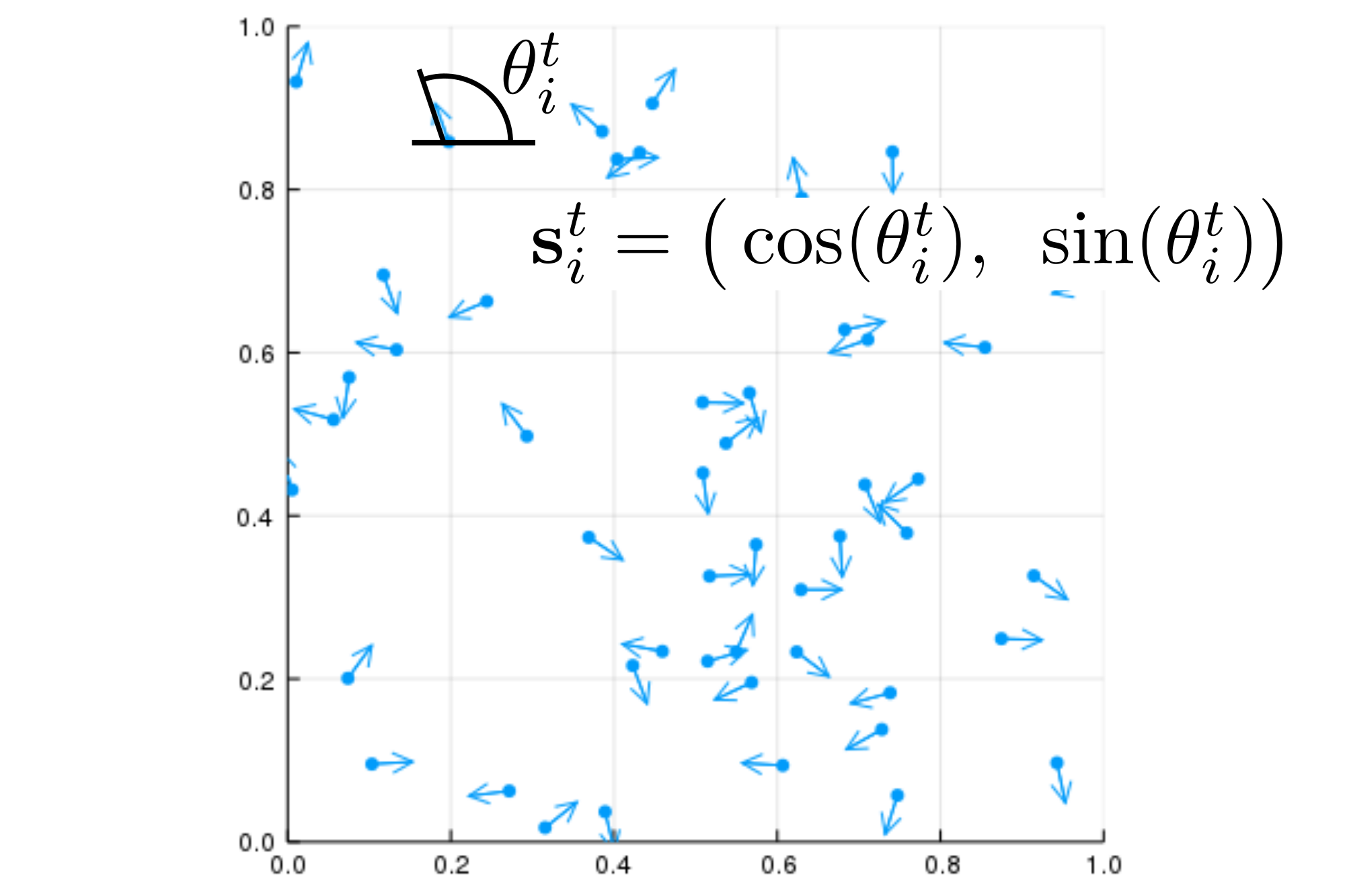
また，二次元の系に対して $\mathbf{s}_i^t$ は角度 $\theta$ で表すことができ，

\mathbf{s}_i^t = \big( \cos(\theta_i^t),~\sin(\theta_i^t) \big)



のように表せます．

次にこの系の時間発展を考えます．時刻 $t+\Delta t$ における粒子の位置 $\mathbf{r}_i^{t+\Delta t}$ を，

\mathbf{r}_i^{t+\Delta t} = \mathbf{r}_i^{t} +\Delta t v_0 \mathbf{s}_i^{t+\Delta t}

\left\{
\begin{array}{l}
x_i^{t+\Delta t} = x_i^{t} +\Delta t v_0 \cos (\theta_i^{t+\Delta t}) \\
y_i^{t+\Delta t} = y_i^{t} +\Delta t v_0 \sin (\theta_i^{t+\Delta t})
\end{array}
\right.

のように書きます．
この方程式を書き直すと，

\frac{ \mathbf{r}_i^{t+\Delta t} - \mathbf{r}_i^{t} }{\Delta t} = v_0 \mathbf{s}_i^{t+\Delta t}

となり，右辺が次の時刻ステップによって定まる陰解法の形であることが分かります．3

次の時刻ステップでの運動の向き $\mathbf{s}_i^{t+\Delta t}$ は，（自分自身を含む）近傍の粒子の配向の平均にノイズを添加したものとして，

\theta_i^{t+\Delta t} = \mathrm{Arg} \biggr[ \sum_j n_{ij}^t \mathbf{s}_j^t \biggr] + \eta \xi_i^t

と定義されます．ここで， $n_{ij}$ は $i$ 番粒子の近傍粒子に対して1，遠くの粒子に対して0となる結合行列，

n_{ij}^t = \left\{
\begin{array}{ll}
1 & \mathrm{if}~\big|\mathbf{r}_i^t-\mathbf{r}_j^t\big|<R_0 \\
0 & \mathrm{if}~\big|\mathbf{r}_i^t-\mathbf{r}_j^t\big|>R_0
\end{array}
\right.

で， $\xi_i^t \in [-\pi,\pi]$ は一様分布なホワイトノイズです．ノイズ振幅 $\eta$ がパラメータとして与えられています．

近傍の粒子配向によって自身の運動の向きが変化する様子を模式図として示します．

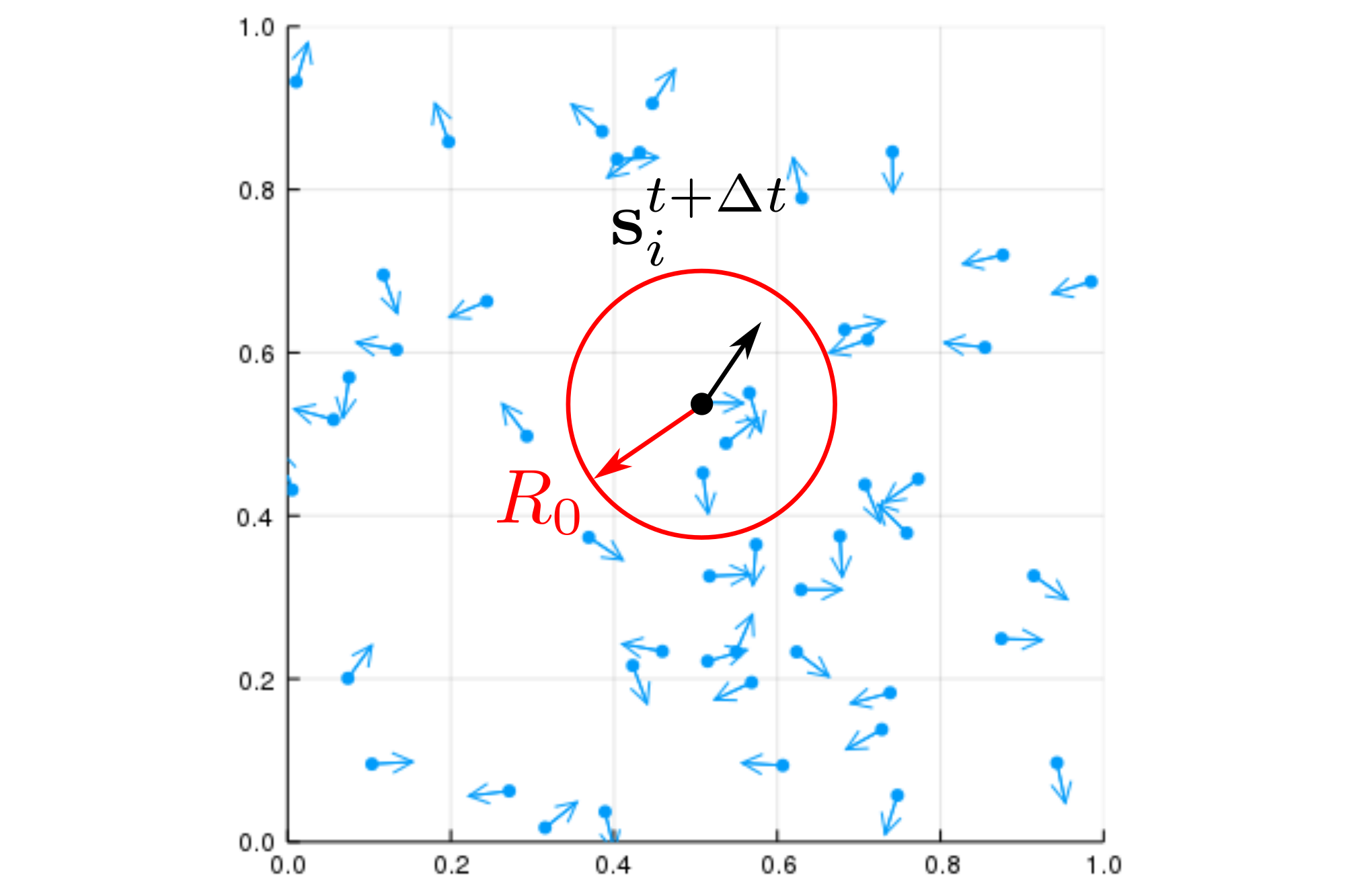
1.2 コントロールパラメータ

この系を支配するのは，次の3つのコントロールパラメータです．

コントロールパラメータ 文字
ノイズ振幅 $\eta$
粒子速さ $v_0$
粒子密度 $\rho=N/L^2$
ただし $N$ は粒子数， $L$ は系の一辺の長さ

今回は，この3つのパラメータのうち $v_0$ と $\rho$ を固定し，ノイズ振幅 $\eta$ が系に及ぼす影響をみていきます．

2. 実装

上節で述べたアルゴリズムを，二次元周期境界の領域に実装しました．
Vicsek_Model_julia

なお，Juliaによる数値計算については以下の記事に大変お世話になりました．
Juliaで数値計算　その1：コードサンプル〜基本的計算編〜
Julia言語と Plots + GR で複素関数のgifアニメーションを作る

この実装において，初期条件を与えた後の時間発展は

set_neighbour_list(param_,var_)
  # 結合行列の定義
set_neighbour_orientation(param_,var_)
  # 自身を含む近傍粒子の配向の平均を計算
set_white_noise(param_,var_)
  # 各時刻ステップで新たにノイズを定義
set_new_θ(param_,var_)
  # 近傍粒子の配向とノイズから，次の時刻ステップにおける角度を更新
set_new_r(param_,var_)
  # 次の時刻ステップにおける粒子位置を更新
set_periodic_bc(param_,var_)
  # 周期境界条件を満足させる
set_new_rθ(param_,var_)
  # 次の時刻ステップにおける変数を再定義する

で記述されています．

脚注3で述べた実装の変更は，角度と粒子位置の更新を入れ替えることで実装できます

3. 結果：ノイズ振幅と相転移

3.1 解析パラメータ

粒子群の配向を，極性秩序パラメータ（polar order parameter） $\mathbf{\varphi}(t)$ によって解析します．

\begin{align}
\mathbf{\varphi}(t) &= \frac{1}{N} \sum_{i=1}^N \mathbf{s}_i^t \\
    &= \frac{1}{N} \sum_{i=1}^N \big( \cos(\theta_i^t), \sin(\theta_i^t) \big)
\end{align}

この量は， 粒子の配向が揃っているほど大きく，ランダムな方向を向いているほど小さくなります．
以下では，このベクトル量の大きさ $\phi = \big| \mathbf{\varphi} \big|$とその時間平均 $<\phi>_t$ を指標として系を見ていきます．

3.2 系の時間発展と極オーダーパラメータ

コントロールパラメータのうち2つを以下のように固定します．

コントロールパラメータ 値
粒子速さ $v_0$ $0.05$
粒子密度 $\rho$4 $200$

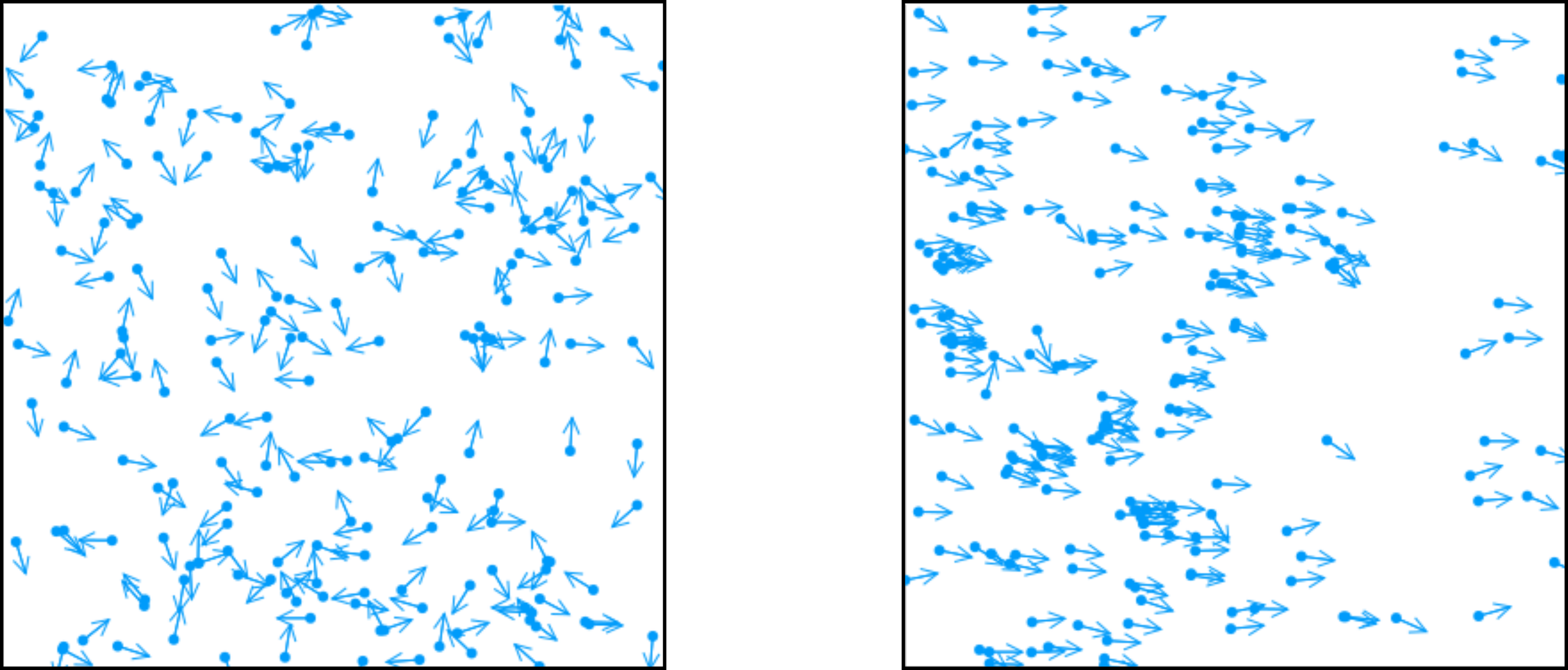
この上でノイズ振幅 $\eta$ を変化させて系を時間発展し，粒子の分布と極性秩序パラメータの大きさ $\phi$ の時間発展をアニメーションにしてみます．5

  • ノイズ振幅 $\eta=0.1$　
  • ノイズ振幅 $\eta=0.4$

ノイズ振幅 $\eta$ によって系の振る舞いに大きな差が生じることが分かります．$\eta$が小さい場合，系は時間発展と共に秩序状態に到達します．反対に$\eta$が大きい場合，系はランダムな状態のまま発展していきます．
次節では，この変化を時間平均した極性秩序パラメータから確認します．

3.3 ノイズ振幅と時間平均された極オーダーパラメータ

さまざまなノイズ振幅 $\eta$ に対して系を100000ステップ時間発展させ， $\phi$ の時間平均 $<\phi>_t$ を計算します．
その結果を下図に示します．



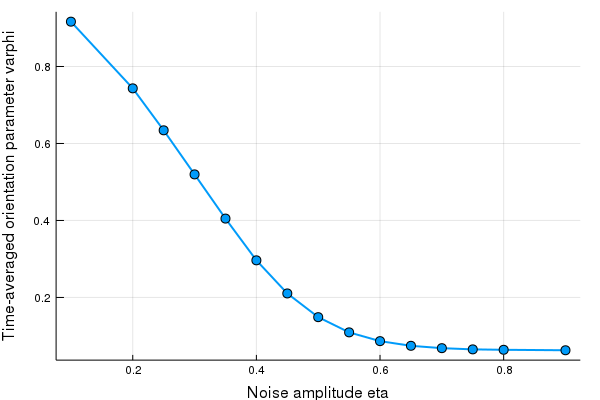
ノイズ振幅 $\eta$ が小さくなると系の対称性が破れ，秩序だった配向が達成されることが分かります．

4. さらなる解析・プログラムの改善

今回の記事ではVicsek modelの実装とごく簡単な解析（講義ノートのP.8，Fig. 2(a)まで）をおこないました．講義ノートにはこの他にも数多くの性質や系の拡張などがまとめられています．ぜひ実装にチャレンジしてみてください．

また，計算の高速化という観点からも，私の実装は優れたものではありません．特に，次に示す結合行列 $n_{ij}$ に関する部分が領域中の全粒子ペア探索となっており， $\mathcal{O}(N^2)$ の非常に非効率的な計算になっています．ここに粉流体の数値計算などで用いられているNeighbor listを実装することで，計算の高速化が可能だと思います． 誰か実装してPR投げてください．

[](

  • 他のコントロールパラメータについてのサーベイ
    • ここまで，3つのコントロールパラメータのうち2つを固定し，ノイズ振幅$\eta$の影響についてのみ見てきました．粒子速さ $v_0$ と粒子密度 $N$ 変化させることで，講義ノートに紹介されている他の性質についても確認できると思います．
  • 結合行列 $n_{ij}$ の計算の高速化
    • 現在の実装では，$n_{ij}$ を計算する際， $n_{ij}$ を用いて近傍粒子の配向を計算する際に領域中の全粒子を探索しています． ここに粉流体の数値計算などで用いられているNeighbor listを実装することで，計算の高速化が可能です．
      )
    """
    Calculate distance between two particles i and j,
    if distance is below threshold R_0, n_label (neighbour_label) have true.
    n_label of myself(tr(n_label)) is 1
    Also, calculate number of neighbour particles and store in var.n_sum
    """
    function set_neighbour_list(param,var)
        #=
        この処理がN^2を要する
        要高速化
        領域をR_0×R_0の矩形に分割し，隣接矩形でのみ検索する
        MPI
        =#
        for i=1:param.N
            n_col = 0  # Number of colums of n_label[i,:]
            for j=1:param.N
                # Calculate distance between two particles
                dx = abs(var.r[i,1] - var.r[j,1])
                dx = min(dx, 1.0 - dx)
                dy = abs(var.r[i,2] - var.r[j,2])
                dy = min(dy, 1.0 - dy)
                dist = hypot(dx, dy)
                if dist <= param.R_0
                    var.n_label[i,j] = true
                    n_col += 1
                else
                    var.n_label[i,j] = false
                end
            end
            var.n_sum[i] = n_col
        end
        # println("num. of neighbour=", n_sum.-1)  # exept myself
    end

    """
    Calculate one particle's neighbour orientation
    ψ will have [-π,π] value defined as
        ψ = Arg[Σ_j n_ij θ_j].
    """
    function set_neighbour_orientation(param,var)
        # var.ψ = zeros(param.N)
        #=
        この処理がN^2を要する
        要高速化
        領域をR_0×R_0の矩形に分割し，隣接矩形でのみ検索する
        MPI
        =#
        for i=1:param.N
            tmpx = tmpy = 0.0
            for j=1:param.N
                tmpx += var.n_label[i,j] * cos(var.θ[j])
                tmpy += var.n_label[i,j] * sin(var.θ[j])
            end
            var.ψ[i] = atan(tmpy, tmpx)
        end
    end

参考文献

Tamás Vicsek, et al., Novel Type of Phase Transition in a System of Self-Driven Particles，Arxiv版
Francesco Ginelli, The Physics of Vicsek Model
Juliaで数値計算　その1：コードサンプル〜基本的計算編〜
Julia言語と Plots + GR で複素関数のgifアニメーションを作る

  1. 数値計算advent calendarには24日に別のトピックで記事を執筆します ↩

  2. アクティブマターの非線形ダイナミクス
    系である，と説明されています．
    原著論文はPhysical Review Lettersに掲載され，引用回数が5000回（！）を超えています．Arxivにもアップされているのでオープンアクセスで読むことができます． ↩

  3. 陽解法により右辺を $\mathbf{s}_i^{t}$ で記述すればよいのではないか，という指摘がありえますが，実際，Vicsekらの最初の論文ではそのような定式化がなされています．後述するように，この差はどの段階で角度 $\theta$ を更新するか，ということにあり，実装上も変更は容易です．ただし，講義ノートには「この差によって系の本質的な性質は変わらない」とあるので，今回はこの定義を採用しています． ↩ ↩2

  4. $\rho$について，領域の大きさを $L=1$ に固定するならば粒子数 $N=200$ で代替可能です． ↩

  5. グラフ2枚を並べたアニメーションで矢印の幅が長さに対して大きすぎて不格好なのですが，調べてみると調整できない（あるいは不具合の）ようです．Plots.jl: arrows style in quiver()? ↩

30
19
2

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
30
19

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?