「正則化って何?」「scikit-learnってどう使うの?」
そんな疑問を持つ機械学習初心者の方に向けて、scikit-learnを使った機械学習アルゴリズムの基本をやさしく解説します。
本記事では、以下の内容を通して「正則化」や「ロジスティック回帰」「サポートベクトルマシン(SVM)」「決定木」など、実務でもよく使われる手法を一通り紹介し、Python(scikit-learn)での実装も実際に行います。
使用するデータは、特に記載がない限りすべてIrisデータセットです。
この記事は、書籍「Python機械学習プログラミング 達人データサイエンティストによる理論と実践」の第3章をベースにまとめたものです。
本記事では以下の流れで説明する。
Python version: 3.10.4
numpy version: 2.2.5
matplotlib version: 3.10.1
scikit-learn version: 1.6.1
1 正則化
scikit-learnの学習の前に、正則化について記述する。
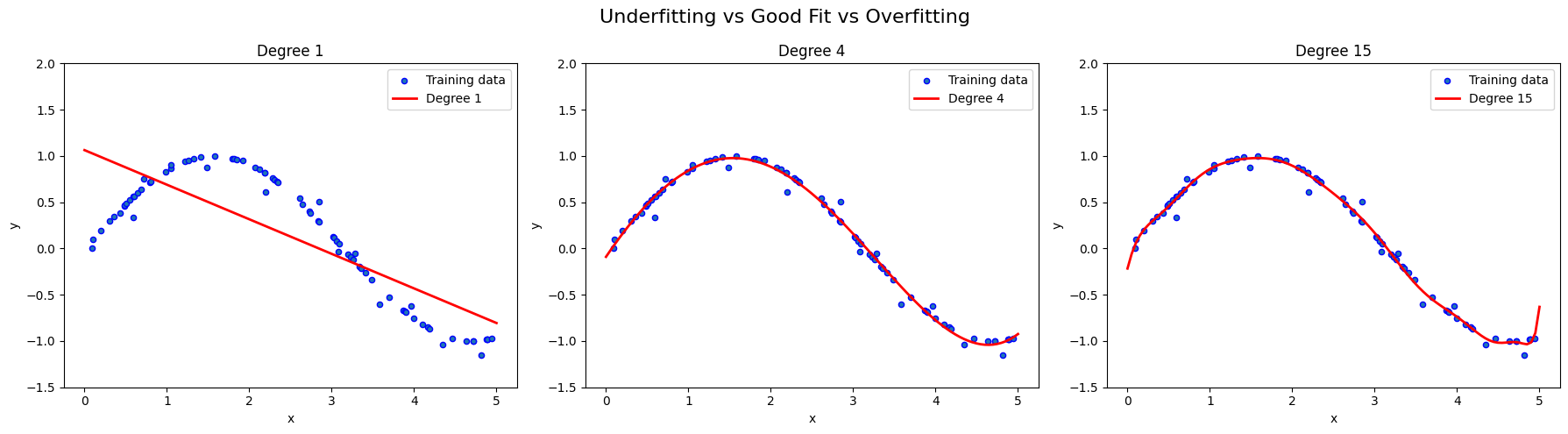
機械学習においては、訓練データの特徴を学びつつ未知のデータに対して高い予測精度をもつモデルを構築したい。そこで、問題となるのが過学習と学習不足である。
・過学習:訓練データでは上手く機能するが、未知のデータでは上手く機能しないモデル(汎用性が低い)。バリアンスが高い(high variance)と表現される。
・学習不足:逆に訓練データの特徴を十分に学んでおらず、訓練データに対しても未知のデータに対しても上手く機能しないモデル。バイアスが高い(high bias)と表現される。
一般にバリアンスとバイアスにはトレードオフがあるとされている。例えば、モデルが単純すぎて新しいデータにフィットしない場合(学習不足)、モデルを複雑にすることで、この問題が解消できる。その一方、モデルを過剰に複雑(高次の多項式など)にしてしまうと訓練データには正確にフィットするが、新しいデータに対してはノイズまで学習してしまい、予測が不安定になってしまう(過学習)。
コードを表示
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
# 乱数シード固定
np.random.seed(0)
# データ生成:非線形なデータ
X = np.sort(5 * np.random.rand(80, 1), axis=0) # 0から5の範囲で80個のデータ
y = np.sin(X).ravel() # sin関数に従う非線形データを使用
y[::5] += 0.5 * (np.random.rand(16) - 0.5) # 5個ごとに-0.25から0.25のノイズを追加
# 描画用データ
X_test = np.linspace(0, 5, 100).reshape(-1, 1) # テスト用に0から5の範囲で100個のデータ
# モデルの複雑さリスト(学習不足、適切、過学習)
degrees = [1, 4, 15]
# 描画
plt.figure(figsize=(18, 5))
for i, degree in enumerate(degrees, 1):
plt.subplot(1, 3, i)
model = make_pipeline(PolynomialFeatures(degree), LinearRegression()) # 多項式回帰モデル
model.fit(X, y)
y_pred = model.predict(X_test)
plt.scatter(X, y, edgecolor='b', s=20, label="Training data")
plt.plot(X_test, y_pred, color='r', linewidth=2, label=f"Degree {degree}")
plt.title(f"Degree {degree}")
plt.xlabel("x")
plt.ylabel("y")
plt.ylim(-1.5, 2)
plt.legend()
plt.suptitle("Underfitting vs Good Fit vs Overfitting", fontsize=16)
plt.tight_layout()
plt.show()
このバリアンスとバイアスのトレードオフ問題の解決策として、正則化がある。これは特徴量間の強い相関(共線性)や重みの偏りを抑制することで、データからノイズを取り除き最終的に過学習を防ぐ。極端なパラメータの重みにペナルティを科すとイメージすれば良い。最も一般的なものはL2正則化で以下の式をコスト関数に追加する。
$$
\text {L2正則化} = \frac{\lambda}{2} \|w\|^2 = \frac{\lambda}{2} \sum^{m}_{j=1}w^{2}_j
$$
$\lambda$は正則化パラメータで、この値が大きいほど正則化が強く作用する。
L2正則化を使用したいときは、この項をコスト関数に追加すれば良い。たとえば、ロジスティック回帰の場合は、
$$
\mathcal{J}(w, b) = -\frac{1}{N} \sum_{i=1}^{N} \left[ y^{(i)} \log(\hat{y}^{(i)}) + (1 - y^{(i)}) \log(1 - \hat{y}^{(i)}) \right] + \frac{\lambda}{2} ||w||^2
$$
L2正則化に対して、L1正則化もある。L1正則化は以下の式で書ける。
$$
\text {L1正則化} = \lambda |w|\ = \lambda \sum^{m}_{j=1}|w_j|
$$
L2正則化は大きな重みを持つ特徴量の重みを小さく抑えながら、あくまで全ての特徴量を使って学習を行う。それに対して、L1正則化は重みが0になるような特徴量が出ることもある。すなわち、重要な特徴量だけを残して学習をしたいならL1正則化を用い、それほど重要でもない特徴量を含めた全ての特徴量を学習に使いたいならL2正則化を使う。
| 比較項目 | L1正則化 | L2正則化 |
|---|---|---|
| ペナルティ内容 | 重みの絶対値の総和 | 重みの二乗和 |
| 効果 | スパース性(重みが0になるものが出る)を促進する → 特徴選択される | 大きな重みを小さく押さえる → すべての特徴量を少しずつ活かす |
| 使う場面 | 特徴量が多く、不要な特徴量を自動で除きたいとき | 特徴量は全部使いたいが過学習を防ぎたいとき |
| 実装例 | Lasso回帰(Lasso) | Ridge回帰(Ridge) |
2. ロジスティック回帰
ロジスティック回帰は分類問題に対して広く使われる手法で、二値問題で線形分離が可能な場合に特に有効だが、クラスが複数ある時にも対応できる。
1. まず、入力ベクトル$\mathbf{x}$に対して線形変換を行う
$$
z = \mathbf{w}^\top \mathbf{x} + b
$$
ここで、$\mathbf{w}$は重みベクトル、$b$はバイアス
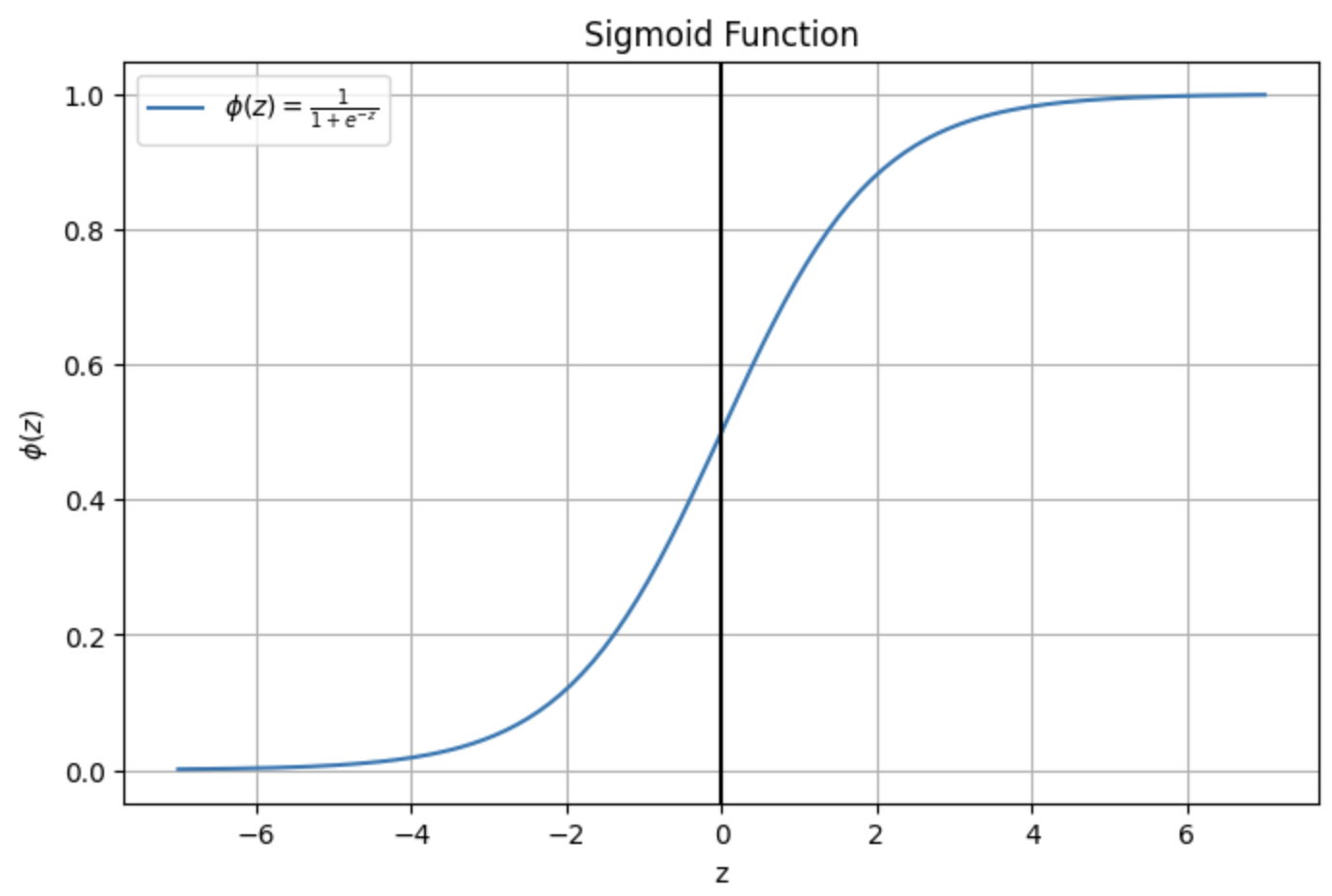
2. 次に、シグモイド関数(ロジスティック関数)で確率化
$$
\phi(z) = \frac{1}{1 + e^{-z}}
$$
シグモイド関数の出力では、データ点がクラス1に所属している確率は$\phi(z) = P(y==1 | \mathbf{x};\mathbf{w})$と書ける。たとえば、あるデータ点に対して$\phi(z) = 0.8$が算出される場合は、このデータは80%の確率でクラス1に所属していると解釈できる。
シグモイド関数は以下のような形(S字型)をしている。
コードを表示
import numpy as np
import matplotlib.pyplot as plt
# シグモイド関数の定義
def sigmoid(z):
return 1 / (1 + np.exp(-z))
# zの範囲を設定
z = np.linspace(-7, 7, 200)
# シグモイド関数の値を計算
sigma = sigmoid(z)
# グラフを描画
plt.figure(figsize=(8, 5))
plt.plot(z, sigma, label=r'$\phi(z) = \frac{1}{1 + e^{-z}}$')
plt.axvline(x=0, color='black', linewidth=1.5)
plt.title('Sigmoid Function')
plt.xlabel('z')
plt.ylabel(r'$\phi(z)$')
plt.grid(True)
plt.legend()
plt.show()
3. 最後に閾値関数を使って、確率を二値の成果指標に変換する(予測ラベルに変換)
$$
\hat{y} = \begin{cases}
1 & \phi(z) \geq 0.5 \\
0 & \phi(z) < 0.5
\end{cases}
$$
これは以下の表現でも書ける。
$$
\hat{y} = \begin{cases}
1 & z \geq 0.0 \\
0 & z < 0.0
\end{cases}
$$
2.1 ロジスティック回帰における損失関数とコスト関数
予測と実際のラベルの差を評価するのに用いるのがクロスエントロピー損失関数。このクロスエントロピー損失は、対数尤度を最大化する問題と等価であるので、1つのデータを$(x^{(i)}, y^{(i)})$とすると、
$$
\mathcal{L}(w, b; x^{(i)}, y^{(i)}) = y^{(i)} \log(\hat{y}^{(i)}) + (1 - y^{(i)}) \log(1 - \hat{y}^{(i)})
$$
ここで、$\hat{y}^{(i)} = \sigma(w^\top x^{(i)} + b)$ はシグモイド関数による予測確率である。
ロジスティック回帰では、全データに対する対数尤度の和を最大化することが目標なので、
$$
\text{maximize} \mathcal{L}(w, b; x^{(i)}, y^{(i)})
$$
ただし、一般に最適化では最小化問題に変換するため、負の対数尤度を最小化する。ゆえにコスト関数(目的関数)は、
$$
\mathcal{J}(w, b) = - \frac{1}{N} \sum_{i=1}^{N} \mathcal{L}(w, b; x^{(i)}, y^{(i)}) \\ = -\frac{1}{N} \sum_{i=1}^{N} \left[ y^{(i)} \log(\hat{y}^{(i)}) + (1 - y^{(i)}) \log(1 - \hat{y}^{(i)}) \right]
$$
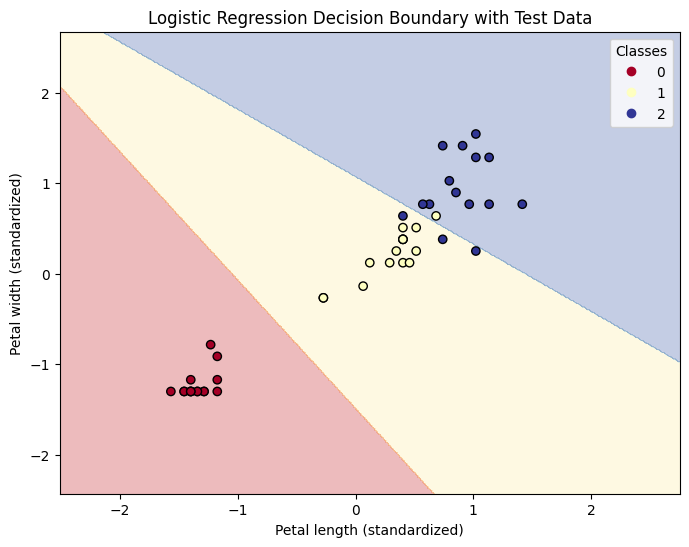
2.2 ロジスティック回帰の実装
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import numpy as np
# Irisデータセットの読み込み
# Irisデータセットは、3種類のアヤメの花の特徴を持つデータセット
iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 花弁の長さと幅
y = iris.target # 0: Setosa, 1: Versicolor, 2: Virginica
# データをトレーニング、検証、テストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# ロジスティック回帰モデルの学習 L2正則化を使用
lr_model = LogisticRegression(C=10, random_state=42, solver='lbfgs', penalty='l2')
lr_model.fit(X_train, y_train)
# テストデータでの予測
y_pred = lr_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Test Accuracy: {accuracy:.2f}")
# Test Accuracy: 0.91
# メッシュグリッドを作成して、領域全体をカバー
x_min, x_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
y_min, y_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
np.linspace(y_min, y_max, 500))
# 各グリッド点に対して予測
Z = lr_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# プロット
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
# 訓練データをプロット
scatter = plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolor='k', cmap=plt.cm.RdYlBu)
plt.xlabel('Petal length (standardized)')
plt.ylabel('Petal width (standardized)')
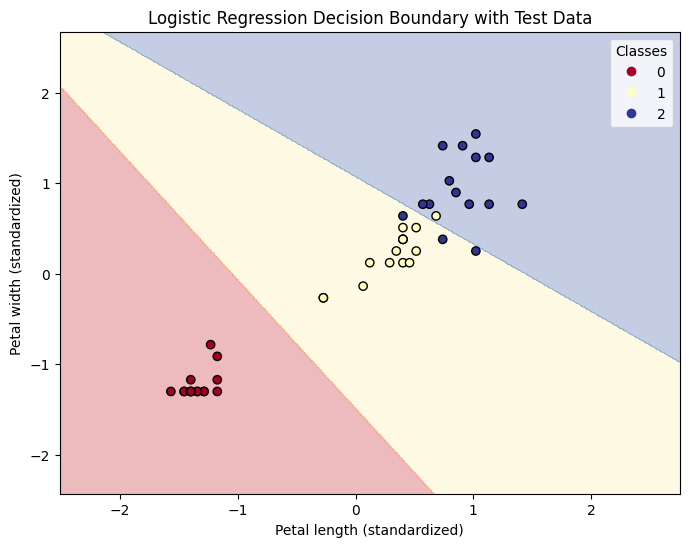
plt.title('Logistic Regression Decision Boundary with Test Data')
plt.legend(*scatter.legend_elements(), title="Classes")
plt.show()
3 サポートベクトルマシーン(SVM)
ロジスティック回帰以外の線形分類手法として、サポートベクトルマシーン(SVM)がある。この手法は超平面と呼ばれる決定境界とその超平面に最も近いデータ(サポートベクトルと呼ぶ)とのマージンを最大にするような超平面を決定する手法。
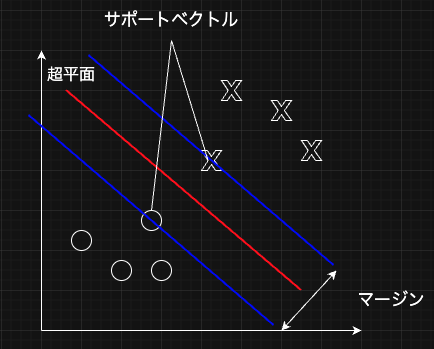
マージン$\frac{2}{||w||}$を最大化する手法であるが、その逆数をとって、2乗した$\frac{1}{2} ||w||^2$の最小化問題を目的関数とする。
3.1 ソフトマージン分類(ソフトマージンSVM)
サポートベクトルマシーンの大きな欠点として、誤分類を許容できないことがある。つまり、完全に線形分類可能な問題にしか基本的なサポートベクトルマシーンは使えない。
そこで、誤分類を許容したサポートベクトルマシーンとして登場したのが、ソフトマージン分類(ソフトマージンSVM)だ。数学的な詳細は省略するが、スラック関数$\xi$(クサイと読む)を導入することで、誤分類を含んだサポートベクトルマシーンを可能にした。ソフトマージンSVMの目的関数は以下のようになる。
$$
\min_{w, b} \quad \frac{1}{2} ||w||^2 + C \sum_{i=1}^{n} \xi_i
$$
$C$はペナルティの強さを決めるハイパーパラメータで、$C$の値が大きいと誤分類をあまり許容せず、逆に値が小さいと誤分類に関して寛大である。
3.1.1 ソフトマージンSVMの実装
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import numpy as np
# Irisデータセットの読み込み
# Irisデータセットは、3種類のアヤメの花の特徴を持つデータセット
iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 花弁の長さと幅
y = iris.target # 0: Setosa, 1: Versicolor, 2: Virginica
# データをトレーニング、検証、テストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# soft margin SVMモデルの学習
svm_model = SVC(kernel='linear', C=1.0, random_state=42)
svm_model.fit(X_train, y_train)
# テストデータでの予測
y_pred = svm_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Test Accuracy: {accuracy:.2f}")
# Test Accuracy: 0.91
# メッシュグリッドを作成して、領域全体をカバー
x_min, x_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
y_min, y_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
np.linspace(y_min, y_max, 500))
# 各グリッド点に対して予測
Z = svm_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# プロット
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
# テストデータをプロット
scatter = plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolor='k', cmap=plt.cm.RdYlBu)
plt.xlabel('Petal length (standardized)')
plt.ylabel('Petal width (standardized)')
plt.title('SVM Decision Boundary with Test Data')
plt.legend(*scatter.legend_elements(), title="Classes")
plt.show()
3.2 カーネルSVM
これまでに紹介したSVM手法では、非線形分類問題に対応できない。その解決策として、カーネル化を適応したカーネルSVMが考案された。カーネルSVMの基本的な考え方は、データを高次元空間に射影することで、線形分離できるようにすることである。
コードを表示
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 1. ばらつきのあるデータ生成
np.random.seed(42)
n = 100
r_inner = 0.3
r_outer = 0.9
# 内側と外側の半径を持つ円環状のデータを生成
theta_inner = 2 * np.pi * np.random.rand(n)
theta_outer = 2 * np.pi * np.random.rand(n)
# ノイズを加える(正規分布からの乱数)
noise_inner = 0.05 * np.random.randn(n)
noise_outer = 0.05 * np.random.randn(n)
# 内側と外側の半径にノイズを加える
r_inner_noisy = r_inner + noise_inner
r_outer_noisy = r_outer + noise_outer
# 極座標からデカルト座標に変換
X_inner = np.c_[r_inner_noisy * np.cos(theta_inner), r_inner_noisy * np.sin(theta_inner)]
X_outer = np.c_[r_outer_noisy * np.cos(theta_outer), r_outer_noisy * np.sin(theta_outer)]
# 2. 3次元へのマッピング関数
def phi(x):
return np.c_[x[:, 0], x[:, 1], x[:, 0]**2 + x[:, 1]**2]
X_mapped = phi(X)
# 3. 可視化
fig = plt.figure(figsize=(12, 5))
# 左: 元の2次元空間
ax1 = fig.add_subplot(121)
ax1.scatter(X[y==0][:,0], X[y==0][:,1], c='navy', label='Class 0', alpha=0.7, marker='^')
ax1.scatter(X[y==1][:,0], X[y==1][:,1], c='darkred', label='Class 1', alpha=0.7)
ax1.set_xlabel(r'$x_1$')
ax1.set_ylabel(r'$x_2$')
ax1.set_title("Input space (2D, with noise)")
ax1.set_aspect('equal')
ax1.legend()
# 右: 3次元空間への写像
ax2 = fig.add_subplot(122, projection='3d')
ax2.scatter(X_mapped[y==0][:,0], X_mapped[y==0][:,1], X_mapped[y==0][:,2],
c='navy', label='Class 0', alpha=0.7, marker='^')
ax2.scatter(X_mapped[y==1][:,0], X_mapped[y==1][:,1], X_mapped[y==1][:,2],
c='darkred', label='Class 1', alpha=0.7)
# 線形分離面を表示(例: z = 0.6)
x_surf, y_surf = np.meshgrid(np.linspace(-1.2, 1.2, 30), np.linspace(-1.2, 1.2, 30))
z_surf = np.full_like(x_surf, 0.6)
ax2.plot_surface(x_surf, y_surf, z_surf, alpha=0.3, color='green')
ax2.set_xlabel(r'$x_1$')
ax2.set_ylabel(r'$x_2$')
ax2.set_zlabel(r'$x_1^2 + x_2^2$')
ax2.set_title("Mapped space (3D)")
ax2.view_init(elev=10, azim=50)
ax2.legend()
plt.tight_layout()
plt.show()
これは、次の射影を使ってクラスに分類している。
$$
\phi(x_1, x_2) = (x_1, x_2, x_1^{2}+x_2^{2})
$$
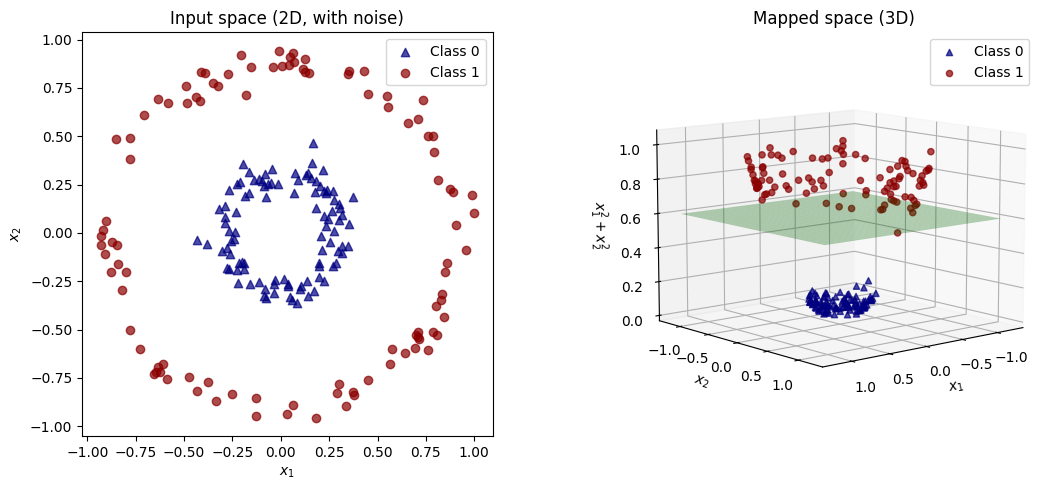
カーネルSVMは非線形のデータを高次元に射影することで、線形データの分類を可能にする。
入力ベクトル$\mathbf{x}$は$\phi : \mathbb{R}^n \rightarrow \mathbb{R}^m$を用いて、高次元空間(n次元からm次元)に射影される。
$$
x \mapsto \phi(x)
$$
しかし、もし$m$が非常に大きい、あるいは無限次元である場合、この写像を明示的に計算するのは計算コストがかかり非効率的。
実は、SVMの最適化問題や予測問題では、写像された特徴量ベクトル同士の内積が中心となるので、次の項が分かれば十分。
$$
\langle \phi(x_i), \phi(x_j) \rangle
$$
SVMの目的関数は以下のように書ける。これを見ると、写像後のベクトル自体は使わずに、写像後の内積のみが使われていることが分かる($\alpha$はラグランジュ乗数)。
$$
\max_{\alpha} \sum_i \alpha_i - \frac{1}{2} \sum_i \sum_j \alpha_i \alpha_j y_i y_j \langle \phi(x_i), \phi(x_j) \rangle
$$
ここでものを言うのが、カーネル関数を使ったカーネルトリックである。
カーネル関数にはいくつかの種類があるが、 多項式カーネルやガウスカーネル(RBFカーネル)がある。これらのカーネル関数は、データを明示的に高次元空間に写像せずとも、その写像後の内積を直接計算できる。すなわち、写像された特徴空間における内積を、元の入力ベクトルの情報だけで求めることができるため、高次元へ写像するための計算コストを大幅に削減できる。
$$
K(x_i, x_j) = \langle \phi(x_i), \phi(x_j) \rangle
$$
ここから、元の2次元特徴量ベクトルを6次元に射影する例を考える。
元の特徴ベクトル(2次元):
$$
x = \begin{bmatrix} x_1 \ x_2 \end{bmatrix}, \quad x' = \begin{bmatrix} x_1' \ x_2' \end{bmatrix}
$$
2次の多項式写像(バイアス項あり)を使うと、次のように6次元に明示的に変換できる
$$
\phi(x) = \begin{bmatrix} 1 \ \sqrt{2} x_1 \ \sqrt{2} x_2 \ x_1^2 \ x_2^2 \ \sqrt{2} x_1 x_2 \end{bmatrix}
$$
その内積を明示的に計算すると
$$
\langle \phi(x), \phi(x') \rangle = \left( 1 + x_1 x_1' + x_2 x_2' \right)^2
$$
これは、2次の多項式カーネルと一致する
$$
K(x, x') = \left( x^\top x' + 1 \right)^2
$$
つまり、元の2次元空間での計算だけで、6次元空間での内積結果が得られるため、カーネル関数を使うと計算コストが大幅に削減できる。
以下に、それぞれのカーネル関数とそのメリット、デメリット、使い所をまとめておく。
| カーネル関数 | 数式 |
|---|---|
| 線形カーネル | $$ K(x_i, x_j) = x_i^\top x_j $$ |
| 多項式カーネル | $$ K(x_i, x_j) = (x_i^\top x_j + c)^d \quad (c \geq 0, d \text{は次数}) $$ |
| ガウスカーネル(RBFカーネル) | $$ K(x_i, x_j) = \exp\left( -\frac{|x_i - x_j|^2}{2\sigma^2} \right) \quad (\sigma > 0) $$ |
| シグモイドカーネル | $$ K(x_i, x_j) = \tanh(\alpha x_i^\top x_j + c) $$ |
| ラプラシアンカーネル | $$ K(x_i, x_j) = \exp\left( -\frac{|x_i - x_j|}{\sigma} \right) $$ |
| カーネル関数 | メリット | デメリット | 使い所 |
|---|---|---|---|
| 線形カーネル | - 計算が非常に高速 - データが線形に分離可能な場合に最適 |
- 線形分離できないデータには効果が薄い | - 線形分離可能なデータセット |
| 多項式カーネル | - 高次元空間での非線形な分類が可能 - パラメータ cとdで柔軟に調整可能 |
- 高次の多項式では過学習のリスクあり - 計算量が増加する |
- 非線形だが、比較的単純な境界が必要な場合 |
| ガウスカーネル(RBFカーネル) | - 非線形の関係をうまく捉える - 高次元空間に射影することなく、非常に複雑なパターンを学習可能 |
- γの選択が非常に重要- 計算量が多くなる可能性あり |
- 複雑なデータセット、特に局所的な構造が重要な場合 |
| シグモイドカーネル | - ニューラルネットワークに似た性質を持つ - 非線形な関係に強い |
- パラメータ調整が難しい - 他のカーネルに比べて性能が劣る場合がある |
- ニューラルネットワーク的なアプローチを取りたい場合 |
| ラプラシアンカーネル | - RBFカーネルに似ており、非線形な関係をうまく捉える | - σの選択が重要- 計算量が増加する |
- 距離に基づくデータの関係を捉えたい場合 |
3.2.1 カーネルSVMの実装
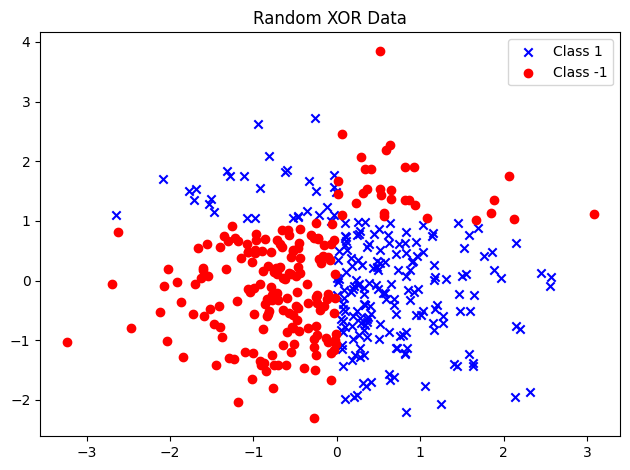
今回は非線形分類が求められるような以下のデータを作成し、カーネルSVMでの分類を試みる。
コードを表示
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# 2次元の正規分布に従うランダムなデータ点を200個生成
X_xor = np.random.randn(400, 2)
# XOR条件に基づいてラベルを作成:
# x座標が正かつ y座標が1より大きい、またはその逆(どちらか一方)のときTrue
y_xor = np.logical_xor(X_xor[:, 0] > 0, X_xor[:, 1] > 1)
# Trueを1に、Falseを-1に変換してラベルとする
y_xor = np.where(y_xor, 1, -1)
# ラベルが1のデータを青色の「×」でプロット
plt.scatter(X_xor[y_xor == 1, 0], X_xor[y_xor == 1, 1], c='b', marker='x', label='Class 1')
# ラベルが-1のデータを赤色の「〇」でプロット
plt.scatter(X_xor[y_xor == -1, 0], X_xor[y_xor == -1, 1], c='r', marker='o', label='Class -1')
# グラフを作成
plt.title('Random XOR Data')
plt.tight_layout()
plt.legend()
plt.show()
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import numpy as np
# データをトレーニング、検証、テストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X_xor, y_xor, test_size=0.3, random_state=42, stratify=y_xor)
# 標準化
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# RBF Kernel SVMモデルの学習
kernel_svm_model = SVC(kernel='rbf', random_state=42, gamma=0.1, C=10)
kernel_svm_model.fit(X_train, y_train)
# テストデータでの予測
y_pred = kernel_svm_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Test Accuracy: {accuracy:.2f}")
# Test Accuracy: 0.88
# メッシュグリッドを作成して、領域全体をカバー
x_min, x_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
y_min, y_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
np.linspace(y_min, y_max, 500))
# 各グリッド点に対して予測
Z = kernel_svm_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# プロット
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
# テストデータをプロット
scatter = plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolor='k', cmap=plt.cm.RdYlBu)
plt.xlabel('Petal length (standardized)')
plt.ylabel('Petal width (standardized)')
plt.title('Kernel SVM Decision Boundary with Test Data')
plt.legend(*scatter.legend_elements(), title="Classes")
plt.show()
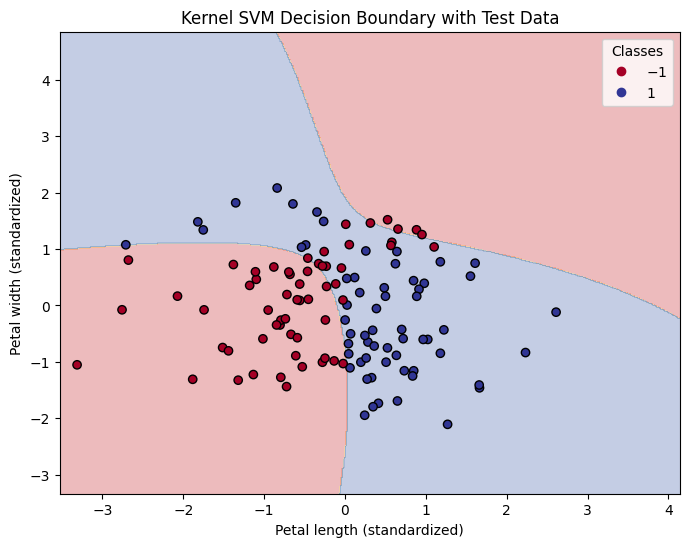
4. 決定木学習
決定木学習は意味解釈性に優れた機械学習手法である。決定木モデルは、訓練データの特徴量に基づいて、一連の条件分岐(質問)を学習し、それにより各データ点のクラスラベルを予測する。質問はカテゴリ変数に関する質問でも、連続値を持つような変数(e.g. 身長が170cm以上)でも良い。
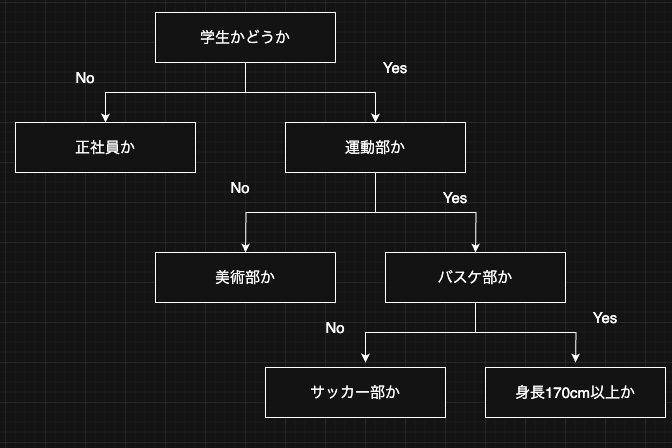
決定木の根(ルート)から始めて、各ノードではデータの純度を最も高めるような分割、すなわち情報利得(Information Gain)が最大となる特徴量でデータを分割する。 情報利得は後でより詳しく説明するが、直感的なイメージとしては、ごちゃごちゃしたデータをその特徴で上手く分けられた度合いを測る指標である。
葉が純粋になる(それぞれの葉が単一のクラスサンプルしか含まない状態)まで繰り返すことができるが、過学習に陥るので、通常は決定木の最大の深さなどに条件を設けて、決定木を剪定する。
剪定の方法には、事前剪定と事後剪定があり、事前剪定は決定木の成長をあらかじめ制限する方法(例:max_depthやmin_samples_split)であるのに対し、事後剪定は一度成長させた木を後から評価して不要な枝を削除する方法。
4.1 情報利得
決定木アルゴリズムにおける最適化は、各ノード(分割)ごとの情報利得が最大となること。この場合の目的関数は、以下のように定式化される。
$$
\mathrm{IG}(D_p, f) = I(D_p) - \sum_{j=1}^{m} \frac{N_j}{N_p} I(D_j)
$$
ここで、$f$は分割を行う特徴量、$D_p$は親のデータセット、$D_j$は$j$番目の子ノードのデータセット、 $I$は不純度を与える関数、$N_p$は親ノードのデータ点の総数、$N_j$は$j$番目の子ノードのデータ点の個数である。
このように情報利得は「親ノードの不純度」と「子ノードの不純度の合計」の差で表される。つまり、子ノードの不純度が低いほど、情報利得は大きくなる。
通常、scikit-learnを含む多くのライブラリでは、組み合わせ探索空間を減らすために、二分決定木を実装している(親ノードは2つの子ノードに分割される)ので、上式は以下のように変形できる。
$$
\mathrm{IG}(D_p, f) = I(D_p) - \frac{N_{left}}{N_p} I(D_{left}) - \frac{N_{right}}{N_p} I(D_{right})
$$
4.2 不純度
情報利得の計算には、不純度を定義する必要がある。二分決定木でよく使われる不純度の指標としてジニ不純度($I_{G}$)、エントロピー($I_{H}$)、分類誤差($I_{E}$)の3つを解説する。それぞれの指標に関して噛み砕いて説明すると、ジニ不純度はランダムに2つのサンプルを選んだとき、それらが異なるクラスになる確率、エントロピーはそのノードの情報の混乱度、誤分類(単に正しく分類できていない)割合を示す指標と考えられる。
| 指標名 | 数式 | 特徴 |
|---|---|---|
| ジニ不純度 ($I_G$) | $I_G(t) = 1 - \sum_{i=1}^{c} p(i \mid t)^2$ | - 計算が比較的簡単で、スムーズな分岐を好む - CART(Classification And Regression Tree)でよく用いられる |
| エントロピー ($I_H$) | $I_H(t) = - \sum_{i=1}^{c} p(i \mid t)\log_2 p(i \mid t)$ | - 情報理論に基づく指標。最も理論的だが、計算コストはやや高い - ID3やC4.5といった決定木アルゴリズムで用いられる。 |
| 分類誤差 ($I_E$) | $I_E(t) = 1 - \max { p(i \mid t) }$ | - 最も単純な不純度 - 直感的だが、分岐の選択にはあまり敏感でないため、剪定に使われることが多い。 |
4.3 決定木アルゴリズムの実装
決定木の大きなメリットの1つに前処理の少なさがある。決定木アルゴリズムでは、基本的に連続変数の標準化は必要なく、カテゴリ変数に関してもワンホットエンコーディングなどは必要ない。
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import numpy as np
# Irisデータセットの読み込み
# Irisデータセットは、3種類のアヤメの花の特徴を持つデータセット
iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 花弁の長さと幅
y = iris.target # 0: Setosa, 1: Versicolor, 2: Virginica
# データをトレーニング、検証、テストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
# 決定木モデルの学習
tree_model = DecisionTreeClassifier(random_state=42, max_depth=4, criterion='gini')
tree_model.fit(X_train, y_train)
# テストデータでの予測
y_pred = tree_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Test Accuracy: {accuracy:.2f}")
# Test Accuracy: 0.93
# メッシュグリッドを作成して、領域全体をカバー
x_min, x_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
y_min, y_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
np.linspace(y_min, y_max, 500))
# 各グリッド点に対して予測
Z = tree_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# プロット
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
# テストデータをプロット
scatter = plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolor='k', cmap=plt.cm.RdYlBu)
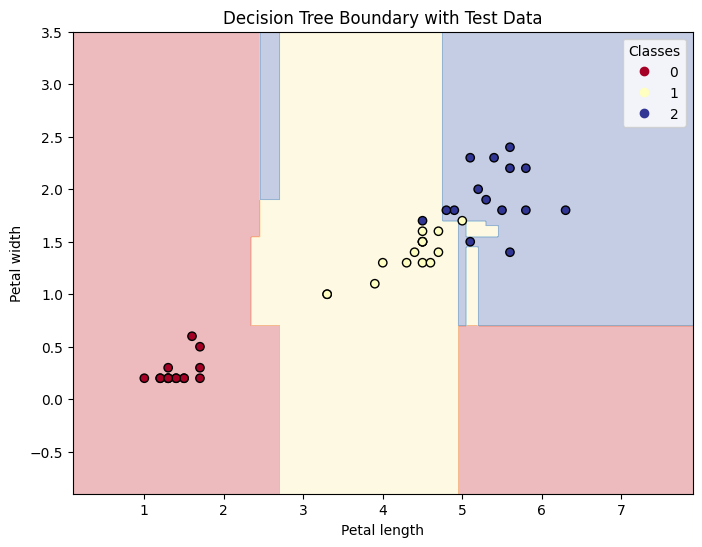
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('Decision Tree Boundary with Test Data')
plt.legend(*scatter.legend_elements(), title="Classes")
plt.show()
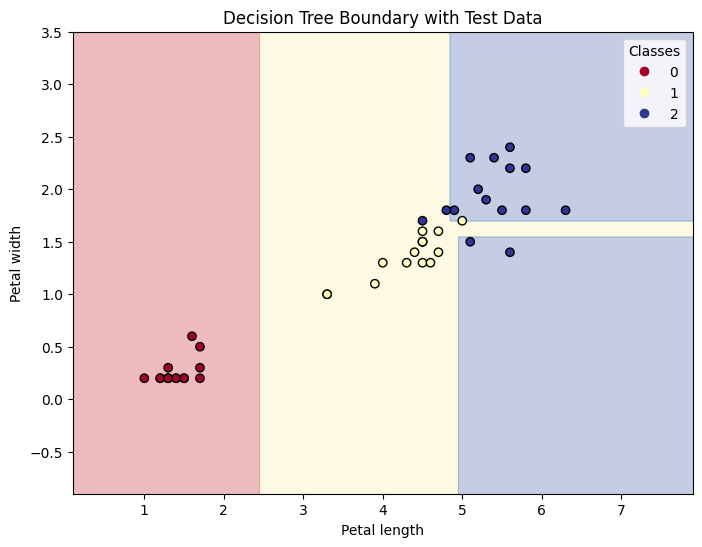
scikit-learnには、決定木を可視化する便利な機能がある。
from sklearn import tree
tree.plot_tree(tree_model, filled=True, feature_names=iris.feature_names[2:], class_names=iris.target_names)
plt.show()
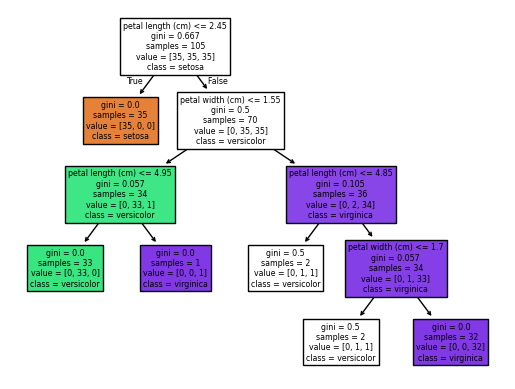
4.4 ランダムフォレスト
ランダムフォレストアルゴリズムは、決定木のアンサンブル(複数のモデルを組み合わせて予測をする手法)と見なすことができる。この手法では、バリアンスが高い複数の決定木を平均化することで、より汎用性が高く、過学習に対して堅牢なモデルを構築することを可能にしている。
ランダムフォレストは以下の4つの簡単な手順にまとめることができる。
- サイズ$n$のランダムなブーストラップ標本を復元抽出(1度取り出したサンプルを戻すことで、毎回同じデータセットから抽出)する(訓練データから$n$個のデータ点をランダムに抽出する)
- ブーストラップ標本から$d$個の特徴量をランダムに非復元抽出し、その中で目的関数に従って最適な分割となる特徴量を使ってノードを分割していく
- 手順 1~2を$k$回繰り返す
- 決定木ごとの予測をまとめ、多数決に基づいてクラスラベルを割り当てる
ランダムフォレストアルゴリズムでは、ハイパーパラメータのうち、手順3の$k$のみ自らの判断で決める必要がある。しかし、それ以外の$n$や$d$については、交差検証などのハイパーパラメータ最適化手法で最適化できる。
4.4.1 ランダムフォレストの実装
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import numpy as np
# Irisデータセットの読み込み
# Irisデータセットは、3種類のアヤメの花の特徴を持つデータセット
iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 花弁の長さと幅
y = iris.target # 0: Setosa, 1: Versicolor, 2: Virginica
# データをトレーニング、検証、テストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
# ランダムフォレストモデルの学習
forest_model = RandomForestClassifier(random_state=42, n_estimators=100, criterion='gini')
forest_model.fit(X_train, y_train)
# テストデータでの予測
y_pred = forest_model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Test Accuracy: {accuracy:.2f}")
# Test Accuracy: 0.96
# メッシュグリッドを作成して、領域全体をカバー
x_min, x_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
y_min, y_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
np.linspace(y_min, y_max, 500))
# 各グリッド点に対して予測
Z = forest_model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# プロット
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
# テストデータをプロット
scatter = plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolor='k', cmap=plt.cm.RdYlBu)
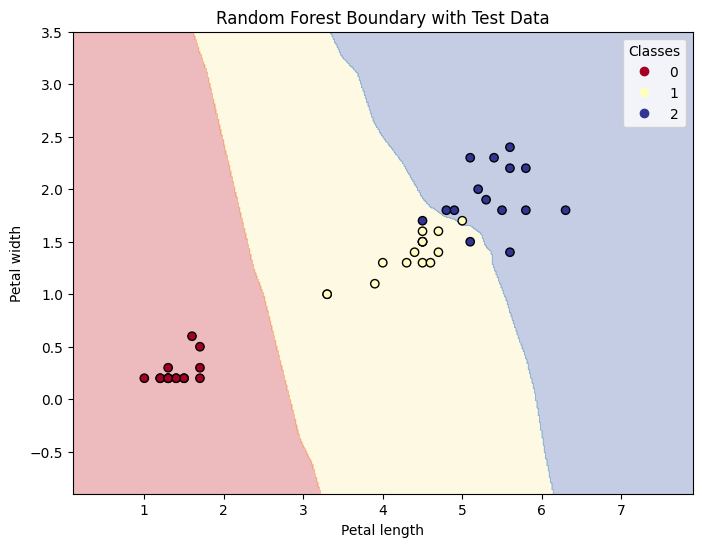
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('Random Forest Boundary with Test Data')
plt.legend(*scatter.legend_elements(), title="Classes")
plt.show()
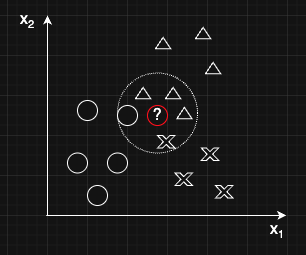
5 k最近傍法:怠惰アルゴリズム
k最近傍法(k-Nearest Neighbors: KNN)は訓練時にモデルを構築せず、予測時に全訓練データを使って計算を行う怠惰(遅延)学習(lazy learning)型のアルゴリズム。すなわち、新しいデータの予測をする際には学習は不要で、モデルではなく、訓練データそのものを保存して、予測に使う必要がある。KNNアルゴリズムそのものは非常に単純で、次の手順にまとめられる。
- $k$の値(近傍の数)と距離指標を選択する
- 分類したデータ点から$k$個の最近傍のデータ点を見つけ出す
- 多数決によりクラスラベルを割り当てる
下図は、5つの最近傍のデータ点での多数決に基づき、新しいデータ点にラベルを割り当てる様子を示している。この場合、最近傍の5個のデータのうち、三角が一番多いので、三角が割り当てられる。
KNNでは距離指標の設定も重要となる。もっとも単純な距離指標としてはユーグリッド距離が使われるが、データセットの特徴量に合わせて他の特徴量も選択することを視野に入れておく。
機械学習のモデルは大きくパラメトリックモデルとノンパラメトリックモデルに分類される。
パラメトリックモデルは、あらかじめ決まった形の関数(モデル構造)を仮定し、訓練データからその関数のパラメータ(重みなど)を推定して予測を行う。このため、学習後は固定された数のパラメータで表現され、新たなデータの予測に訓練データを保持しておく必要がない。代表例として、ロジスティック回帰や線形SVMなどがある。
一方、ノンパラメトリックモデルは、データに応じてモデルの複雑さ(自由度)を変える柔軟な構造を持つ。訓練データから明示的に固定されたパラメータを学習するのではなく、予測時にも訓練データそのものやその影響を利用することが多い。そのため、新たなデータを予測する際に訓練データを必要とするケースが多い。代表例には、決定木アルゴリズムやカーネルSVMがある。
また、ノンパラメトリックモデルの中には、インスタンスに基づく学習(Instance-Based Learning)と呼ばれる手法群が存在する。これらの手法では、明示的なモデル構造を学習せず、訓練データそのものを保持し、新たなデータの予測時に訓練データとの距離や類似度に基づいて推論を行う。典型的な例がk最近傍法である。k-NNでは、訓練時に何も学習せず、予測時に入力と最も近いk個の訓練サンプルのラベルを参照して分類や回帰を行う。このように、インスタンスベース学習はメモリ効率や予測速度に課題がある一方で、モデル構築が不要でシンプルな特性を持つ。
5.1 KNNの実装
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
import numpy as np
# Irisデータセットの読み込み
# Irisデータセットは、3種類のアヤメの花の特徴を持つデータセット
iris = datasets.load_iris()
X = iris.data[:, [2, 3]] # 花弁の長さと幅
y = iris.target # 0: Setosa, 1: Versicolor, 2: Virginica
# データをトレーニング、検証、テストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42, stratify=y)
# KNNを訓練データに適合
knn = KNeighborsClassifier(n_neighbors=5, metric='minkowski')
knn.fit(X_train, y_train)
# テストデータでの予測
y_pred = knn.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Test Accuracy: {accuracy:.2f}")
# Test Accuracy: 0.93
# メッシュグリッドを作成して、領域全体をカバー
x_min, x_max = X_train[:, 0].min() - 1, X_train[:, 0].max() + 1
y_min, y_max = X_train[:, 1].min() - 1, X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 500),
np.linspace(y_min, y_max, 500))
# 各グリッド点に対して予測
Z = knn.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# プロット
plt.figure(figsize=(8, 6))
plt.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.RdYlBu)
# テストデータをプロット
scatter = plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test, edgecolor='k', cmap=plt.cm.RdYlBu)
plt.xlabel('Petal length')
plt.ylabel('Petal width')
plt.title('Random Forest Boundary with Test Data')
plt.legend(*scatter.legend_elements(), title="Classes")
plt.show()
6 まとめ
・ロジスティック回帰:計算効率が高く、結果の解釈も比較的容易なため、二値分類問題のベースラインモデルとしてや、線形分離可能な問題に対して有効。また、確率に基づいた予測が必要な場面でも利用される。
・サポートベクトルマシーン(SVM):マージン最大化という明確な基準に基づいて決定境界を学習する手法。カーネルトリックを用いることで非線形な問題にも対応できる。高次元の特徴空間で線形分離を行うため、複雑なデータに対しても高い性能を発揮することが期待できる。ただし、パラメータ調整が難しい場合や、大規模データセットでの計算コストが課題となることがある。
・決定木学習:モデルの解釈性が非常に高く、どのような条件で分類が行われたのかを容易に理解できる。スケール変換などの前処理が不要な点もメリット。ただし、過学習しやすい傾向があるため、木の深さや葉のサンプル数などの剪定が重要になる。
・ランダムフォレスト:複数の決定木を組み合わせたアンサンブル学習アルゴリズムです。各決定木は異なるデータや特徴量のサブセットで学習されるため、個々の決定木の欠点を補い合い、汎化性能の高いモデルを構築できる。決定木と比較して過学習しにくく、多くの実用的な問題で優れた性能を発揮する。
・k-最近傍法(KNN):予測したいデータの近くにあるk個の訓練データのクラスラベルに基づいて分類を行う、インスタンスベース学習の手法。モデルの学習が不要で実装が容易である一方、予測時に全ての訓練データとの距離を計算する必要があるため、大規模データセットでは計算コストが高くなる。また、適切なkの値や距離指標の選択が性能に大きく影響する。
また、本記事では分類問題のみを扱ったが、ロジスティック回帰以外の手法は回帰問題にも適用可能である。