機械学習モデルの精度を大きく左右する「前処理」。
本記事では、前処理の基礎から実践までを体系的に解説します。
扱う内容は、欠損値の処理、カテゴリ変数のエンコーディング、特徴量のスケーリング、そして特徴量選択まで。どれも実際のプロジェクトで避けては通れない重要なステップです。
すべての処理にはPythonによる実装コードを添えているため、理論だけでなく実践的なスキルも身につきます。
本記事は、名著Python機械学習プログラミング 達人データサイエンティストによる理論と実践第4章をベースに、自身の理解を深めながらまとめた内容です。
これから機械学習に取り組む方、あるいは前処理を整理して学び直したい方にとって、実用的なリファレンスになることを目指しています。
本記事では以下の流れで説明する。
Python version: 3.10.4
numpy version: 2.2.5
matplotlib version: 3.10.1
scikit-learn version: 1.6.1
pandas version: 2.2.3
mlxtend version: 0.23.4
1 欠損値データへの対処
データ分析において欠損値の処理はマスト。欠損値への対処は主に以下の2つ。
1. 欠損値を持つデータを削除する
1. 欠損値を補完する
本節では以下のデータを使って、欠損値の処理について説明する。
コードを表示
import pandas as pd
import numpy as np
np.random.seed(42)
# まずリストとして値を作成
values = list(np.random.randint(1, 10, size=10))
values.extend([np.nan] * 2) # NaN を追加
np.random.shuffle(values) # リストをシャッフル
data = np.array(values).reshape(3, 4)
df = pd.DataFrame(data, columns=['A', 'B', 'C', 'D'])
| A | B | C | D |
|---|---|---|---|
| NaN | 5.0 | 7.0 | 5.0 |
| 7.0 | 4.0 | 7.0 | 3.0 |
| 8.0 | 8.0 | NaN | 5.0 |
1.1 欠損値を特定する
データの前処理として、まず欠損値の有無を確認する必要がある。Pandasでは、is.null() も is.na()も同じ機能を果たす。
# 各列に欠損値がいくつあるか数える
df.isnull().sum()
# データ全体で欠損値がいくつあるか
total_missing = df.isna().sum().sum()
print(total_missing)
# 2
| 列名 | 欠損数 |
|---|---|
| A | 1 |
| B | 0 |
| C | 1 |
| D | 0 |
1.2 欠損値をもつデータを削除する
# NaNを含む行を削除
df.dropna(axis=0)
| A | B | C | D |
|---|---|---|---|
| 7.0 | 5.0 | 4.0 | 7.0 |
# NaNを含む列を削除
df.dropna(axis=1)
| B | D |
|---|---|
| 4.0 | 5.0 |
| 5.0 | 7.0 |
| 8.0 | 8.0 |
# 全ての列がNaNの行を削除
df.dropna(how='all')
| A | B | C | D |
|---|---|---|---|
| NaN | 5.0 | 7.0 | 5.0 |
| 7.0 | 4.0 | 7.0 | 3.0 |
| 8.0 | 8.0 | NaN | 5.0 |
1.3 欠損値を補完する
一部の列に欠損値があるだけで、貴重なデータを失いたくない時は欠損値を補完する方法を取る。補完する方法は様々あるが、この例では平均値を使って補完する(平均値補完)。
# scikit-learnのImputerを使う
from sklearn.impute import SimpleImputer
imr = SimpleImputer(missing_values=np.nan, strategy='mean')
imr = imr.fit(df.values)
imputed_data = imr.transform(df.values)
print(imputed_data)
[[5. 4. 7. 5. ]
[7. 5. 4. 7. ]
[3. 8. 5.5 8. ]]
# pandasのfillnaを使う
df.fillna(df.mean(), inplace=True)
print(df)
| A | B | C | D |
|---|---|---|---|
| 5.0 | 4.0 | 7.0 | 5.0 |
| 7.0 | 5.0 | 4.0 | 7.0 |
| 3.0 | 8.0 | 5.5 | 8.0 |
2 カテゴリデータの処理
カテゴリデータには順序特徴量と名義特徴量がある。順序特徴量は服のサイズのように並べ替えや順序付けが可能なカテゴリ量。名義特徴量は色などの順序のない特徴量。
本節では以下のカテゴリデータを含んだデータを用いる。
コードを表示
import pandas as pd
df = pd.DataFrame([
['green', 'M', 10.1, 'class2'],
['red', 'L', 13.5, 'class1'],
['blue', 'XL', 15.3, 'class2']])
df.columns = ['color', 'size', 'price', 'classlabel']
print(df)
| color | size | price | classlabel |
|---|---|---|---|
| green | M | 10.1 | class2 |
| red | L | 13.5 | class1 |
| blue | XL | 15.3 | class2 |
2.1 順序特徴量のマッピング
順序特徴量の順序や大小関係を、自動的に判別して文字列を整数に変更してくれるアルゴリズムは存在しない。そのため、手動で変換マッピングを定義する必要がある。
サイズに関する特徴量で$XL = L+1 = M+2$のような差があるとすると
# Tシャツのサイズと整数値を対応させる辞書を作成
size_mapping = {'XL': 3, 'L': 2, 'M': 1}
# サイズを数値に変換
df['size'] = df['size'].map(size_mapping)
print(df)
# 変換後の数値をカテゴリ値に戻す
# inv_size_mapping = {v: k for k, v in size_mapping.items()}
# df['size'] = df['size'].map(inv_size_mapping)
| color | size | price | classlabel |
|---|---|---|---|
| green | 1 | 10.1 | class2 |
| red | 2 | 13.5 | class1 |
| blue | 3 | 15.3 | class2 |
2.2 クラスラベルのエンコーディング
多くのscikit-learnのライブラリは内部でカテゴリ変数を自動で整数に変換してくれる。しかし、技術的なミスを避けるためにも、あらかじめクラスラベルの変換をしておくのがベストプラクティス。
2.2.1 データ内に2つのラベルしか含まない名義特徴量
マッピングディクショナリを使った方法
class_mapping = {label: idx for idx, label in enumerate(np.unique(df['classlabel']))}
df['classlabel'] = df['classlabel'].map(class_mapping)
print(df)
# 変換後の数値をカテゴリ値に戻す
# inv_class_mapping = {v: k for k, v in class_mapping.items()}
# df['classlabel'] = df['classlabel'].map(inv_class_mapping)
| color | size | price | classlabel |
|---|---|---|---|
| green | M | 10.1 | 1 |
| red | L | 13.5 | 0 |
| blue | XL | 15.3 | 1 |
scikit-learnにあるLabelEncoderを使う方法
from sklearn.preprocessing import LabelEncoder
# LabelEncoderのインスタンスを作成
class_le = LabelEncoder()
# fitメソッドでクラスラベルを学習
y = class_le.fit_transform(df['classlabel'].values)
df['classlabel'] = y
print(df)
# 変換後の数値をカテゴリ値に戻す
# df['classlabel'] = class_le.inverse_transform(df['classlabel'])
| color | size | price | classlabel |
|---|---|---|---|
| green | M | 10.1 | 1 |
| red | L | 13.5 | 0 |
| blue | XL | 15.3 | 1 |
2.2.2 データ内に3以上のラベルを含む名義特徴量(one-hotエンコーディング)
3つ以上のラベルを含む特徴量をLabelEncoderを使って変換すると、以下のようになる。
・green -> 0
・red -> 1
・blue -> 2
このような変換をしてしまうと、学習アルゴリズムはredがgreenよりも大きく、blueがredよりも大きいと認識をしてします。そのため、3つ以上のラベルを含むカテゴリ変数はone-hotエンコーディングを使って変換する。この手法は、名義特徴量の一意な値ごとにダミー特徴量を新たに作成する。
OneHotEncoderを使った場合
from sklearn.preprocessing import OneHotEncoder
# OneHotEncoderのインスタンスを作成
color_ohe = OneHotEncoder()
# one-hotエンコーディングを実行
color_onehot = color_ohe.fit_transform(df[['color']])
# one-hotエンコーディングの結果をDataFrameに変換
color_onehot_df = pd.DataFrame(color_onehot.toarray(), columns=color_ohe.get_feature_names_out(['color']))
# 元のDataFrameと結合
df_onehot1 = pd.concat([df, color_onehot_df], axis=1)
print(df_onehot1)
| size | price | classlabel | color_blue | color_green | color_red |
|---|---|---|---|---|---|
| M | 10.1 | class2 | 0 | 1 | 0 |
| L | 13.5 | class1 | 0 | 0 | 1 |
| XL | 15.3 | class2 | 1 | 0 | 0 |
pandasのget_dummies関数を使った場合
df_onehot2 = pd.get_dummies(df, columns=['color'], prefix='color')
print(df_onehot2)
ここで注意。全てのラベルをダミー変数に変換して、モデルに利用してしまうと多重共線性(変数間の相関が高すぎること)が発生する。これを防ぐためにone-hotエンコーディングの配列から特徴量ダミーを1つ削除する必要がある。ただし、特徴量ダミーを削除しても情報が失われないように注意する。今回の場合、color_redダミーを削除しても、color_blueとcolor_greenダミーが0の時、redであることを意味していると自ずと分かるため、ダミー変数を1つ削除しても問題ない。
よって、実務では以下のようなコードでone-hotエンコーディングを実施する。
OneHotEncoderを使った場合
# OneHotEncoderのインスタンスを作成
color_ohe = OneHotEncoder(drop='first')
# one-hotエンコーディングを実行
color_onehot = color_ohe.fit_transform(df[['color']])
# one-hotエンコーディングの結果をDataFrameに変換
color_onehot_df = pd.DataFrame(color_onehot.toarray(), columns=color_ohe.get_feature_names_out(['color']))
# 元のDataFrameと結合
df_onehot4 = pd.concat([df, color_onehot_df], axis=1)
# 元のDataFrameのcolor列を削除
df_onehot4.drop('color', axis=1, inplace=True)
print(df_onehot4)
| size | price | classlabel | color_green | color_red |
|---|---|---|---|---|
| M | 10.1 | class2 | True | False |
| L | 13.5 | class1 | False | True |
| XL | 15.3 | class2 | False | False |
pandasのget_dummies関数を使った場合
# 多重共線性を回避するために、ダミー変数の1つを削除
df_onehot3 = pd.get_dummies(df, columns=['color'], prefix='color', drop_first=True)
print(df_onehot3)
| size | price | classlabel | color_green | color_red |
|---|---|---|---|---|
| M | 10.1 | class2 | True | False |
| L | 13.5 | class1 | False | True |
| XL | 15.3 | class2 | False | False |
3 特徴量スケーリング
特徴量のスケーリングを揃える必要がある。ただし、特徴量スケーリングが必要ない機械学習アルゴリズムも一部ある(e.g. 決定木ベースの手法)。例えば、2つの特徴量があり、特徴量Aは1~10、特徴量Bは1~100万とかのスケーリングで計測されているとする。このままだと、アルゴリズムはより大きな誤差を生み出す特徴量Bに従って重みを最適化してしまう。また、データ間の距離を学習するアルゴリズム(e.g. KNN)でもスケールの大きい特徴量Bが支配的な振る舞いをしてしまう。
複数の特徴量を揃える手法として、正規化(normalization)と標準化(standardization)の2つがある。これらの言葉は分野によっては曖昧に使われるので注意する。
正規化では、特徴量を[0, 1]の範囲にスケーリングする。これはmin-maxスケーリングと同じ操作を指す。
$$
x_{norm}^{(i)} = \frac{x^{(i)} - x_{\min}}{x_{\max} - x_{\min}}
$$
$x_{\min}$、$x_{\max}$は各特徴量の列における最小値と最大値である。
今回の演習ではUCI Machine Learning RepositoryのWineデータセットを使う。
コードを表示
# UCI Machine Learning RepositoryからWineデータセットを取得
df_wine = pd.read_csv('https://archive.ics.uci.edu/'
'ml/machine-learning-databases/wine/wine.data',
header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
'Color intensity', 'Hue', 'OD280/OD315 of diluted wines',
'Proline']
print('Class labels', np.unique(df_wine['Class label']))
# Class labels [1 2 3]
先頭の5行を表示
df_wine.head().iloc[:, :5]
データを表示
| Class label | Alcohol | Malic acid | Ash | Alcalinity of ash |
|---|---|---|---|---|
| 1 | 14.23 | 1.71 | 2.43 | 15.6 |
| 1 | 13.20 | 1.78 | 2.14 | 11.2 |
| 1 | 13.16 | 2.36 | 2.67 | 18.6 |
| 1 | 14.37 | 1.95 | 2.50 | 16.8 |
| 1 | 13.24 | 2.59 | 2.87 | 21.0 |
このデータに対して、正規化を実行する。
from sklearn.preprocessing import MinMaxScaler
# MinMaxScalerのインスタンスを作成
mms = MinMaxScaler()
# 訓練データをスケーリング
X_train_scaled = mms.fit_transform(X_train)
# テストデータをスケーリング
X_test_scaled = mms.transform(X_test)
## 正規化が適切に実行されたか確認する。各特徴量が[0, 1]になっていることを確認。
# 各列の最小値と最大値を確認(行方向=axis=0)
# print("訓練データのスケーリング後の最小値(各特徴量ごと):")
# print(np.min(X_train_scaled, axis=0))
# print("訓練データのスケーリング後の最大値(各特徴量ごと):")
# print(np.max(X_train_scaled, axis=0))
# もしくはdescribe関数を使う
# pd.DataFrame(X_train_scaled).describe()
正規化(min-maxスケーリング)よりも機械学習アルゴリズムには標準化の方が実用的である。なぜなら、多くの線形モデルが重みを0や0に近い乱数に初期化するから。標準化は特徴量を平均0、標準偏差1に変換する。これにより、特徴量の各列が標準の正規分布に従うため、重みを学習しやすくなる。
さらに、標準化だと外れ値に関する情報もある程度維持される(正規化は外れ値が基準となっているため、他の値との相対的な距離が縮まり、外れ値の異常さが目立たなくなるため)。
$$
x_{std}^{(i)} = \frac{x^{(i)} - {\mu_x}}{\sigma_x}
$$
上述の正規化と同じデータ(UCI Machine Learning RepositoryのWineデータセット)を使って、標準化の例を見る。
from sklearn.preprocessing import StandardScaler
# StandardScalerのインスタンスを作成
ss = StandardScaler()
# 訓練データをスケーリング
X_train_scaled = ss.fit_transform(X_train)
# テストデータをスケーリング
X_test_scaled = ss.transform(X_test)
## 標準化が適切に実行されたか確認する。各特徴量の平均が0、標準偏差が1になっていることを確認
# 各列の平均と標準偏差を確認(行方向=axis=0)
# print("訓練データのスケーリング後の平均(各特徴量ごと):")
# print(np.mean(X_train_scaled, axis=0))
# print("訓練データのスケーリング後の標準偏差(各特徴量ごと):")
# print(np.std(X_train_scaled, axis=0))
他のスケーリング手法として、RobustScalerなどがある。RobustScalerは第1四分位数と第3四分位数に従ったスケーリングと中央値の削除を行う。これにより、極端な値や外れ値が目立たなくなるので、多くの外れ値が含んでいるデータのスケーリングに有効である。
4 逐次特徴量選択アルゴリズム
モデルの複雑さを低減して、過学習を回避する方法として次元削減がある。この方法は特に正則化されていないアルゴリズムに役立つ。次元削減の手法は主に以下の2つに分けられる。
・特徴量選択:元の特徴量の一部を選択する。
・特徴量抽出:元の特徴量から情報を抽出して、新しい特徴量部分空間を作る。
本記事では、特徴量選択のみ解説する。特徴量抽出に関しては、次の記事(次元削減)にて説明する。
逐次特徴量アルゴリズムは貪欲探索(greedy search)の1種。貪欲探索アルゴリズムでは元々の特徴量空間の次元(d次元)をk次元に削減するために使われる(d > k)。
特徴量選択の目的は主に以下の2つ。
・計算効率を改善(問題に最も関連のある特徴量を厳選することにより)
・モデルの汎化誤差を削減(無関係の特徴量やノイズの取り除くことで)
補足
貪欲探索法では、組み合わせ探索の各段階で局所的に最適解が得られ、準最適解が得られる。これに対して、しらみつぶし探索法(exhaustive search algorithm)では考える全ての組み合わせが評価された後、最適解が得られる。大抵の場合、しらみつぶし探索法は計算量の観点で実行不可である。
特徴量選択の手法は3つのカテゴリーに分けられる。それぞれの名称と特徴を以下の表に記載してある。
・フィルター法:個々の特徴量と目的関数の統計的関係が低い特徴量を削除する。
・ラッパー法:特徴量の全ての組み合わせについてモデルを訓練し、最も性能が良かった特徴量の組み合わせを採用する手法
・埋め込み法:LightGBMのようなモデル自体が各特徴量の重要度を評価するモデルと一緒に使われる。
| 名称 | フィルター法(Filter) | ラッパー法(Wrapper) | 埋め込み法(Embedded) |
|---|---|---|---|
| 特徴量評価のタイミング | モデル学習の前 | モデル学習と切り離して特徴量を評価 | モデル学習と同時に特徴量を選択 |
| 基準 | 統計的指標(相関、情報量など) | モデル性能(精度、損失など) | モデルの内部構造や正則化による重要度 |
| 計算コスト | 低 | 高 | 中〜高(モデルに依存) |
| モデル依存性 | なし(汎用的) | あり(特定のモデルで評価) | あり(特定のモデルに組み込まれる) |
| 精度 | やや低め(単純な指標での評価) | 高い(モデルに最適な特徴量を選ぶ) | 高い(モデルに適合しやすい) |
| 例 | - 分散しきい値 - 相関係数 - カイ二乗検定 - 相互情報量 |
- Forward Selection - Backward Selection - RFE |
- Lasso(L1) - Decision Tree - XGBoost |
| 利点 | - 計算が速い - 高次元にも対応しやすい |
- 高精度が期待できる - 特徴量の組み合わせを考慮 |
- 正則化やツリーベースで自然に重要度を得られる |
| 欠点 | - モデル性能と直結しない - 組み合わせを無視 |
- 計算負荷が高い - 過学習リスクあり |
- 特定のモデルに依存 - 柔軟性がやや低い |
ここでは、ラッパー法の逐次後退選択(Sequential Backward Selection:SBS)を使って演習を行う。SBSは以下のステップで行われる。
- 全ての特徴量を使ってモデルを作成
- 1つずつ特徴量を除外して、その都度モデルの性能を評価
- 最も性能の低下が低い特徴量を除外(目的変数の予想に関係が少ない特徴量を削除)
- 目的の特徴量数になるまで繰り返す
from mlxtend.feature_selection import SequentialFeatureSelector as SBS
from sklearn.linear_model import LogisticRegression
# ロジスティック回帰モデルのインスタンスを作成
model = LogisticRegression(solver='liblinear', random_state=42)
# SFSのインスタンスを作成
sbs = SBS(estimator=model, # モデルを指定
k_features=3, # 選択する特徴量の数
forward=False, # 後向き選択
floating=False, # 浮動選択
scoring='accuracy', # 評価指標
cv=0) # クロスバリデーションの分割数
# 標準化されたUCI Wineデータセットの訓練データを使用
sbs.fit(X_train_scaled, y_train)
# 選択された特徴量のインデックスを取得
selected_features = sbs.k_feature_idx_
print('選択された特徴量のインデックス:', selected_features)
# 選択された特徴量のインデックス: (0, 2, 10)
# 選択された特徴量の名前を取得
feature_names = df_wine.columns[1:]
print('選択された特徴量の名前:', feature_names[list(selected_features)])
# 選択された特徴量の名前: Index(['Alcohol', 'Ash', 'Hue'], dtype='object')
今回は3つの特徴量を用いて新たなモデルを構築した。
以下に、特徴量の数と訓練データにおける正解率の関係性を表すグラフを示す。
コードを表示
import matplotlib.pyplot as plt
# 特徴量の個数を取得
k_feat = [k for k in list(sbs.subsets_)]
print('選択された特徴量の数:', k_feat)
# 選択された特徴量の数: [13, 12, 11, 10, 9, 8, 7, 6, 5, 4, 3]
# 横軸を選択された特徴量の数、縦軸を正解率にしてプロット
plt.plot(k_feat, [sbs.subsets_[k]['avg_score'] for k in k_feat], marker='o')
plt.xlabel('Number of features')
plt.ylabel('Accuracy')
plt.title('SBS: Sequential Backward Selection')
plt.grid()
plt.show()
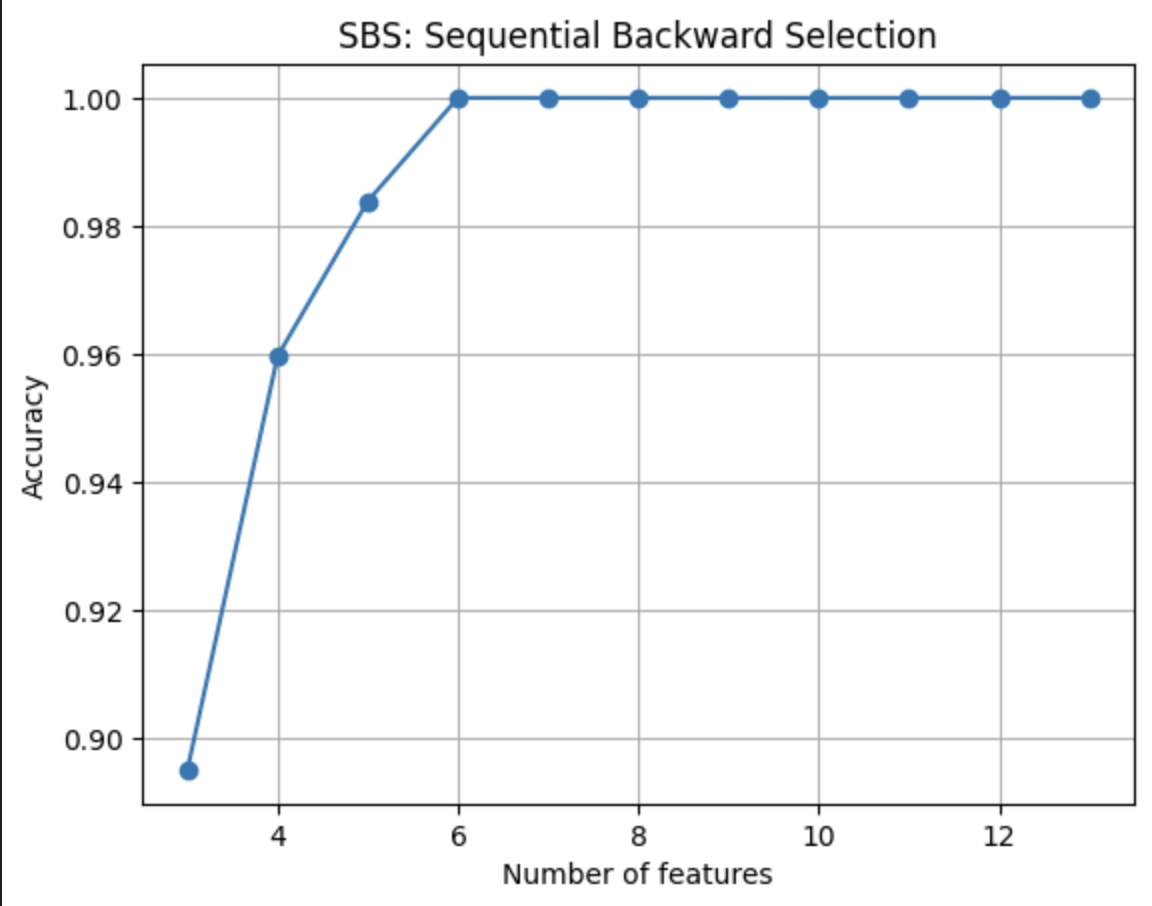
最後に、全ての特徴量(13個)を使ったモデルと、SBSにより選択された3つの特徴量を用いて構築モデルを使用し、テストデータに対する正解率を比較する。
コードを表示
# 全ての特徴量を使ったモデルの正解率
model.fit(X_train_scaled, y_train)
accuracy = model.score(X_test_scaled, y_test)
print('全ての特徴量を使ったモデルの正解率:', accuracy)
# sbsで選ばれた3つの特徴量を使った場合
model.fit(X_train_scaled[:, list(selected_features)], y_train)
accuracy = model.score(X_test_scaled[:, list(selected_features)], y_test)
print('選ばれた3つの特徴量を使ったモデルの正解率:', accuracy)
全ての特徴量を使ったモデルの正解率: 0.9814814814814815
選ばれた3つの特徴量を使ったモデルの正解率: 0.9259259259259259
今回の例では、特徴量の個数を減らしても予測精度は向上しなかった。しかし、少なくともモデルの解釈は容易になった。今回の結果から、アルコール度数(Alcohol)・灰分(Ash)・色相(Hue)の3つの特徴量で十分ワインの種類を分類することができると考えられる。
5 ランダムフォレストで特徴量の重要度を評価する
4節で解説した方法以外にもランダムフォレスト(RF)を使って、特徴量選択を行う方法もある。RF内での全ての決定木から計算された不純度の平均的な減少量を用いて、特徴量の重要度を計算する。RFにおいては、不純度を大きく減らす特徴量ほど、重要な特徴量とみなされる。直感的には、モデルがよく使っている特徴量ほど重要とみなす。
from sklearn.ensemble import RandomForestClassifier
# ランダムフォレストのインスタンスを作成
rf = RandomForestClassifier(n_estimators=100, random_state=42)
# ランダムフォレストを訓練
rf.fit(X_train_scaled, y_train)
# 特徴量の重要度を取得
importances = rf.feature_importances_
# 重要度の降順で特徴量のインデックスを取得
indices = np.argsort(importances)[::-1]
# 特徴量の名称を取得
feature_names = df_wine.columns[1:]
# 特徴量の重要度を表示
for f in range(X_train.shape[1]):
print(f"{f + 1:2d}. {feature_names[indices[f]]} ({importances[indices[f]]:.3f})")
# 1. Color intensity (0.180)
# 2. Flavanoids (0.166)
# 3. Alcohol (0.142)
# 4. Proline (0.126)
# 5. OD280/OD315 of diluted wines (0.096)
# 6. Hue (0.086)
# 7. Total phenols (0.060)
# 8. Magnesium (0.035)
# 9. Alcalinity of ash (0.033)
# 10. Proanthocyanins (0.030)
# 11. Malic acid (0.029)
# 12. Ash (0.012)
# 13. Nonflavanoid phenols (0.005)
plt.figure(figsize=(10, 6))
plt.title('Feature Importances')
plt.bar(range(X_train.shape[1]), importances[indices], align='center')
plt.xticks(range(X_train.shape[1]), feature_names[indices], rotation=90)
plt.xlim([-1, X_train.shape[1]])
plt.tight_layout()
plt.show()
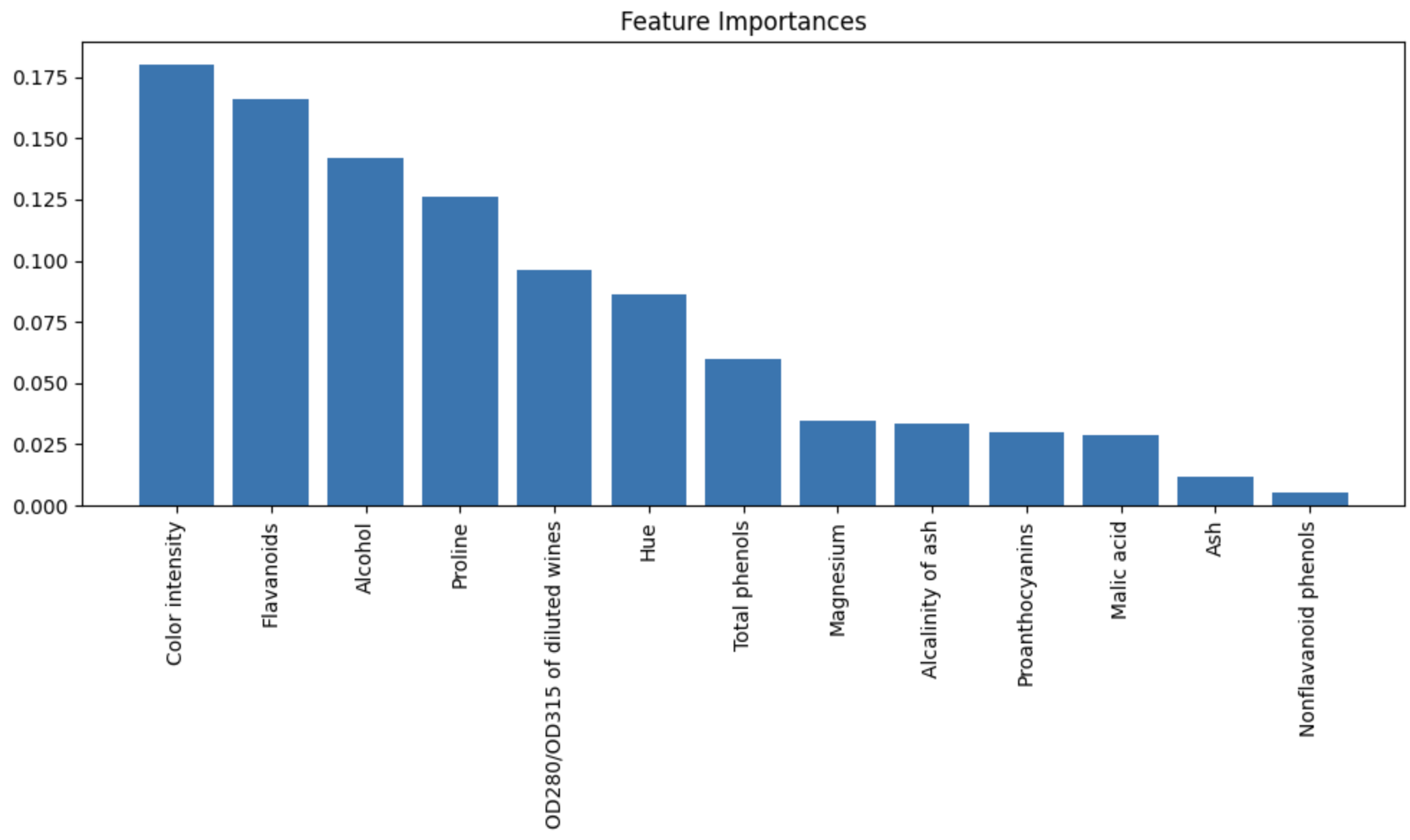
この手法では、重要度は合計が1になるように正規化されている。
sklearn内のSelectFromModelクラスの実装も行う。このクラスは、モデルを適合させた後にユーザーが指定した閾値以上の重要度をもつ特徴量を選択することができる。
from sklearn.feature_selection import SelectFromModel
# SelectFromModelのインスタンスを作成
sfm = SelectFromModel(rf, threshold=0.1, prefit=True)
# 特徴量の選択
X_important = sfm.transform(X_train_scaled)
# 選択された特徴量のインデックスを取得
selected_features = sfm.get_support(indices=True)
print('選択された特徴量のインデックス:', selected_features)
# 選択された特徴量の名前を取得
feature_names = df_wine.columns[1:]
print('選択された特徴量の名前:', feature_names[selected_features])
for i, idx in enumerate(selected_features):
print(f"{i + 1:2d}. {feature_names[idx]} ({importances[idx]:.3f})")
# 選択された特徴量のインデックス: [ 0 6 9 12]
# 選択された特徴量の名前: Index(['Alcohol', 'Flavanoids', 'Color intensity', 'Proline'], dtype='object')
# 1. Alcohol (0.142)
# 2. Flavanoids (0.166)
# 3. Color intensity (0.180)
# 4. Proline (0.126)
RFによる特徴量選択においては、意味解釈に注意する必要がある。2つ以上の特徴量の相関が高い場合、1つの特徴量のランクは非常に高いものの、残りの特徴量のランクの重要度はランクに十分に反映されていない可能性がある。
RFは不純度の減少量の大きさで、特徴量の重要度を評価している。このため、例えば$x1$と$x2$の相関が高い場合は以下のような現象が起こる。
- 決定木はランダムに特徴量を選んで分割を試みる
- $x1$と$x2$はほとんど同じ情報を持っているので、どちらか1つが使われれば、もう片方はあまり使われなくなる
- 結果として、たとえ$x2$が実際には重要でも、木では$x1$の方がよく使われた場合、
- $x1$のジニ重要度は高くなる
- $x2$のジニ重要度は低くなってしまう
この問題の解決策として、順列重要度(Permutation Importance)を使用する方法がある。
5.1 順列重要度
順列重要度は、学習済みモデルに対して、各特徴量の相対的な重要性を評価する手法。特徴量を一つずつシャッフルして、モデルの性能がどれだけ悪化するかを見ることで、その特徴量がどれほど重要だったかを判断する。
- モデルを学習済みにしておく
- 1つの特徴量を選択して、その値をシャッフルする(それぞれのデータのAlcoholの値をシャッフルしてあべこべにする)
- そのシャッフルしたデータを使って予測(予測精度が下がるなら、その特徴量は重要だったと言える)
- これをすべての特徴量に対して繰り返す( 精度の下がり幅が大きい特徴量ほど重要だと判断される)
この方法のメリットとして、以下がある。
- モデルに依存しない(決定木・SVM・ロジスティック回帰などどんなモデルでも使える)
- 相関の影響が少ない(ランダムフォレストのように1つの特徴量に重要度が偏らない)
- 解釈しやすい(性能が下がる=重要という直感的な意味を持つ)
以下は注意点。
- 計算コストが高い(各特徴量について何度もシャッフル・予測するため処理時間がかかる)
- ノイズに弱い(モデル性能が元々低いと、精度の変化も小さくなり重要度が分かりにくい)
- データリークに注意(テストデータや検証データで評価するのが鉄則。訓練データでやると過学習の影響)
from sklearn.linear_model import LogisticRegression
from sklearn.inspection import permutation_importance
# ロジスティック回帰モデルのインスタンスを作成
model = LogisticRegression(solver='liblinear', random_state=42)
# 標準化されたUCI Wineデータセットの訓練データを使用
model.fit(X_train_scaled, y_train)
# 順列重要度の計算
result = permutation_importance(model, X_test_scaled, y_test, n_repeats=30, scoring='accuracy', random_state=42)
# 結果を表示
importance_df = pd.DataFrame({
'feature': df_wine.columns[1:],
'importance_mean': result.importances_mean,
'importance_std': result.importances_std
}).sort_values(by='importance_mean', ascending=False)
print(importance_df)
# feature importance_mean importance_std
# 6 Flavanoids 0.085802 0.024606
# 9 Color intensity 0.069753 0.024232
# 12 Proline 0.057407 0.024544
# 0 Alcohol 0.055556 0.023907
# 4 Magnesium 0.011111 0.009072
# 1 Malic acid 0.000000 0.000000
# 2 Ash 0.000000 0.000000
# 3 Alcalinity of ash 0.000000 0.000000
# 5 Total phenols 0.000000 0.000000
# 7 Nonflavanoid phenols 0.000000 0.000000
# 8 Proanthocyanins 0.000000 0.000000
# 10 Hue 0.000000 0.000000
# 11 OD280/OD315 of diluted wines 0.000000 0.000000
ランダムフォレストで得られた重要度と、順列重要度で得られた重要度のランクでは少し違いがある。