はじめに
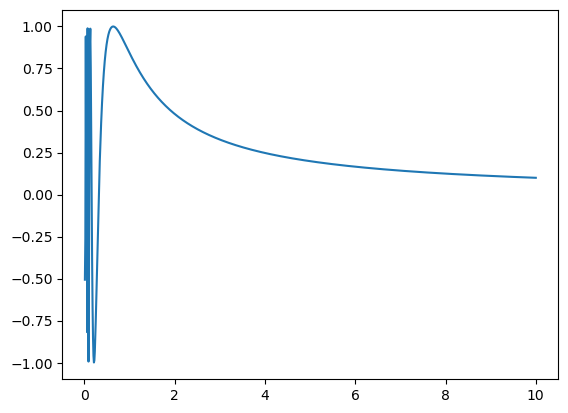
$y = \sin(1/x)$という関数を考えてみましょう。そして、この関数の積分について考えてみます。これだけシンプルな関数ならば、解析的に解くにせよ、プログラムで数値的に解くにせよ難しくないように思えます。しかし、これが一筋縄ではいかないのです。
解析的に解く場合、これはきれいに解けません。そして、数値的に解く場合でも、実はきれいに解けないのです。なぜでしょう。
$y = \sin(1/x)$のグラフを見てみましょう。
import numpy as np
import matplotlib.pyplot as plt
f = lambda x: np.sin(1 / x)
x = np.linspace(0.01, 10, 1000)
y = f(x)
plt.plot(x, y)
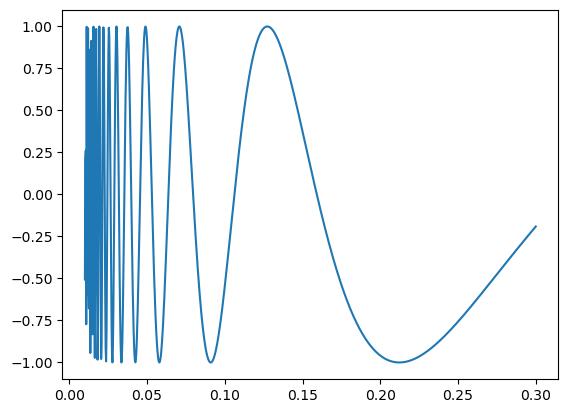
拡大図
x = np.linspace(0.01, 0.3, 1000)
y = f(x)
plt.plot(x, y)
xが0に近づくにつれ、曲線が高速振動するため、区分求積法のdxに対しすぐに周期が小さくなりすぎてしまうのです。
これに対処するためにはどうしたらよいのでしょうか。方法に移る前に、この関数の性質を確認しましょう。
# sin(1/x)の性質
一旦、この関数の性質を分析してみましょう。
x軸との交点を求めます。
$$
\sin(1/x) = 0\
\Leftrightarrow 1/x = \pi n (n = 1, 2, 3...)\
\Leftrightarrow x = \frac{1}{\pi n}\
$$
そして、関数が傾き0となる点を求めます。
$$
\frac{d\sin(1/x)}{dx} = 0 \
\Leftrightarrow -1/x^2 \cos(1/x) = 0 \
\Leftrightarrow 1/x = (1/2 + n) \pi (n = 0, 1, 2...) \
\Leftrightarrow x = \frac{1}{(1/2 + n) \pi} \
$$
関数の傾きが0となる点で、関数の値を求めます。
$$
\sin(1/\frac{1}{(1/2 + n) \pi}) = \sin((1/2 + n) \pi) = \pm 1 \
$$
以上の事実から2つのことが言えます。
- $\sin(1/x)$は$x > 1/\pi$で、$>0$を保ちながら0に漸近する。
- $\sin(1/x)$は$x <= 1/\pi$で、$\pm1$の間を振動する。
以降、$x = 1/\pi$を便宜上点Pと呼びましょう。
振動の対処
さて、元の話題に戻りますが、関数の振動に対応する方法は4つあります。それぞれを見ていきましょう。ここで、変数の説明です。
- a: 積分の始まり
- b: 積分の終わり
- n: xの範囲の分割数
- 通常の区分求積法
'''オーソドックスな方法です。ただ、高速振動部で誤差が確実に出ます。'''
a = 0.001
b = 10
n = 1000
dx = (b - a) / n
x = np.linspace(a, b, n)
y = f(x)
ans1 = sum(y * dx)
print(ans1) # 2.7355894574315376
- 半周期ごとに等分割して積分を求める
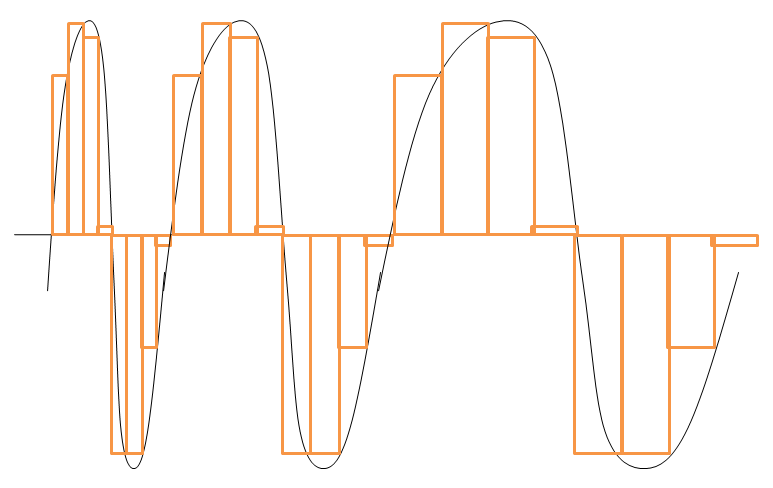
要は、sin波が高速振動してどんどん周期が狭くなっていきますが、それに応じて分割幅を狭くするということです。Pより右に関しては、単一幅の区分求積法で対応します。
イメージ図
def quadrature(x1, x2, f, n):
x = np.linspace(x1, x2, n)
y = f(x)
dx = (x2 - x1) / n
return sum(y * dx)
a = 0.001
b = 10
n = 1000
p = 1/np.pi
n2x = lambda n: 1/np.pi/n
def ans2_under_p(a, b, f, n):
an = np.floor(1/np.pi/a).astype(int)
bn = np.ceil(1/np.pi/b).astype(int)
ans2 = 0
ans2 += quadrature(a, n2x(an), f, n)
for i in range(an, bn):
ans2 += quadrature(n2x(i), n2x(i + 1), f, n)
ans2 += quadrature(n2x(bn), b, f, n)
return ans2
ans2 = 0
# p前後で計算方法を分ける
if b < p:
ans2 = ans2_under_p(a, b, f, n)
elif a > p:
ans2 = quadrature(a, b, f, n)
else:
ans2 = ans2_under_p(a, p, f, n)
ans2 += quadrature(p, b, f, n)
print(ans2) # 2.7974770570792096
- 周期の減少に伴い、区分幅を縮める
2.との違いは、区分幅を連続的に縮めるということです。
Pから左i番目のsin(1/x)の半周期分について、半周期の幅は以下となります。
$$
1/(\pi i) - 1/(\pi (i+1)) = 1/(\pi i (i + 1))
$$
つまり、$i^{-2}$に比例した区分幅でsin(1/x)を積分すればうまく積分できると考えられます。
$i = \frac{1}{\pi x}$のため、区分幅は、以下となります。
$\frac{1}{\pi i (i + 1)} = \frac{1}{\pi \frac{1}{\pi x} (\frac{1}{\pi x} + 1)} = \frac{\pi x^2}{1 - \pi x}$
a = 0.001
b = 10
n = 1000
def ans3_under_p(a, b, f, n):
ans3 = 0
x = a
while x < b:
dx = np.pi * x * x / (1 - np.pi * x) / n
ans3 += f(x) * dx
x += dx
return ans3
ans3 = 0
# p前後で計算方法を分ける
if b < p:
ans3 = ans3_under_p(a, b, f, n)
elif a > p:
ans3 = quadrature(a, b, f, n)
else:
ans3 = ans3_under_p(a, p, f, n)
ans3 += quadrature(p, b, f, n)
ans3 # 2.7223110165701425
- 変数変換
変数変換をすることでsin(1/x)の高速振動を消すことが出来ます。
$$
\int_a^b \sin(1/x) dx = \int_a^b \sin(y) d(1/y) (y = 1/x) \
\Leftrightarrow = \int_{1/a}^{1/b} \sin(y) \frac{d(1/y)}{dy} dy \
\Leftrightarrow = \int_{1/a}^{1/b} \sin(y) \frac{-1}{y^2} dy \
\Leftrightarrow = \int_{1/b}^{1/a} \sin(y) \frac{1}{y^2} dy \
$$
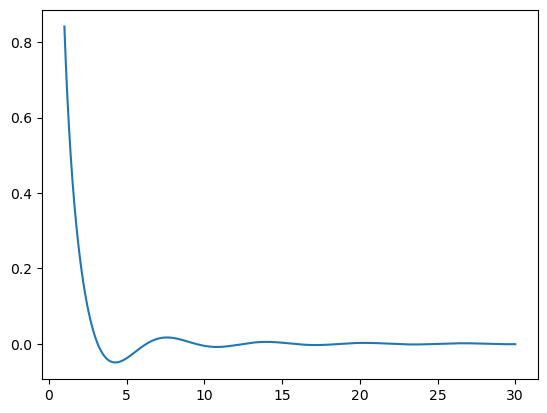
この関数は以下のような形状になります。
x = np.linspace(1, 30, 1000)
y = np.sin(x) / x / x
plt.plot(x, y)
a = 0.001
b = 10
n = 1000
f2 = lambda x: np.sin(x) / x / x
ans4 = 0
# p前後で計算方法を分ける
if b < p:
ans4 = quadrature(1 / b, 1 / a, f2, n)
elif a > p:
ans4 = quadrature(a, b, f, n)
else:
ans4 = quadrature(1 / p, 1 / a, f2, n)
ans4 += quadrature(p, b, f, n)
ans4 # 2.732169506341182
実験
これまでのコードをまとめて、精度や速度などを比較します。
コード
a = 0.001
b = 10
p = 1 / np.pi
n = 1000
f = lambda x: np.sin(1 / x)
f2 = lambda x: np.sin(x) / x / x
n2x = lambda n: 1 / np.pi / n
# ans 1
def quadrature(x1, x2, f, n):
x = np.linspace(x1, x2, n)
y = f(x)
dx = (x2 - x1) / n
return sum(y * dx)
# ans 2
def ans2_under_p(a, b, f, n):
an = np.floor(1/np.pi/a).astype(int) + 1
bn = np.ceil(1/np.pi/b).astype(int) + 1
ans2 = 0
ans2 += quadrature(a, n2x(an), f, n)
for i in range(an, bn):
ans2 += quadrature(n2x(i), n2x(i + 1), f, n)
ans2 += quadrature(n2x(bn), b, f, n)
return ans2
def equal_divide(a, b, f, n):
ans2 = 0
# p前後で計算方法を分ける
if b < p:
ans2 = ans2_under_p(a, b, f, n)
elif a > p:
ans2 = quadrature(a, b, f, n)
else:
ans2 = ans2_under_p(a, p, f, n)
ans2 += quadrature(p, b, f, n)
return ans2
# ans 3
def ans3_under_p(a, b, f, n):
ans3 = 0
x = a
while x < b:
dx = np.pi * x * x / (1 - np.pi * x) / n
ans3 += f(x) * dx
x += dx
return ans3
def decreasing_divide(a, b, f, n):
# p前後で計算方法を分ける
if b < p:
ans3 = ans3_under_p(a, b, f, n)
elif a > p:
ans3 = quadrature(a, b, f, n)
else:
ans3 = ans3_under_p(a, p, f, n)
ans3 += quadrature(p, b, f, n)
return ans3
# ans4
def variable_transformation(a, b, f, f2, n):
ans4 = 0
# p前後で計算方法を分ける
if b < p:
ans4 = quadrature(1 / b, 1 / a, f2, n)
elif a > p:
ans4 = quadrature(a, b, f, n)
else:
ans4 = quadrature(1 / p, 1 / a, f2, n)
ans4 += quadrature(p, b, f, n)
return ans4
精度
p = 1 / np.pi
n = 1000
f = lambda x: np.sin(1 / x)
f2 = lambda x: np.sin(x) / x / x
n2x = lambda n: 1 / np.pi / n
pp = p * 0.99
logspace = np.logspace(-4, np.log10(pp))
norm = [quadrature(x, pp, f, n) for x in logspace]
eqd = [equal_divide(x, pp, f, n) for x in logspace]
decdiv = [decreasing_divide(x, pp, f, n) for x in logspace]
vt = [variable_transformation(x, pp, f, f2, n) for x in logspace]
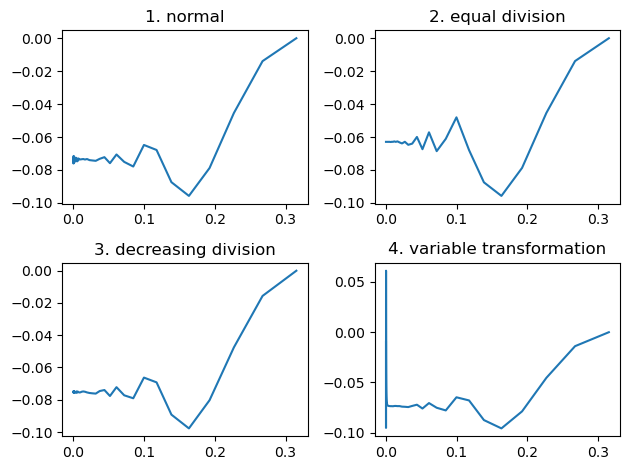
# graphs
plt.subplot(221)
plt.plot(logspace, norm)
plt.title('normal')
plt.subplot(222)
plt.plot(logspace, eqd)
plt.title('equal division')
plt.subplot(223)
plt.plot(logspace, decdiv)
plt.title('decreasing division')
plt.subplot(224)
plt.plot(logspace, vt)
plt.tight_layout()
plt.title('variable transformation')
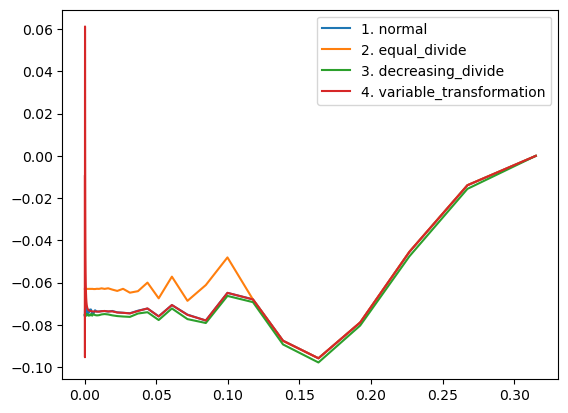
重ね合わせたグラフ
plt.plot(logspace, norm)
plt.plot(logspace, eqd)
plt.plot(logspace, decdiv)
plt.plot(logspace, vt)
plt.legend(['1. normal', '2. equal_divide', '3. decreasing_divide', '4. variable_transformation'])
速度
p = 1 / np.pi
n = 1000
f = lambda x: np.sin(1 / x)
f2 = lambda x: np.sin(x) / x / x
n2x = lambda n: 1 / np.pi / n
pp = p * 0.99
logspace = np.logspace(-4, np.log10(pp))
%timeit norm = [quadrature(x, pp, f, n) for x in logspace]
%timeit eqd = [equal_divide(x, pp, f, n) for x in logspace]
%timeit decdiv = [decreasing_divide(x, pp, f, n) for x in logspace]
%timeit vt = [variable_transformation(x, pp, f, f2, n) for x in logspace]
# 4.72 ms ± 235 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
# 10.9 ms ± 704 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
# 31.7 s ± 667 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
# 4.95 ms ± 57.4 µs per loop (mean ± std. dev. of 7 runs, 100 loops each)
結果と考察
精度
概ね、どの関数も似通った傾向となりましたが、2の当分割法のみx=0.1付近から左が乖離していました。また、4の変数変換法はx=0付近でノイズが出ました。このノイズは、積分範囲の終わりが1/aであることが原因です。aが0.001と非常に小さいとき1/a=1000となり、分割数の1000を考慮するとsin(x)の一周期がきちんと分割できていないことが原因です。これは分割数をaに反比例するように設定すれば解決すると考えられます。
速度
3.の連続的分割法が31.7秒と他に比べて1000~10000倍程度のオーダーで遅いです。微小なdxを足し上げて区分を求積し、積分範囲の終わりに達するまで続けるというアルゴリズムのためだと考えられます。他としては、2番の方法が1, 4の2倍程度の時間がかかっています。
結論
精度と速度の兼ね合いから、2か4が適切だと考えられます。