Python -連続時間マルコフ連鎖の状態遷移シミュレーション

概要

連続時間マルコフ連鎖（Continuous Time Markov Chain）の状態遷移シミュレーションを実装します．
利用するアルゴリズムはギレスピーアルゴリズム(Gillespie Algorithm)です．実装を載せたのち簡単に概略を説明しています．

離散時間マルコフ連鎖の状態遷移シミュレーションはこちらの記事を参考にするといいと思います．
Python - マルコフ連鎖状態遷移シミュレーション

実装

３状態の場合(state = 0,1,2)のマルコフ連鎖を考えます．

CTMC.py

import numpy as np
import math
import random
import matplotlib.pyplot as plt
#状態数
N=3
#遷移率行列
TRANSITION_MATRIX = [[-0.3, 0.1, 0.2],
                     [0.2, -0.9, 0.7],
                     [0.7, 0.2, -0.9]]

initial_state = 0 #初期状態
current_state = initial_state #現在の状態
next_state = 0 #次の状態
dt = 0 #状態の滞在時間

state_list = [] #状態の格納リスト
dt_list=[] #滞在時間の格納リスト
state_list.append(current_state)
dt_list.append(dt)

time = 0
T=15 #観測時間

#ギレスピーアルゴリズム(Gillespie Algorithm)
while(time <= T):
    rand_s = random.random() #状態を決定する乱数
    rand_t = random.random() #滞在時間を決定する乱数
    q =  -TRANSITION_MATRIX[current_state][current_state] #propensity function
    total = 0
#次の遷移状態を決定する
    for i in range(N):
        if(i == current_state):
            continue
        total += TRANSITION_MATRIX[current_state][i]
        if(rand_s < total/q):
            next_state  = i
            break;
    current_state = next_state
    state_list.append(current_state)
#現在の状態の滞在時間を決定する
    dt = 1/q * math.log(1/rand_t)
    time += dt
    dt_list.append(dt)
#プロット
arr_state = np.array(state_list)
arr_dt = np.array(dt_list)
arr_cumsum = np.cumsum(arr_dt)
arr_state_repeat = np.repeat(arr_state,2)
arr_time_repeat = np.repeat(arr_cumsum,2)
plt.plot(arr_time_repeat[1:],arr_state_repeat[:-1],label="state")
plt.xlabel("time")
plt.ylabel("state")
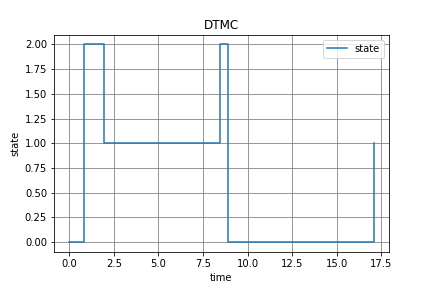
plt.title("DTMC")
plt.legend()
plt.grid(color='gray')

結果のグラフです．

状態[0,1,2]の間を時刻T=15まで遷移を繰り返しているのが見て取れます．（このグラフだと17.5付近に遷移していますが，これは仕様です．リストの最後尾を削るといった処理を行うことで取り除けますが，コードが煩雑になってしまうのでここでは取り除いていません．）

ギレスピーアルゴリズム（Giilespie Algorithm）

このアルゴリズムの主としたアイデアは,遷移率に従って
1. 次の遷移がいつ発生するか　
2. どの状態に遷移するか
の二つを，乱数によって無作為に決定するというものです．遷移率の和が大きいほどすぐに遷移しやすくなるように，また遷移率が大きい状態により遷移しやすくなるように設計されています．
詳しくは，Wikipediaをご参照ください．