推計された延滞率に対する順序性尺度によってモデルの精度を評価する。
はじめに
-
Credit scoreでは、延滞する・しないを完全に分類するよりも、どのくらいの確率で延滞するかが重要です。そして、その確率に分類された結果が正しいか正しくないかという事も重要となります。その為の代表的な指標が、完璧なモデルと予測力がないモデルと予測したモデルを順序性尺度を使って評価されたものです。
-
説明可能性についてのまとめはこちら。 理解されるPOC作成のために、機械学習したモデルをどう評価し説明するかのまとめ。
-
指標にはGini indexまたはGini coefficient(ジニ係数)、AR(Accuracy ratio) (AR値)、AUC(Area under an ROC curve)を使用します。ここで指すジニ係数=AR値で、海外ではジニ係数を日本ではAR値を使用する事が多いようです。以降はジニ係数で記載していきます。
ジニ係数
- ジニ係数とは
-
ジニ係数と言えば、「社会における所得分配の不平等さを測る指標」(wikiから引用)で一般的ですが、この理論を応用してモデルの評価に使用している物もジニ係数と呼んでいます。名前が同じなので紛らわしいです。
-
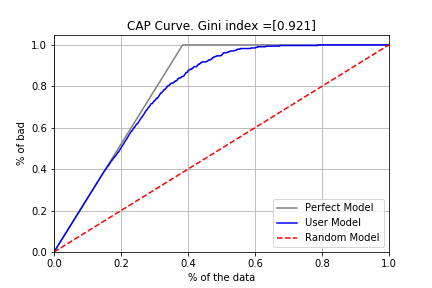
ジニ係数はCAP curve (Cumulative Accuracy Profiles) (CAP曲線)と完全予測モデル、予測力がないモデルの面積を利用して計算します。
-
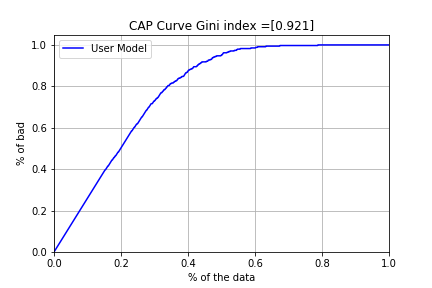
CAP曲線は予測したモデルを延滞になる確率が高い順に並べ、X軸に全債務者の累積比率を、y軸に延滞の累積比率をプロットして表した曲線です。
例えば、全債務者が20%の点で延滞全体の50%が発生している。と言うような見方になります。 -
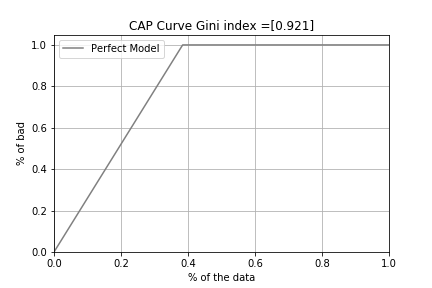
完全予測モデル(Perfect model)は、「延滞」を先に並べ、次に「延滞していない」をその後に並べてプロットしたものです。延滞したものがすべて確率が高かった順に発生した、と完全に予測できたというモデルです。
-
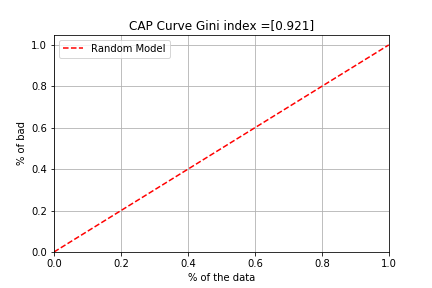
予測力がないモデル(Random model)は、45度線を描き、予測した延滞率と実際の延滞率に全く関係のないモデルです。例えば、延滞確率を高い順にならべて債務者全体の50%で延滞全体の50%が発生するようなモデルです。
- ジニ係数の計算は
-
面積をもとに算出しています。
$$
ジニ係数=\frac{CAP曲線(User Model)と予測力がないモデルライン(Random Model)の間の面積}{完全予測ライン(Perfect Model)と予測力がないモデルラインの間の面積}
$$
- プロットのコード
-
まずはサンプルのモデルを作ります。
test.py# Import Library import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.ensemble import RandomForestClassifier from sklearn.metrics import roc_auc_score from sklearn.metrics import roc_curve X_train = pd.read_csv('X_train.csv') y_train = pd.read_csv('y_train.csv') clf= RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini', max_depth=25, max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, min_samples_leaf=1, min_samples_split=15, min_weight_fraction_leaf=0.0, n_estimators=50, n_jobs=4, oob_score=False, random_state=0, verbose=0, warm_start=False) clf.fit(X_train, y_train) -
次にCAP曲線用の関数を作成します。色々探してみましたが、CAP曲線のライブラリが見つかりませんでした。サンプルコードを下記に記載しておきます。
# CAP curve from scipy import integrate def capcurve(y_values, y_proba): num_sum = np.sum(y_values) num_count = len(y_values) rate_val = float(num_sum) / float(num_count) ideal = pd.DataFrame({'x':[0,rate_val,1],'y':[0,1,1]}) xx = np.arange(num_count) / float(num_count - 1) y_cap = np.c_[y_values,y_proba] y_cap_df = pd.DataFrame(data=y_cap) y_cap_df = y_cap_df.sort_values([1], ascending=False) y_cap_df = y_cap_df.reset_index(drop=True) yy = np.cumsum(y_cap_df[0]) / float(num_sum) yy = np.append([0], yy[0:num_count-1]) percent = 0.5 row_index = np.trunc(num_count * percent) row_index = row_index.astype(np.int32) # Calculation of each area. sigma_perfect = 1 * xx[num_sum - 1 ] / 2 + (xx[num_count - 1] - xx[num_sum]) * 1 sigma_model = integrate.simps(yy,xx) sigma_random = integrate.simps(xx,xx) # Calculation of Gini index gini_value = (sigma_model - sigma_random) / (sigma_perfect - sigma_random) fig, ax = plt.subplots(nrows = 1, ncols = 1) ax.plot(ideal['x'],ideal['y'], color='grey', label='Perfect Model') ax.plot(xx,yy, color='b', label='User Model') ax.plot(xx,xx, linestyle='dashed', color='r', label='Random Model') plt.xlim(0, 1.0) plt.ylim(0, 1.05) plt.title("CAP Curve. Gini index ="+str(np.round(gini_value,4))) plt.xlabel('% of the data') plt.ylabel('% of bad') plt.grid(True) plt.legend(loc = 'lower right') plt.show() -
実行させてみます
y_pred_proba = clf.predict_proba(X=X_train) capcurve(y_values=y_train, y_proba=y_pred_proba[:,1])
AUC
- AUCとは
-
AUC (Area under curve)または(Area under an ROC curve) とはROC curve (Receiver Operatorating Characteristic curve) (ROC曲線) で描かれた内部の面積を利用して計算したものです。
-
医療業界ではc-statistic(C統計量)とも言われるそうです。
-
ROC曲線
こちらもジニ係数同様に、延滞率を高い順に並べ、各延滞確率をしきい値とした時、しきい値以上の延滞確率を延滞と予測します。それぞれのFalse Positive Rateを横軸に、True Positive Rateを縦軸にプロットしたものです。
(表はサンプルデータなのでグラフと一致していません。)-
Before
Bad Probability Bad result 8.20% 0 9.22% 0 8.41% 0 17.38% 0 15.04% 1 34.61% 1 11.50% 0 38.53% 1 9.96% 0 -
After
FPR(False Positive Rate) = FP/(FP+TN) --> X軸
TPR(True Positive Rate) = TP/(TP+FN) --> Y軸
TP(True Positive) = 正解データ正(延滞)であるものを、正しく正(延滞)と予測できた数
FP(False Positive) = 正解データ負(正常)であるものを、間違って正(延滞)と予測した数
FN(Flase Negative) = 正解データ正(延滞)であるものを、間違って負(正常)と予測した数
TN(True Negative) = 正解データ負(正常)であるものを、正しく負(正常)と予測できた数Bad Probability Bad result FPR TPR TP FP FN TN 38.53% 1 0 0.33... 1 0 2 6 34.61% 1 0 0.66... 2 0 1 6 17.38% 0 0.166... 0.66... 2 1 1 5 15.04% 1 0.166... 1.0 3 1 0 5 11.50% 0 0.2 1.0 3 1 0 4 9.96% 0 0.4 1.0 3 2 0 3 9.22% 0 0.6 1.0 3 3 0 2 8.41% 0 0.75 1.0 3 3 0 1 8.20% 0 1.0 1.0 3 3 0 0
上記の表を例にします。
まずは、延滞確率を高い順に並べます。
次に、各データが延滞だった場合には、まずY軸が動きます。
上記の表の場合は、FPRが0(X軸が0)の場合は、TPRの値(Y軸が0.33..,0.66..)だけが変化しています。
CAP曲線の場合はX軸とY軸が同時に動きますが、ここでは、X軸が同じ数字になる事も考えられるため、CAP曲線の動きとは違い、Y軸のみが変化するという事がありえます。それが、CAP曲線とROC曲線との違いになります。
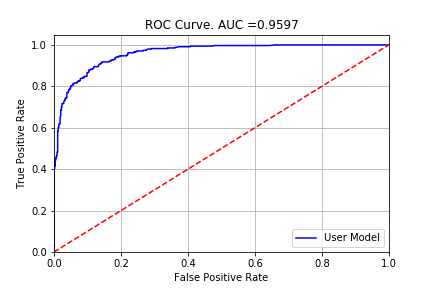
-
- プロットのコード
-
AUC値、ROC曲線ともにsklearnで準備されているので、そちらを使用します。
AUC値はroc_auc_score()、ROC曲線はroc_curve()です。# AUC roc_auc_value=roc_auc_score(y_train, clf.predict_proba(X_train)[:,1]) # ROC curve fpr_rf,tpr_rf,thresholds_rf=roc_curve(y_train, clf.predict_proba(X_train)[:,1]) plt.plot(fpr_rf,tpr_rf,'b', label='User Model') plt.plot([0, 1], [0, 1], 'r--') plt.xlim([0.0, 1.0]) plt.ylim([0.0, 1.05]) plt.xlabel('False Positive Rate') plt.ylabel('True Positive Rate') plt.title("ROC Curve. AUC ="+str(np.round(roc_auc_value,4))) plt.grid(True) plt.legend(loc = 'lower right') plt.show()
まとめ
まとめ
- ジニ係数・AUCとも完全予測モデルにどれだけ近いかを数値化しています。ジニ係数はランダムモデルを規準に、完全予測モデルの面積からランダムモデルの面積を引き、残りが何%の面積を占めているかを表しています。
AUCは完全予測モデルの面積の何%を占めているかを表しています。 - ジニ係数・AUC=1の時が完全予測モデルと一致となる。1に近いほどいいモデルと言えます。
ただし、個人向けCredit scoreでは、このような0.9を超える場合、過学習の可能性が非常に高いです。
一般的にはジニ係数で0.3-0.7あたりで、債務者がサブプライム層だったり、銀行系顧客などで違ってきます。 - CAP曲線の方が全体の債務者に対しての延滞発生傾向がわかりやすくなります。
- ジニ係数とAUCは曲線の書き方の違いだけになるため、ジニ係数とAUCは正比例の関係になります。
ジニ係数 = 2AUC -1
上記のCAP曲線内のコードでジニ係数を計算するより、AUCから計算した方が簡単になります。CAP曲線を描く必要がある時は関数化し、一緒にジニ係数を計算します。 - 指標数値とグラフを見るだけで相手に理解してもらえる訳ではないので、グラフのX軸、Y軸は何なのかを説明できるとよりイメージしやすくなります。
- ジニ係数とAUCは、確率の順位性の正確性を表しています。ただし、確率の数値の正確性は表すことができないので、他の指標を用いる必要があります。
関連・参考記事
-
金融リスクと統計的学習
CAP曲線とROC曲線の違いもわかりやすく説明されています。