前書き
ThethingsNetworkにつながるゲートウェイやエンドデバイスをラズパイで作っています.
Uplinkは少しはできるようになったのですがDownlinkがなかなかできません..
気分転換?に前から気になっていたLoRa変調について調べてみたのでメモとして記します.
もし間違いなど見つけられたら指摘していただけるとうれしいです.
LoRa変調
技術的にはChirp Spread Spectrum、チャープ・スペクトラム拡散による変調のことですが
Long Rangeを略してLoRa、その用途に適した変調ということでLoRa変調と呼ばれています.
広範囲の通信に適した変調ということでしょうか.
図による説明
チャープは周波数を時間とともに変化させて拡散する方法でFig.1のように変化させます.
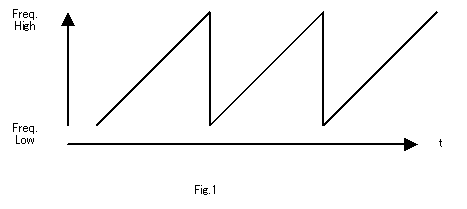
周波数はFreq.LowからFreq.Highの範囲で変化させます.Freq.High-Freq.Lowが帯域幅BWになります.
$BW = Freq.High - Freq.Low$
図は時間とともに周波数が増加していますが減少する方向に変化させてもよいです.
そして周波数が一周して元に戻る?までの時間が1シンボル(変調の単位)となります.Fig.1では3シンボルあります.
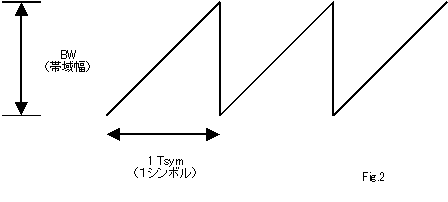
シンボルは通信の変調の単位ですがデータの1/0をどうやって対応させるかや何通りの波形があって何ビットに対応させるかは決め方次第です.
LoRa変調ではデータをシンボルの開始周波数(Freq.LowとGreq.Highの間の位置)に割り当てています.
ここでは1シンボルに8ビットを割り当てるとして変調した例をFig.3に示します.
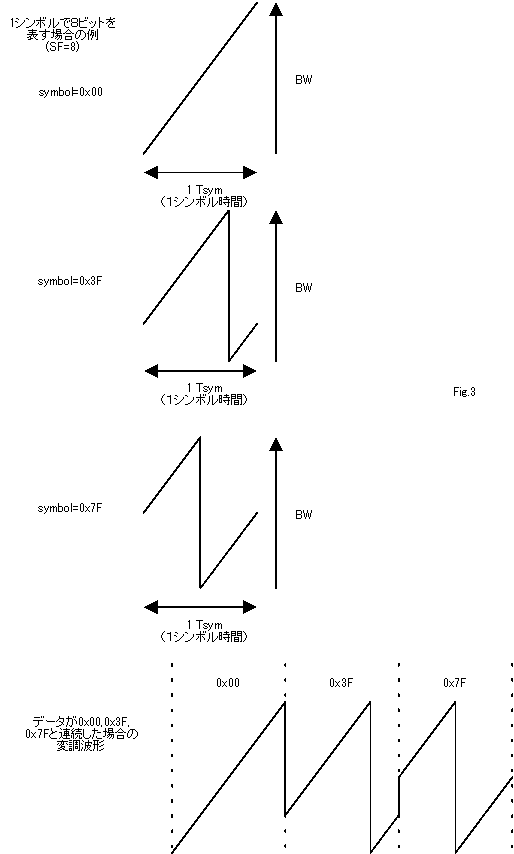
データが0x00、0x3F、0x7Fと続いた場合の変調波形がこの図です.
図では2ビット分しか書いていませんがBWを256($=2^8$)分割すれば8ビット分のデータを割り当てることができます.
ここで1シンボルに割り当てたビット数を$SF$とします.(後述)
式による説明
Chirp変調では拡散は周波数の変化で、その大きさは$BW$ですのでチップレート($R_c$)は$BW$と言えます.
シンボルレート($R_{sym}$)はチップレートをシンボル数 $2^{SF}$で割ればよく次の式になります.
$R_{sym}=\dfrac{BW}{2^{SF}}$
ビットレート$R_{bit}$は先の$SF$を用いて
$R_{bit}=\dfrac{BW}{2^{SF}}SF$
となります. また、1シンボル時間$T_{sym}$は$R_{sym}$から
$T_{sym}=\dfrac{2^{SF}}{BW}$
となります.
周波数が$f_h$から$f_l$へジャンプするタイミングは$\dfrac{1}{BW}$ごとでFig.4のようになります.
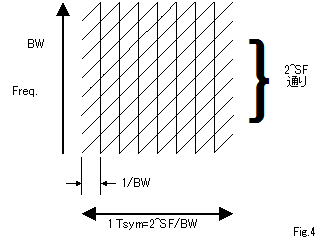
LoRa変調について技術的に踏み込んで説明してあるものがなかなかなくて前から知りたいと思っていましたのですっきりしました.
参考にしたサイト
https://www.sghoslya.com/p/lora_9.html
https://www.youtube.com/c/mobilefish/about