目的
2/1からの最高気温を累積していくと600度に達したときにさくらが開花するという600度の法則がある。この法則について、過去の気温データを使ってどれくらい確からしいのか検証する。
600度の法則とは、「2月1日以降の日最高気温の合計が600℃に達すると開花とする」という法則。ウェザーニュースのサイトより。
600度の法則の起点となる、1年で最も寒い時期の2月1日に合わせてこの記事を投稿しました。
データ(さくら開花日)のダウンロードと読み込み
さくらの開花日(2021-2023年)から、開花日データをダウンロードする。このページから過去にさかのぼって1953年までのデータがダウンロードできる。
最新のファイル(2021年からのデータ)を見ると、以下のようになっている。
地点名,2021,2022,2023,平年値,代替種目,,,,,
,月,日,月,日,月,日,月,日,,
,,,,,,,,,,
稚内,*,5,8,5,6,5,3,5,13,えぞやまざくら
留萌,-,-,-,-,えぞやまざくら,,,,,
旭川,*,4,29,4,26,4,25,5,4,えぞやまざくら
;(後略)
2021年から2023年までの、3年分しかないが、通常は2011年から2020年まで、など、10年分のデータが記載される。また、始まりが1953年からなので、そのファイルも1953年から1960年までの8年分しかない。扱いが難しいので、開始年と年数をリスト化する。
# 開花宣言日のファイル一覧
open_day_file_list = [
#開始年、年数
[1953,8],
[1961,10],
[1971,10],
[1981,10],
[1991,10],
[2001,10],
[2011,10],
[2021,3],
]
そめいよしので宣言している都市のみをピックアップする。北の北海道は、えぞやまざくらが多いが、札幌、室蘭、函館はそめいよしのである。南の沖縄は、ひがんざくらが多く、那覇も対象外となるので、最南端の都市は鹿児島となる。
47都道府県+2(北海道札幌以外)-1(沖縄)=48都市分のデータとなる。
以下、北から順に地方別にリスト化する。
# 2023年まで、気象庁がそめいよしので開花宣言していた都市のみをピックアップする
city_list = [
'札幌','室蘭','函館',
'青森','盛岡','仙台','秋田','山形','福島',
'水戸','宇都宮','前橋','熊谷','銚子','東京','横浜',
'新潟','富山','金沢','福井','甲府','長野','岐阜','静岡','名古屋','津',
'彦根','京都','大阪','神戸','奈良','和歌山',
'鳥取','松江','岡山','広島','下関',
'徳島','高松','松山','高知',
'福岡','佐賀','長崎','熊本','大分','宮崎','鹿児島',
]
基本的には見るためのデータなので、プログラムで読むのが面倒であるが、以下の関数で整形化する。
- 縦が都市、横が年毎の開花日を月、日のカンマ区切り。
- 年、月、日を文字列連結して、日付型に変換する。
- 横方向に1年分ずつ処理し、横が都市、縦が年になるように、転置して結合する。
- 観測しなくなった都市もあるので、その場合は空欄(ハイフン)
- ハイフンを除外する。
import pandas as pd
# 開花宣言日のファイルを読み込んで、整形した上で、Dataframeを返す関数
def read_open_day_file(start_year,num_year):
# 開花宣言日のファイルの読み込み
filename = './Data/' + str(start_year) + '.csv'
df_input = pd.read_csv(filename,index_col=0)
# 分析対象の都市に絞る
df_input = df_input.loc[city_list]
# 整形したDataframe(返却用)
df_openday = pd.DataFrame()
# 年のループ
for i, year in enumerate(range(start_year,start_year+num_year)):
month_index = 1 + 2*i
day_index = 1 + 2*i + 1
# 開花宣言日をdate型に変換するためのDataframe(1年分)
df_one_year = pd.DataFrame()
# 年月日をそれぞれ取得
df_one_year['month'] = df_input.iloc[:,month_index]
df_one_year['day'] = df_input.iloc[:,day_index]
df_one_year['year'] = year
# データなし(-)を除外
df_one_year = df_one_year[df_one_year['month']!='-']
# 文字列に変換
df_one_year['year'] = df_one_year['year'].astype('str')
df_one_year['month'] = df_one_year['month'].astype('str')
df_one_year['day'] = df_one_year['day'].astype('str')
# 年月日を統合
df_one_year['date'] = df_one_year['year'] + '/' + df_one_year['month'] + '/' + df_one_year['day']
# date型に変換
df_one_year['date'] = pd.to_datetime(df_one_year['date'])
# 不要列を削除
df_one_year = df_one_year.drop(['month','day','year'],axis=1)
# これまでのデータと統合
df_openday = pd.concat([df_openday,df_one_year.T],axis=0)
return df_openday
# 最新のファイルを読み込む(試し読み)
read_open_day_file(2021,3)
地点名 札幌 室蘭 函館 青森 盛岡 仙台 秋田 山形 福島 水戸 ... 高松 松山 高知 福岡 佐賀 長崎 熊本 大分 宮崎 鹿児島
date 2021-04-22 2021-04-27 2021-04-20 2021-04-13 2021-04-09 2021-03-28 2021-04-04 2021-04-02 2021-03-25 2021-03-20 ... 2021-03-15 2021-03-15 2021-03-15 2021-03-12 2021-03-17 2021-03-14 2021-03-17 2021-03-18 2021-03-16 2021-03-17
date 2022-04-23 2022-04-25 2022-04-21 2022-04-16 2022-04-14 2022-04-08 2022-04-12 2022-04-11 2022-04-04 2022-03-30 ... 2022-03-24 2022-03-21 2022-03-19 2022-03-17 2022-03-19 2022-03-22 2022-03-20 2022-03-23 2022-03-18 2022-03-20
date 2023-04-15 2023-04-21 2023-04-14 2023-04-07 2023-04-03 2023-03-26 2023-04-04 2023-03-31 2023-03-24 2023-03-20 ... 2023-03-22 2023-03-18 2023-03-17 2023-03-18 2023-03-22 2023-03-21 2023-03-22 2023-03-24 2023-03-19 2023-03-24
3 rows × 48 columns
全期間のデータを読み込む。1ファイルずつ読み込んで、concatで結合していく。
# 開花宣言日のファイルの読み込み
df_openday = pd.DataFrame()
# 開花宣言日のファイル一覧のループ
for open_day_file in open_day_file_list:
start_year = open_day_file[0]
num_year = open_day_file[1]
# 開花宣言日のファイルを読み込んで、整形した上で、Dataframeを返す関数
df_temp = read_open_day_file(start_year,num_year)
# これまでのデータと統合
df_openday = pd.concat([df_openday,df_temp],axis=0)
df_openday.head()
地点名 札幌 室蘭 函館 盛岡 仙台 秋田 山形 福島 水戸 宇都宮 ... 福岡 佐賀 長崎 熊本 大分 鹿児島 奈良 高知 青森 宮崎
date 1953-05-07 1953-05-10 1953-05-02 1953-04-27 1953-04-11 1953-04-22 1953-04-19 1953-04-09 1953-04-04 1953-04-06 ... 1953-03-28 1953-03-26 1953-03-26 1953-03-28 1953-03-26 1953-03-29 NaT NaT NaT NaT
date 1954-05-04 1954-05-07 1954-05-03 1954-04-19 1954-04-06 1954-04-17 1954-04-13 1954-04-05 1954-04-01 1954-04-02 ... 1954-03-28 1954-03-27 1954-03-27 1954-03-26 1954-03-27 1954-03-31 1954-03-27 1954-03-25 NaT NaT
date 1955-05-11 1955-05-18 1955-05-08 1955-04-18 1955-04-11 1955-04-16 1955-04-12 1955-04-09 1955-03-29 1955-04-03 ... 1955-03-24 1955-03-24 1955-03-24 1955-03-21 1955-03-25 1955-03-29 1955-03-27 1955-03-21 NaT NaT
date 1956-05-04 1956-05-08 1956-05-03 1956-04-24 1956-04-16 1956-04-21 1956-04-18 1956-04-14 1956-04-09 1956-04-10 ... 1956-04-02 1956-03-29 1956-03-28 1956-03-25 1956-03-31 1956-03-27 1956-04-02 1956-03-24 1956-04-26 NaT
date 1957-05-09 1957-05-08 1957-05-08 1957-04-27 1957-04-16 1957-04-24 1957-04-20 1957-04-15 1957-04-08 1957-04-09 ... 1957-04-01 1957-03-31 1957-03-30 1957-03-29 1957-04-06 1957-04-01 1957-04-07 1957-04-02 1957-05-01 NaT
5 rows × 48 columns
データ(日毎の最高気温)のダウンロードと読み込み
気象庁のサイトから、各都市の気温データをダウンロードする。
- 選択地点:札幌、室蘭など、48都市分を個別にダウンロードする。(データ容量制限で1都市ずつしかダウンロードできない)
- 選択項目:日最高気温
- 選択期間:2月1日から5月31日までの日別値を1953年から2023年まで表示
48都市分のデータをダウンロードし、Dataフォルダ以下に、都市名.csv というファイル名で保存し、以下のように読み込んで、2月1日から開花日までの最高気温を累積計算していく。
import datetime
output_city_list = []
output_year_list = []
output_temp_list = []
# 都市のループ
for city in city_list:
# 気温データ読み込み
filename = './Data/' + city + '.csv'
df_tempreture = pd.read_csv(filename,encoding='shift-jis',header=None)
df_tempreture = df_tempreture.rename(columns={0: 'date',1: 'tempreture'})
df_tempreture['date'] = pd.to_datetime(df_tempreture['date'])
df_tempreture = df_tempreture.drop(df_tempreture.columns[[2, 3]], axis=1)
# 対象の都市の開花日を抽出
df_openday_city = df_openday[city]
# 無効データを削除
df_openday_city = df_openday_city.dropna()
# 年のループ
for i, openday in df_openday_city.iteritems():
# 最高気温累積の開始日
startday = datetime.datetime(openday.year, 2, 1, 0, 0, 0 )
# 開花日
openday = datetime.datetime(openday.year, openday.month, openday.day, 23, 59, 59 )
# 最高気温累積の開始日から開花日までを抽出
df_tempreture2toOpen = df_tempreture[(startday<=df_tempreture['date']) & (df_tempreture['date']<=openday)]
# 最高気温の累積を計算
accumulated_tempreture = df_tempreture2toOpen['tempreture'].sum()
output_city_list.append(city)
output_year_list.append(openday.year)
output_temp_list.append(accumulated_tempreture)
df_output = pd.DataFrame([output_city_list,output_year_list,output_temp_list])
df_output = df_output.T
df_output = df_output.rename(columns={0: '都市',1: '年',2:'最高気温累積'})
df_output['最高気温累積'] = df_output['最高気温累積'].astype('float')
print(df_output.head())
print(df_output.tail())
都市 年 最高気温累積
0 札幌 1953 520.2
1 札幌 1954 557.9
2 札幌 1955 587.8
3 札幌 1956 561.7
4 札幌 1957 564.4
都市 年 最高気温累積
3379 鹿児島 2019 878.9
3380 鹿児島 2020 1061.1
3381 鹿児島 2021 818.8
3382 鹿児島 2022 748.9
3383 鹿児島 2023 925.9
北の札幌から、南の鹿児島までの、各年の最高気温累積が取得できた。
開花までの最高気温累積をヒストグラムで可視化
累積気温をヒストグラムで可視化する。
import matplotlib.pyplot as plt
import japanize_matplotlib
plt.hist(df_output['最高気温累積'])
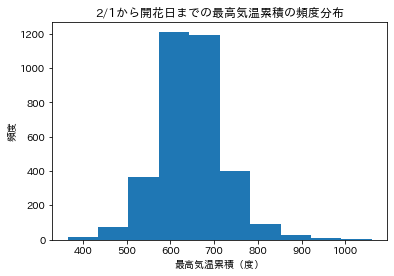
plt.title('2/1から開花日までの最高気温累積の頻度分布')
plt.xlabel('最高気温累積(度)')
plt.ylabel('頻度')
plt.show()
tempreture_mean = df_output['最高気温累積'].mean()
tempreture_std = df_output['最高気温累積'].std()
print(f'平均:{tempreture_mean:.1f}度')
print(f'標準偏差:{tempreture_std:.1f}度')
平均:647.3度
標準偏差:74.3度
600度、700度が多いので、600度の法則はあっていそうだが、平均が647.3度とちょっと高めのようである。
また、400度や1000度の場合もあり、標準偏差も74.3度とばらついている。
年代別の変化
年代で変わってきているのかを確認してみるが、
# 年毎に箱ひげ図を表示
df_output_year = []
year_list = range(1953,2024)
# 年のループ
for year in year_list:
df_output_one_year = df_output[df_output['年']==year]
df_output_year.append(df_output_one_year['最高気温累積'])
plt.figure(figsize=[15,4])
plt.boxplot(df_output_year,labels=year_list)
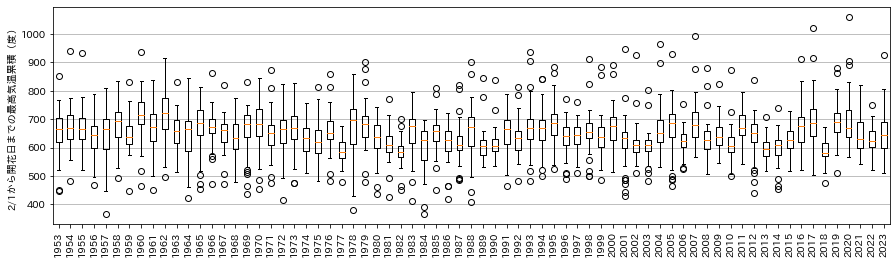
plt.ylabel('2/1から開花日までの最高気温累積(度)')
plt.xticks(rotation=90)
plt.grid(axis='y')
plt.show()
温暖化の影響などは考えにくい。
都市による違い
最高気温累積が低いケースと高いケースを見てみると、
print(df_output.sort_values('最高気温累積').head())
print(df_output.sort_values('最高気温累積').tail())
都市 年 最高気温累積
101 室蘭 1984 364.4
74 室蘭 1957 367.4
95 室蘭 1978 379.9
30 札幌 1984 392.2
105 室蘭 1988 409.6
都市 年 最高気温累積
3361 鹿児島 2001 946.4
3364 鹿児島 2004 963.9
3367 鹿児島 2007 992.7
3377 鹿児島 2017 1020.0
3380 鹿児島 2020 1061.1
低いのは室蘭(札幌)で、300度台でも開花する。
一方、高いのは鹿児島で、1000度台でようやく開花する。
都市毎に箱ひげ図をプロットすると、
# 都市毎に箱ひげ図を表示
df_output_city = []
# 都市のループ
for city in city_list:
df_output_one_city = df_output[df_output['都市']==city]
df_output_city.append(df_output_one_city['最高気温累積'])
plt.figure(figsize=[15,4])
plt.boxplot(df_output_city,labels=city_list)
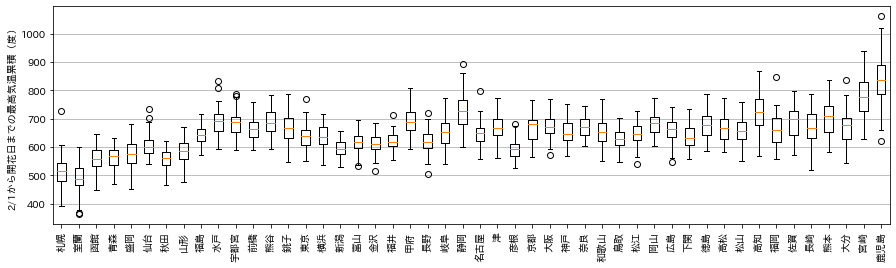
plt.ylabel('2/1から開花日までの最高気温累積(度)')
plt.xticks(rotation=90)
plt.grid(axis='y')
plt.show()
北海道・東北などの北日本は低く、鹿児島・宮崎・高知・静岡などの太平洋側南部は高い傾向がある。
冬(2月)の平均気温の影響
北部と南部の違いとして、2月の平均気温がありそうなので、2月の平均気温と最高気温累積を散布図にプロットする。
もう一度気温データを読み込み、2月の平均気温を取得する。
なお、1月の気温も使いたいのだが、データダウンロードからやり直す必要があるので、2月の平均気温とする。
2月の平均気温の取得
import datetime
output_temp2_list = [] # 2月の気温平均
# 都市のループ
for city in city_list:
# 気温データ読み込み
filename = './Data/' + city + '.csv'
df_tempreture = pd.read_csv(filename,encoding='shift-jis',header=None)
df_tempreture = df_tempreture.rename(columns={0: 'date',1: 'tempreture'})
df_tempreture['date'] = pd.to_datetime(df_tempreture['date'])
df_tempreture = df_tempreture.drop(df_tempreture.columns[[2, 3]], axis=1)
# 対象の都市の開花日を抽出
df_openday_city = df_openday[city]
# 無効データを削除
df_openday_city = df_openday_city.dropna()
# 年のループ
for i, openday in df_openday_city.iteritems():
# 2月の平均気温
february_first_day = datetime.datetime(openday.year, 2, 1, 0, 0, 0 )
march_first_day = datetime.datetime(openday.year, 3, 1, 0, 0, 0 )
df_tempreture3 = df_tempreture[(february_first_day<=df_tempreture['date']) & (df_tempreture['date']<march_first_day)]
feb_mid_mean_tempreture = df_tempreture3['tempreture'].mean()
output_temp2_list.append(feb_mid_mean_tempreture)
df_output['2月の平均気温'] = output_temp2_list
df_output.head()
都市 年 最高気温累積 2月の平均気温
0 札幌 1953 520.2 -1.507143
1 札幌 1954 557.9 1.032143
2 札幌 1955 587.8 0.167857
3 札幌 1956 561.7 0.296552
4 札幌 1957 564.4 -0.660714
2月の平均気温と累積気温の散布図
# 2月上旬の気温平均と2/1から開花日までの最高気温累積(度)を散布図で可視化
plt.scatter(df_output["2月の平均気温"], df_output["最高気温累積"])
plt.xlabel("2月の平均気温")
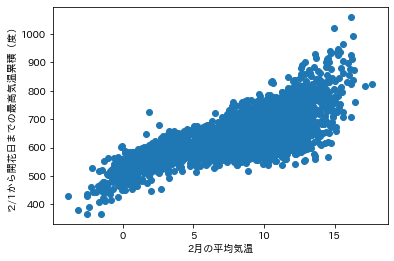
plt.ylabel("'2/1から開花日までの最高気温累積(度)")
plt.show()
# 相関係数
print('相関係数')
print(df_output.corr())
相関係数
最高気温累積 2月の平均気温
最高気温累積 1.000000 0.722131
2月の平均気温 0.722131 1.000000
散布図から、正の相関があることがわかる。
相関係数も、0.72となり、強い相関である。
回帰分析
説明変数を2月の平均気温、目的変数を最高気温累積として回帰分析をする。
回帰係数を出力し、回帰直線を可視化する。
from sklearn.linear_model import LinearRegression
import numpy as np
# 回帰分析
x = df_output[['2月の平均気温']]
y = df_output["最高気温累積"]
model_lr = LinearRegression()
model_lr.fit(x,y)
# 回帰係数
a = float(model_lr.coef_)
b = model_lr.intercept_
print(f'回帰係数=',a)
print('切片=',b)
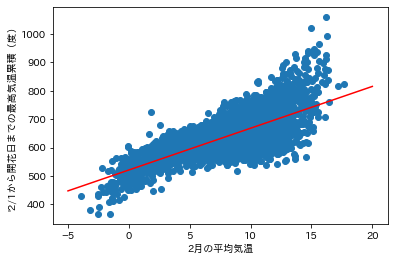
# 2月上旬の気温平均と2/1から開花日までの最高気温累積(度)を散布図で可視化
plt.scatter(df_output["2月の平均気温"], df_output["最高気温累積"])
plt.xlabel("2月の平均気温")
plt.ylabel("'2/1から開花日までの最高気温累積(度)")
x = np.array([-5, 20])
y = a * x + b
plt.plot(x,y, color='red')
plt.show()
回帰係数= 14.727711814813489
切片= 521.1632074717072
切片が521なので、2月の平均気温が0度の場合、累積気温521度で開花する。回帰係数が14なので、平均気温が1度高く(低く)なると、14度高い(低い)累積気温で開花する。日本は縦に長く、2月の平均気温でも約20度の幅があり、それにより、開花までの累積気温も変化する。(600度のばらつきの一因が、2月の平均気温の差と考えられる。)
なので、地域によっては、600度の法則にはならないこともあるが、このような法則は、首都東京であてはまりがよいと推測する。東京のデータを見てみると、
df_tokyo = df_output[df_output['都市']=='東京']
print(df_tokyo['最高気温累積'].mean())
print(df_tokyo['2月の平均気温'].mean())
638.1253521126761
10.447783251231527
やはり、2月の平均気温が10度となる東京が、600度で開花するという法則に、あてはまりがよさそうである。
まとめ
- 600度の法則について、48都市、70年分の過去の気温データで検証したところ、平均647.3度、標準偏差74.3度と、少し高めでばらついているが、まずまず当たっている結果が得られた。
- 600度より低い温度で開花するのは北の寒い地域、600度より高い累積気温で開花するのは南の暖かい地域であることがわかった。
- 2月の平均気温との相関係数は、0.72と強い相関がある。
- 2月の平均気温が0度の場合、累積気温521度で開花し、1度高く(低く)なると14度高い(低い)累積気温で開花する。
- 東京の2月の平均気温が10度となるので、600度の法則というのだろう。
- もし、東京がもう少し、寒い/暖かい地域にあったら、500度の法則や700度の法則となっていた可能性がある。
おまけ(さくらの魅力)
さくらは寒い時期から、開花の準備を始め、3月4月にようやく暖かくなりだしたころに一斉に咲きだす。暖かくなってから準備をするのではなく、寒い時期から準備している、というのは、教訓めいている。寒い時期(逆境の時期)でも、将来(暖かくなること)を予測して準備をしている、ということは、何かを成し遂げるには、例え逆境にあっても、将来を見据えて、コツコツと準備をしていくことが必要だ、と言っているようである。
さらに、冬が寒いほうが、累積温度が低くとも、早く開花するということは、北の寒い冬を過ごしたさくらを、春先に南の暖かい地域に持って行くと、(現実的には難しいだろうが、)南で暖かい冬を過ごしたさくらより、早く開花する、ということだ。厳しい逆境に耐え抜くことにより、何かを成し遂げるための条件(ハードル)が低くなる=成功の可能性が高くなる、という解釈をするのは、拡大解釈しすぎであろうか?下積みの長い俳優さんや芸人さんが苦労を重ねた結果、超売れっ子になったり、空気の薄い高地でトレーニングした長距離ランナーが好成績を残したり、と重なって見える。
さくらは、美しく咲く、そして、潔く散る、だけでなく、このような生き方も示唆してくれる魅力的な樹木であり、今回の分析により、さくらの魅力がまた一つ増えた。