背景
統計検定2級の受験を目指し、CBT公式問題集を解いて、だいたい解答できそうなレベルにまで達したが、回答時間がかかっている。特に、電卓を使った計算が必要な問題や、確率の面倒くさい問題など、何度やっても時間がかかっていたので、きちんと計測しておいたほうが良いと思った。
目的
過去に3回くらいは解いていると思うので、4回目を解くときに、解答時間を計測し、1回だけではつまらないので、5回目も解いてみて、解答時間が早くなっているかを検証したい。
試験全体では、通常35問出題されるので、その35問を解くのにどれくらい時間がかかるかを予測したい。(何回も解いた問題であるが、ペース配分を見積もりたい。)
解答時間の計測と読み込み
何回も解いていると、問題を見ただけでわかってしまう問題もあるが、問題文をきちんと読んで、すんなり解答できた想定でもこれくらいはかかるであろう時間を計測した。
解答時間を計測し、"解答時間.xlsx"に記録し、それを読み込むと以下の通りとなる。
import pandas as pd
# 解答時間をまとめたエクセルを読み込み
df_time = pd.read_excel('解答時間.xlsx', index_col=[0,1])
print(df_time.head())
4th 5th
Category No
1 1 48 33
2 84 34
3 51 55
4 57 60
5 19 25
カテゴリ毎に分析するので、カテゴリリストを取得する。
# カテゴリのリストを取得
category_list = df_time.index.get_level_values(0)
category_list = set(category_list)
category_list = list(category_list)
category_list.sort()
category_list
[1, 2, 3, 4, 5, 6, 7, 8, 91, 92, 101, 102]
9章と10章は、2部構成なので、91,92,101,102とした。
ちなみに、各カテゴリの内容は以下の通りである。
| Category | 内容 |
|---|---|
| 1 | 1変数記述統計の分野 |
| 2 | 2変数記述統計の分野 |
| 3 | データ収集の分野 |
| 4 | 確率の分野 |
| 5 | 確率分布の分野 |
| 6 | 標本分布の分野 |
| 7 | 推定の分野 |
| 8 | 検定の分野 |
| 9 | カイ二乗検定の分野 |
| 9-1 | 適合度検定の分野 |
| 9-2 | 独立性検定の分野 |
| 10 | 線形モデルの分野 |
| 10-1 | 回帰分析の分野 |
| 10-2 | 分散分析の分野 |
# 以降、カテゴリ内での問題番号は不要なので削除
df_time = df_time.reset_index()
df_time = df_time.drop('No',axis=1)
print(df_time.head())
Category 4th 5th
0 1 48 33
1 1 84 34
2 1 51 55
3 1 57 60
4 1 19 25
グラフ化しやすいように、縦に並べる。
# 4回目と5回目を分離し、縦に並べる
def get_Nth(df,Nth):
df_Nth = df_time[['Category',Nth]].copy()
df_Nth = df_Nth.rename(columns={Nth:'time'})
df_Nth['Nth'] = Nth
return df_Nth
df_4th = get_Nth(df_time,'4th')
df_5th = get_Nth(df_time,'5th')
df_45th = pd.concat( [df_4th,df_5th] )
print(df_45th.head())
print(df_45th.tail())
Category time Nth
0 1 48 4th
1 1 84 4th
2 1 51 4th
3 1 57 4th
4 1 19 4th
Category time Nth
81 102 165 5th
82 102 135 5th
83 102 18 5th
84 102 198 5th
85 102 86 5th
解答時間の可視化
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns
# 箱ひげ図の描画
sns.boxplot(x="Category", y="time", data=df_45th,hue="Nth")
plt.show()

この箱ひげ図を見ただけでも、5回目が、4回目より早くなったとは思えないが、、、
4回目より5回目のほうが早く解答できたかの検定
以下の仮説を立て、検定してみる。
帰無仮説:4回目と5回目の解答時間は同じである
対立仮説:4回目より、5回目の解答時間は早くなった
from scipy import stats
import numpy as np
def t_test(df1,df2,Category):
data1 = df1[df1['Category']==Category]['time']
data2 = df2[df2['Category']==Category]['time']
t_statistic, p_value = stats.ttest_ind(data1, data2, equal_var=False,alternative='less')
t_p_value = f"t:{t_statistic:.2f} p:{p_value:.4f}"
return p_value
np_p_value_list = np.empty(0)
text_category_list = list()
for category in category_list:
p_value = t_test(df_4th,df_5th,category)
np_p_value_list = np.append(np_p_value_list,p_value)
text_category_list.append(str(category))
plt.plot(text_category_list,np_p_value_list)
plt.title('P-value')
plt.xlabel('category')
plt.ylim(0,1)
plt.show()

P値が大きいので、帰無仮説は棄却できない。
やはり、電卓を使ったり、面倒くさい計算をしたりするので、何回解いても、解答時間は変わらない、ということがわかった。
35問を解く時間の予測
35問出題されるとして、ランダムに解答時間を35問分抽出し、90分の試験時間で終わるかをブートストラップ法で検証してみた。
n_bootstrop = 1000
n = 35
np_time_list = np.empty(0)
for i in range(1000):
sample = df_45th['time'].sample(n=n).values
# 秒を分に変換してリストに格納
np_time_list = np.append(np_time_list, sample.sum()/60)
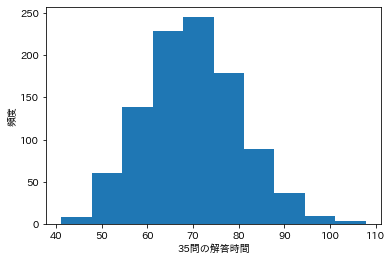
plt.hist(np_time_list)
plt.xlabel('35問の解答時間')
plt.ylabel('頻度')
plt.show()
何回も解いた問題でも、35問となると、平均でも70分、場合によっては試験時間の90分以上かかることもあることがわかった。
まとめ
実際のテストとなると、新規の問題となるので、時間が足りないことが予想される。時間かかりそうな問題は容赦なくスキップし、解ける問題から確実に解いていくのがよいと思った。