各種確率分布のまとめ

統計検定準１級受験対策用に各種確立分布を一覧でまとめました。

参考としたのは下記の統計学実践ワークブックです。

※筆者が所属するNPO法人の勉強用にメモしたものです。専門領域でないため誤りや誤解があるかと思いますので、加筆修正すべきことろがありましたらご指摘ください。継続してブラッシュアップしていきます。

©2022 NPO法人AI開発推進協会

確率分布一覧表

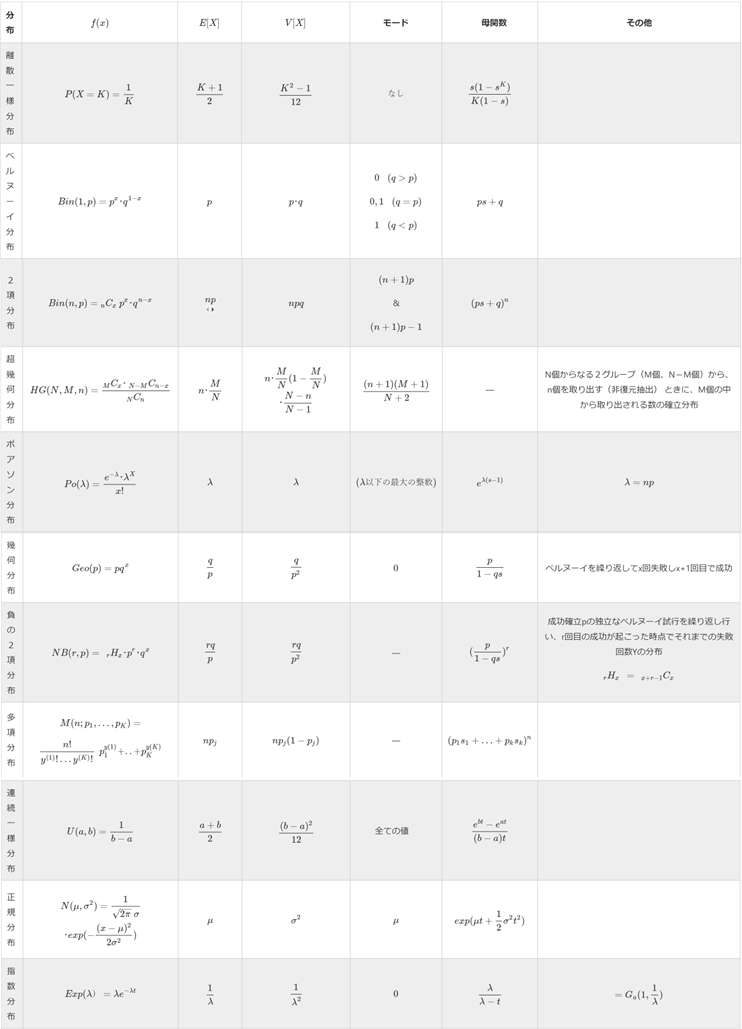
分布	$$f(x)$$	$$E[X]$$	$$V[X]$$	モード	母関数	その他
離散一様分布	$$P(X=K)=\frac{1}{K}$$	$$\frac{K + 1}{2}$$	$$\frac{K^2 -1}{12}$$	$$ なし $$	$$\frac{s(1 - s^K)}{K(1 - s)}$$
ベルヌーイ分布	$$Bin(1, p)=p^x･q^{1 - x}$$	$$p$$	$$p･q$$	$$ 0\hspace{4mm} (q > p)$$ $$0, 1 \hspace{4mm}(q = p)$$ $$ 1 \hspace{4mm}(q < p) $$	$$ps + q$$
２項分布	$$Bin(n, p)={}_{n}C_x\hspace{1mm}p^x･q^{n-x}$$	$$np$$	$$npq$$	$$(n + 1)p$$ & $$(n + 1)p - 1$$	$$(ps + q)^n$$
超幾何分布	$$HG(N, M, n)=\frac{_MC _x ･ \hspace{1mm} _{N-M}C _{n-x}}{{}_NC_n} $$	$$n･\frac{M}{N}$$	$$n･\frac{M}{N}(1 - \frac{M}{N})･\frac{N-n}{N-1}$$	$$\frac{(n+1)(M+1)}{N+2}$$	―	N個からなる２グループ（M個、N－M個）から、n個を取り出す（非復元抽出） ときに、M個の中から取り出される数の確立分布
ポアソン分布	$$Po(λ)=\frac{e^{-λ}･λ^x}{x!}$$	$$λ$$	$$λ$$	$$(λ以下の最大の整数)$$	$$e^{λ(s-1)}$$	ある期間に平均λ回起こる現象が、ある期間にx回起きる確率の分布 $$λ=np$$
幾何分布	$$Geo(p)=pq^x$$	$$\frac{q}{p}$$	$$\frac{q}{p^2}$$	$$0$$	$$\frac{p}{1-qs}$$	ベルヌーイを繰り返してx回失敗しx+1回目で成功
負の２項分布	$$NB(r, p)=\hspace{2mm} _rH_x･p^r･q^x$$	$$\frac{rq}{p}$$	$$\frac{rq}{p^2}$$	―	$$(\frac{p}{1-qs})^r$$	成功確立pの独立なベルヌーイ試行を繰り返し行い、r回目の成功が起こった時点でそれまでの失敗回数Yの分布$$_rH_x \hspace{2mm}=\hspace{2mm} _{x+r-1}C_x$$
多項分布	$$M(n;p_1,…,p_K)=$$ $$ \frac{n!}{y^{(1)}!…y^{(K)}!}\hspace{2mm}p_1^{y(1)}+..+p_K^{y(K)} $$	$$np_j$$	$$np_j(1 - p_j) $$	―	$$(p_1s_1+…+p_ks_k)^n$$
連続一様分布	$$U(a, b)=\frac{1}{b - a}$$	$$\frac{a + b}{2}$$	$$\frac{(b - a)^2}{12}$$	全ての値	$$\frac{e^{bt} - e^{at}}{(b - a)t}$$
正規分布	$$N(μ, σ^2)=\frac{1}{\sqrt{2π}\hspace{1mm}σ}･exp(- \frac{(x - μ)^2}{2σ^2})$$	$$μ$$	$$σ^2$$	$$μ$$	$$exp(μt + \frac{1}{2}σ^2t^2)$$
指数分布	$$Exp(λ）=λe^{-λt}$$	$$\frac{1}{λ}$$	$$\frac{1}{λ^2}$$	$$0$$	$$\frac{λ}{λ- t}$$	母数λのポアソン分布に従う確率事象が初めて観察されるまでの時間T。ポアソン分布である期間に起こる回数x=1として、変数を時間を表すtで表したもの。　また、ガンマ分布で事象aが起こる回数をa=1としたもの。 $$= G_a(1,\frac{1}{λ})$$
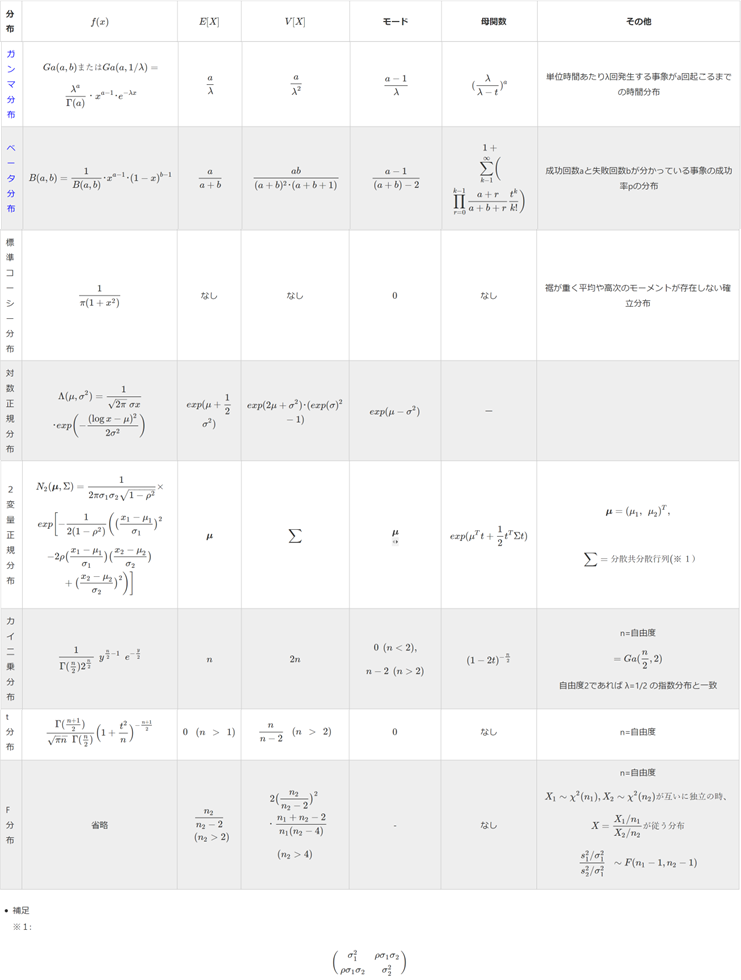
ガンマ分布	$$Ga(a, b)またはGa(a,1/λ)=$$ $$\frac{λ^a}{Γ(a)}・x^{a - 1}･e^{-λx}$$	$$\frac{a}{λ}$$	$$\frac{a}{λ^2}$$	$$\frac{a - 1}{λ}$$	$$(\frac{λ}{λ- t})^a$$	単位時間あたりλ回発生する事象がa回起こるまでの時間分布、 正の実数 x $\in \mathbb{R}^+ $を生成してくれる確率分布
ベータ分布	$$Be(a, b)=\frac{1}{B(a, b)}･x^{a - 1}･(1 - x)^{b - 1}$$	$$\frac{a}{a + b}$$	$$\frac{ab}{(a + b)^2･(a + b + 1)}$$	$$\frac{a - 1}{(a + b) - 2}$$	$$1 + \sum_{k-1}^{\infty}\biggl(\prod_{r=0}^{k-1} \frac{a+r}{a+b+r} \frac{t^k}{k!}\biggr) $$	成功回数aと失敗回数bが分かっている事象の成功率pの分布。 x $\in$ (0, 1)となるような変数を生成してくれる確率分布。形状が非常に柔軟であるため、事前確率分布として扱いやすいのでベイス統計において重要な役割を持つ確率分布。$$ \alpha = \beta = 1 の場合は標準一様分布(平均値 = 最頻値)になる。$$ $$\alpha = \beta >1の場合は正規分布（平均値 = 最頻値）になる。 $$ $$ \alpha > \beta の場合は右肩上がりのグラフ（最頻値が平均値より右側）になる。$$ $$ \alpha < \betaの場合は左肩上がりのグラフ（平均値が最頻値より右側）になる。$$
標準コーシー分布	$$\frac{1}{π(1 + x^2)} $$	なし	なし	$$0$$	なし	裾が重く平均や高次のモーメントが存在しない確立分布
対数正規分布	$$Λ(μ, σ^2)=\frac{1}{\sqrt{2π}\hspace{1mm}σx}･exp\biggl(- \frac{(\log x - μ)^2}{2σ^2}\biggr) $$	$$exp(μ + \frac{1}{2}σ^2)$$	$$exp(2μ + σ^2)･(exp(σ)^2 - 1)$$	$$exp(μ - σ^2) $$	ー
２変量正規分布	$$N_2(\boldsymbol{\mu}, \boldsymbol{Σ})=\frac{1}{2πσ_1σ_2\sqrt{1-ρ^2}}×$$ $$exp\biggl[-\frac{1}{2(1 - ρ^2)}\biggl(\bigl(\frac{x_1 - μ_1}{σ_1}\bigr)^2 $$ $$- 2ρ\bigl(\frac{x_1 - μ_1}{σ_1}\bigr)\bigl(\frac{x_2 - μ_2}{σ_2}\bigr) + \bigl(\frac{x_2 - μ_2}{σ_2}\bigr)^2 \biggr) \biggr] $$	$$ \boldsymbol{\mu} $$	$$\boldsymbol{\sum}$$	$$ \boldsymbol{\mu} $$	$$ exp(μ^Tt + \frac{1}{2}t^TΣt) $$	$$\boldsymbol{\mu} = (μ_1,\hspace{2mm}μ_2)^T, $$ $$\hspace{4mm}\boldsymbol{\sum} = 分散共分散行列(※１） $$
カイ二乗分布	$$\frac{1}{Γ(\frac{n}{2})2^{\frac{n}{2}}}\hspace{2mm}y^{\frac{n}{2}-1}\hspace{2mm}e^{-\frac{y}{2}}$$	$$n$$	$$2n$$	$$0 \hspace{2mm}(n<2),$$ $$ n - 2 \hspace{2mm}(n > 2)$$	$$(1 - 2t)^{-\frac{n}{2}}$$	$$=Ga(\frac{n}{2}, 2), \hspace{5mm} n=自由度$$ $$ \chi^2値 \hspace{5mm}=\hspace{5mm} \sum_{i=1}^k \frac{(観測度数_i - 期待度数_i)^2}{\hspace{15mm}期待度数_i\hspace{15mm}}　であり、$$　 $$ \chi^2値がとる相対度数（確率密度）の分布が\chi^2分布。 $$ 自由度2であれば λ=1/2 の指数分布と一致、自由度が大きくなると正規分布に近づく
t分布	$$\frac{Γ(\frac{n+1}{2})}{\sqrt{πn}\hspace{2mm}Γ(\frac{n}{2})} \Bigl(1 + \frac{t^2}{n}\Bigr)^{-\frac{n+1}{2}}$$	$$0 \hspace{4mm}(n\hspace{2mm}>\hspace{2mm} 1)$$	$$\frac{n}{n -2} \hspace{4mm}(n\hspace{2mm}>\hspace{2mm}2) $$	$$0$$	なし	n=自由度
F分布	省略	$$\frac{n_2}{n_2 - 2} \hspace{2mm} (n_2 > 2)$$	$$2\bigl(\frac{n_2}{n_2 - 2}\bigr)^2\hspace{1mm}・\frac{n_1+n_2-2}{n_1(n_2-4)} $$ $$(n_2 > 4) $$	-	なし	n=自由度 $$ X_1 \sim χ^2(n_1), X_2 \sim χ^2(n_2)が互いに独立の時、$$ $$X= \frac{X_1/n_1}{X_2/n_2}が従う分布 $$ $$ \frac{s_1^2/σ_1^2}{s_2^2/σ_1^2} \hspace{3mm}\sim F(n_1-1, n_2-1)$$

• 補足
  ※１:

\begin{pmatrix}
σ_1^2 & ρσ_1σ_2 \\
ρσ_1σ_2 & σ_2^2
\end{pmatrix}

【補足】横スクロールなしにみえるように画像でも掲載します(解像度は悪く多少見えにくいですがご了承ください）

---

統計検定２級向けにチートシートを記載しています。
よろしかったらこちらもご参照ください。