UUB (Uniformly Ultimately Bounded) について

論文を読んでいて，UUB (Uniformly Ultimately Bounded) という有界性の指標が出てきたので勉強して理解したことをメモします．

UUBの定義

$\exists{b, c}>0, a\in(0,c)$ とし，初期時刻 $t_0$ に依存しない $T=T(a,b)$ を用いて以下が成立するとき， $x$ はUUBであるという．
$$\parallel{x(t_0)\parallel}\leq{a}\Rightarrow\parallel{x(t)\parallel}\leq{b},\quad\forall{t}\geq{t_0+T}$$

UUBのイメージ

Uniformly（一様に：初期時刻に非依存）+ Ultimately（最終的に：あるタイミングから（初めからである必要なし））+ Bounded（有界）

完全に0に収束するわけではないが，有限時間である0の近傍の領域内に収まりそこから永遠に抜け出すことはないというイメージ
（もし領域外に出ても，領域外では変数はノルムが単調減少する方向に変化するため，また領域内に入る）

注）

• $a<b$ のとき "uniformly bounded"（初めから満たしているので）
• $a$ が十分大きいと "globally" がつく
  • "globally" uniformly bounded
  • "globally" uniformly ultimately bounded

UUBの具体例

次のノンオートノマス（ $\dot{x}=f(x,t)$において $f$ が $t$ の陽なる関数）な非線形システムの初期値問題を考える．

$$\dot{x}=-x+\delta \sin t, \quad x\left(t_{0}\right)=a>\delta>0$$

（このシステムは平衡点を持たない．）
リアプノフ関数 $V$ を次のようにおく．

$$V(x)=\frac{x^2}{2}$$

$t$ で微分すると

$$\dot{V}(x)=x \dot{x}=x(-x+\delta \sin t)=-x^{2}+\delta x \sin t \leq-x^{2}+\delta|x|=-|x|(|x|-\delta)$$

以上より

$$\dot{V}(x)<0, \quad \forall|x|>\delta$$

よって，領域 $B_\delta=\lbrace|x|\leq\delta\rbrace$ の外では $\dot{V}<0$となる．

ここで， $V$ は $x$ に関する最小値0の凸関数なので， $\dot{V}<0$ のとき $x$ は $|x|$ の値が減少する方向に単調に変化する．

すなわち，$x$ の初期値が $B_\delta$ の外にあった場合も有限時間で $B_\delta$ の内部に入り，以降 $B_\delta$ 内に留まり続ける．← (globally) UUB

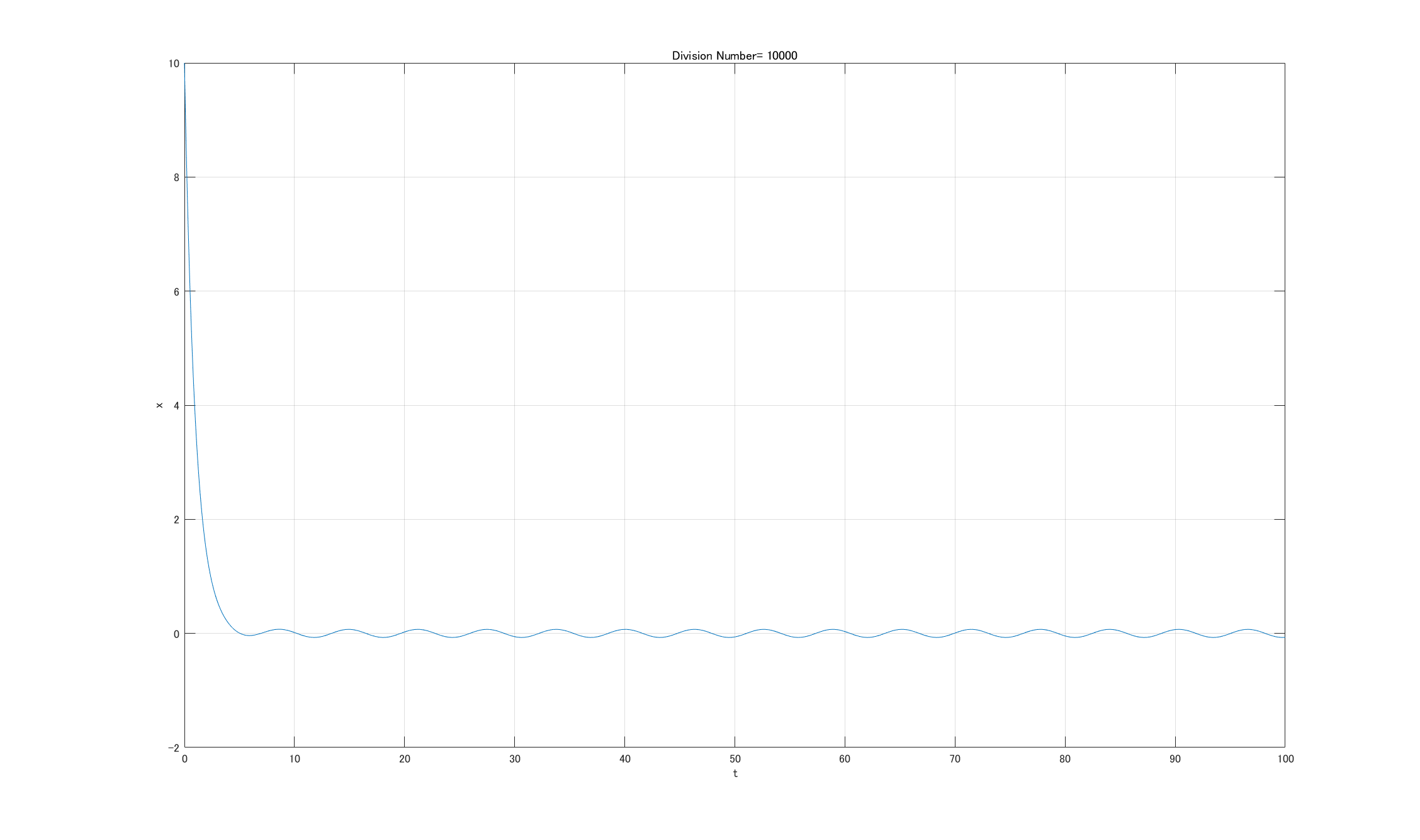
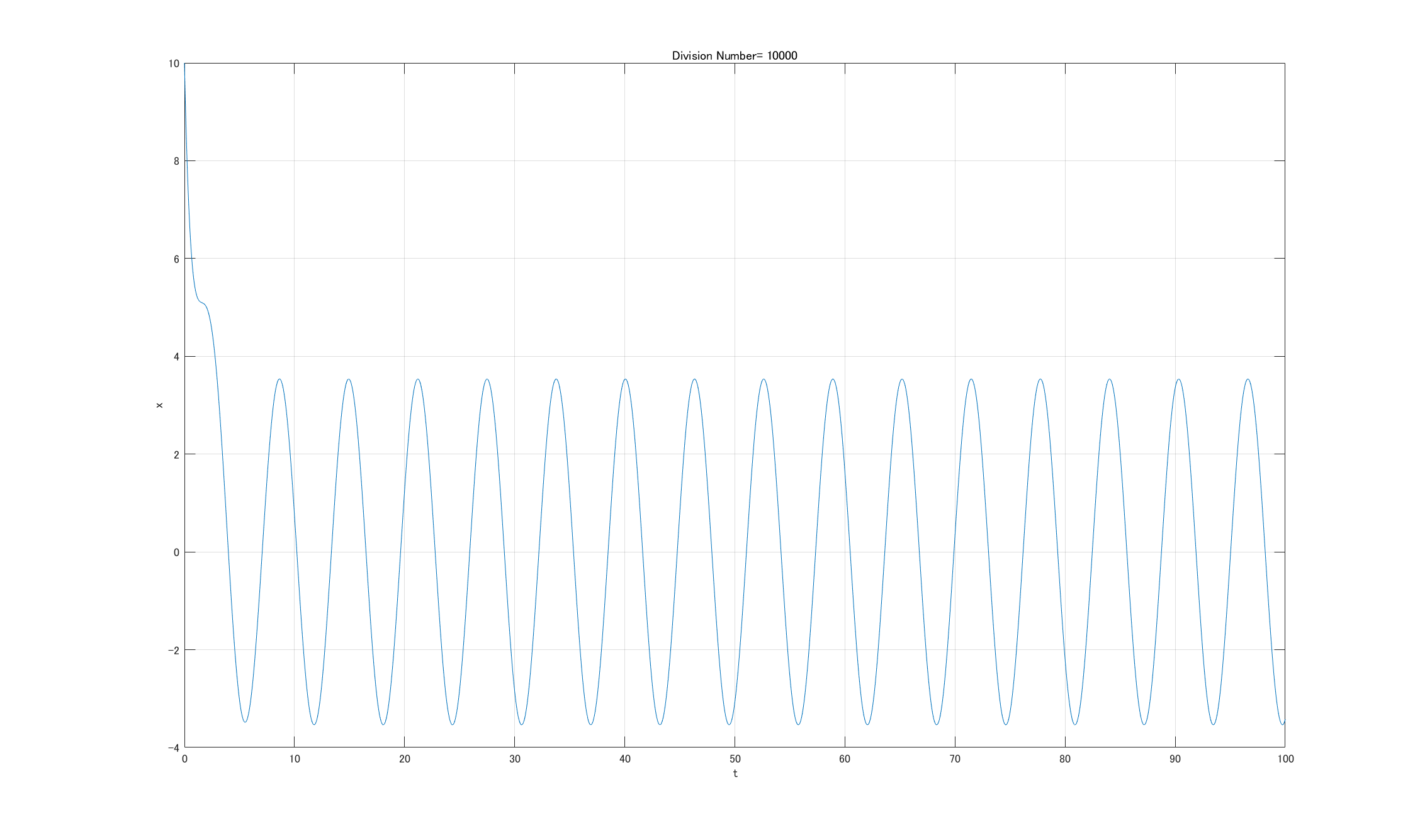
実際MATLABで描画すると確かにglobally UUBである．

• $\delta=0.1,\quad x_0=10$

• $\delta=5,\quad x_0=10$

コード

4次ルンゲクッタによる数値計算のコード

solver.m

clear
syms t x(t);

d = 5;
t0=0;x0=10;te=100;n=10001;
t=linspace(t0,te,n);
x=zeros(1,n);
dt=(te-t0)/(n-1);
x(1)=x0;
for k=2:n
    k1=f(x(k-1),t(k-1),d);
    k2=f(x(k-1)+dt/2*k1,t(k-1)+dt/2,d);
    k3=f(x(k-1)+dt/2*k2,t(k-1)+dt/2,d);
    k4=f(x(k-1)+dt*k3,t(k-1)+dt,d);
    x(k)=x(k-1)+(k1+2*k2+2*k3+k4)/6*dt;
end
plot(t,x,'-');grid('on');
title(['Division Number= ',num2str(n-1)]);
xlabel('t');ylabel('x');

function dx = f(x,t,d) 
    dx = -x + d * sin(t);
end

リアプノフの安定性解析を用いたUUBの示し方

• リアプノフ関数 $V$ を，UUBを示したい変数 $x$ に関する凸関数 $V(x)$ として定義
• $\dot{V}(x)<0$ を $x$ に関するpositive definite function（ノルム等）で上から抑えることで証明（成立条件付き可）

リアプノフの意味の安定 (SISL¹)とUUBの違い

• SISLは平衡点近傍で留まり続けることを保証するが，UUBは平衡点は無関係
  • UUBは単純に有界性を示すのみ
• SISLは平衡点近傍からスタートして平衡点近傍で留まり続けることを示さなければならず，これは未知の外乱等が存在する実機ではかなり厳しい要件
• UUBは平衡点や原点近傍からスタートする必要がない
  • UUBはSISLより"甘い"が実用的

参考文献

• http://www.cds.caltech.edu/archive/help/uploads/wiki/files/218/CDS270-I_Lecture2.pdf

1. Stable In the Sense of Lyapnov ↩