目標
標準正規分布の四分位範囲の導出
よく統計学の本の付録についてる「標準正規分布表」の数値の厳密な計算方法
計算手順
とりあえず、第1四分位数を$Q_1$, 第3四分位数を$Q_3$とおくと、 標準正規分布の確率密度関数である
$$ f(x)= \frac{1}{\sqrt{2\pi}}exp\left(-\frac{x^2}{2}\right)$$
に対して、以下の関係が成り立ちます。
$$\int_{-\infty}^{Q_1} f(x) \ dx=\frac{1}{4}$$
$$\int_{-\infty}^{Q_3} f(x) \ dx=\frac{3}{4}$$
そしてこの2式の差をとると、
\begin{align}
\int_{-\infty}^{Q_3} f(x) \ dx-\int_{-\infty}^{Q_1} f(x) \ dx&=\int_{Q_1}^{Q_3} f(x) \ dx \\
&=\frac{1}{2}
\end{align}
ここで、 標準正規分布であるので、 平均$\mu=0$が成立します。 定数cを用いて、
$$Q_1=\mu-c=-c$$
$$Q_3=\mu+c=c$$
と表現できるので
\begin{align}
\int_{Q_1}^{Q_3} f(x) \ dx&=\int_{-c}^{c} f(x) \ dx\\ &=\frac{1}{2}
\end{align}
になります。
ここで、誤差関数erf$(x)$を用いて、
\begin{align}
\int_{-c}^{c} exp\left(-\frac{x^2}{2}\right) \ dx&=\left[\frac{\pi}{2} erf\left(\frac{x}{\sqrt{2}}\right)\right]_{-c}^{c}\\
&= \sqrt{2\pi} erf\left(\frac{c}{\sqrt{2}}\right)
\end{align}
と表されます(Wolfram Alphaさん、ありがとう)ので、以下の等式が成り立ちます。
$$erf\left(\frac{c}{\sqrt{2}}\right)=\frac{1}{2}$$
ここで誤差関数に含まれるcを求めたいのですが、部分積分などの解析アプローチでは全く歯が立ちません。ここで積分の沼にはまるわけです。どのような方針で求めましょうか。
誤差関数に関する等式をプログラムで
今回はNumpyをモジュールとして使用します。
幸いなことにnumpyには誤差関数が既に組み込まれているのでめっちゃ楽にかけます。
(Scipyでも同様に出来るみたいです。)
あとで関数の可視化もするのでmatplotlibも入れときます。
import numpy as np
import matplotlib.pyplot as plt
さて、ここから下記の等式が成り立つ$c$を求めようと思います。$$erf\left(\frac{c}{\sqrt{2}}\right)=\frac{1}{2}$$
ところでこの誤差関数は
$$erf(x)=\frac{2}{\sqrt{\pi}}\int_{0}^{x}exp\left(-t^2\right)dt$$
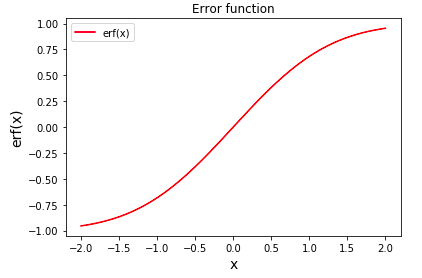
という形で表されます。この誤差関数がどのような関数形か可視化してみると
fig = plt.figure(figsize = (6, 4))
ax = fig.add_subplot(111)
x=np.linspace(-2.0,2.0,2000000)
y=np.erf(x/np.sqrt(2))
ax.set_xlabel("x", fontsize = 14)
ax.set_ylabel("erf(x)", fontsize = 14)
plt.plot(x, y, ls="-", label="erf(x)", color="red")
plt.title("Error function")
plt.legend()
plt.show()
<出力結果>
Sigmoid関数みたいな概形で、狭義単調増加してますね。
ということで、以下のようなアプローチでcを解きます。
①
標準正規分布なので標準偏差の特徴(USE OF STANDARD DEVIATION)からcの範囲を[-1,1]とし、分布表のオーダーに倣って$ 10^{-6} $ずつ増加させていきます。
②$ erf (\frac{c}{\sqrt{2}}) <\frac{1}{2} $ 未満となる間は計算を実行させ、積分値を増加させていき、$ erf (\frac{c}{\sqrt{2}}) ≒ \frac{1}{2} $となるギリギリの値cを求める。
これを誤差関数のプログラムのときと同様にコーディングする。
for c in np.arange(-1.000000,1.000000):
while np.erf(c/np.sqrt(2)) < 1/2:
c=c+0.000001
break
print(c)
<出力結果>
0.6744900000064764
可視化も実行してみると、
fig = plt.figure(figsize = (6, 4))
ax = fig.add_subplot(111)
x=np.linspace(-1.0,1.0,1000000)
y=np.erf(x/np.sqrt(2))
ax.set_xlabel("c", fontsize = 14)
ax.set_ylabel("erf score", fontsize = 14)
plt.plot(x, y, ls="-", label="erf(c/√2)")
ax.axhline(0.5, ls = "-.", color = "green", label="erf score = 1/2")
plt.title("Error function")
plt.legend()
plt.show()
<出力結果>
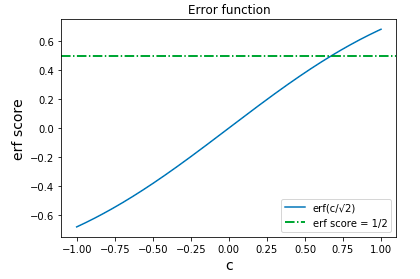
2つの線の交点のcの値が、先程の出力結果の0.67449...に対応しています。
ラスト
プログラム結果から, $c=0.674490$...となるので、 四分位範囲は
\begin{align}
c-(-c)&=2c \\
&= 2*(0.674490...) \\
&≒ 1.349
\end{align}
よって、 標準正規分布の四分位範囲は$1.349$と求まります。
[2022/01/17 16:45 追記]
現在はPythonのscipyパッケージのspecialによって、下記のように簡単に誤差関数をかけるので上記のような大袈裟な分割は必要ありません。
from scipy import special
import matplotlib.pyplot as plt
x = np.linspace(-1.00, 1.00)
plt.plot(x, special.erf(x))
plt.xlabel('x')
plt.ylabel('erf(x)')
plt.show()