はじめに
初めまして、ようこそお越しくださいました!
現象数理学科2年生の分際ながら初記事を書かせていただきます。
とは言ってもコードを書くわけではなく自然現象に関する「何か」を書きます。
今回はSchrödinger方程式を使い、波動関数を紹介いたします。
そもそもSchrödinger方程式って
自然界には原子という存在があります。元素の最小単位です。
20世紀を迎えるまでは古典力学と言われるマクロな力学が主流でした。
ところがミクロな粒子の運動について考えようと思うと古典力学では説明できない事柄も現れたので、新しい分野である量子力学が登場しました。
量子力学はミクロな現象を研究することでマクロな現象も扱うことができます。
ではここで水素原子について取り上げてみます。
Bohrによって導かれた水素原子モデル
$
・2πr=nλ\
・rp=\frac{nh}{2π} (角運動量)\
(r:電子が描く円軌道の半径, λ:波長, h:プランク定数, n:量子数)
$
を用いた水素原子のスペクトルの値はとびとびの値をとりますが、これが全ての原子に当てはまるのかというとそうではなく原子によって結果にズレが生じます。
そこで他の粒子にも対応できるようにSchrödinger方程式が生まれました。
では具体的にどのような式になるのか導出方法とともに見ていきましょう。
原子の物質波を定常波で考えると境界条件より両端が振幅0の節になっているので
$
A(x)=A_0sin(\frac{nπ}{L}x)\
(A_0:振幅, L:波長)\
$
という波の式になります。
この両辺を2回微分すると
$
\frac{d^2}{dx^2}A(x)=-(\frac{2π}{λ})^2 A(x)...(*)\
$
ポテンシャル井戸の中に電子が伴うと考えると場所rにおける振幅をφ(r)とおくと、エネルギー保存則よりEを粒子の持つ全エネルギー、Vを粒子のポテンシャルエネルギーとして
$
E-V(r)=\frac{h^2}{2mλ^2}\
$
が成り立つので
$
(*)⇔\frac{d^2}{dx^2}φ(x)=-(\frac{2π}{λ})^2 φ(x)$
つまり$(*)=-\frac{8mπ^2}{h^2}(E-V(x))φ(x)
$
これを整理して
-\frac{h^2}{8mπ^2}\frac{d^2}{dx^2}φ(x)+V(x)φ(x)=Eφ(x)\\
これを1次元のSchrödinger方程式と呼ぶ。
一般の3次元の場合は微分を3次元をのものに置き換え粒子の位置ベクトルをrとして
-\frac{h^2}{8mπ^2}(\frac{∂^2}{∂x^2}+\frac{∂^2}{∂y^2}+\frac{∂^2}{∂z^2})φ(r)+V(r)φ(r)=Eφ(r)\\
というふうに表現できる。
この式からもわかるようにSchrödinger方程式というのは
ポテンシャルの形V(r)を波動関数φ(r)に変換する装置なのです!
波動関数の構築
ある原子に対して波動関数を作るにはどんな要素が必要かを考えてみましょう。
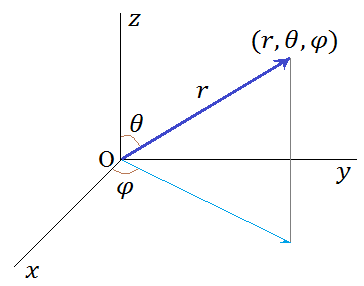
原子核を中心として電子の極座標をγ(r,θ,φ)とおく。
rの変化→電子が原子核に近づいたりと遠ざかったりする運動...(a)
(θ,φ)の変化→原子核まわりの回転運動...(b)
この3つの自由度に対して3つの量子数が決まる。
(1)原子核に対する遠近運動はrの変わらない円運動を考えると軌道面は傾いている。
この運動に対してSchrödinger方程式を解くと回転運動の角運動量は量子数lを用いて
$
\sqrt{l(l+1)}\frac{h}{2π}...(I)
$
と表現される。
(2)この回転運動をxy平面に投影してφによってのみ変わるz軸周りの運動を考える。
Bohrのモデルから角運動量のz軸への投影が整数mを用いて
$
\frac{mh}{2π}\
$
とならなければならない。
この時、x,y成分によって角運動量は変化しないので(I)から$m=-l,-l+1,...,l-1,l$の値をとる。
この回転運動の波動関数を$Y_{lm}(θ,φ)$と表すことにする。
(3)次に原子核に近づいたり遠ざかったりする運動を考える。電子が回転している時の遠心力の大きさはlによって決まる。ここでlは非負整数である必要がある。それを解決するためにあるlが指定された時の遠近運動は量子数をj(自然数)としてn=j+lと表現するとn(自然数)に対してlは非負整数で考えることができる。
この表現の仕方を動径波動関数$R_{nl}$と言ったりする。
まとめとして回転運動と遠近運動の両方を含む波動関数を
$\psi_{nlm}(r)$=$R_{nl}・Y_{lm}(θ,φ)
$
と表す。
電子の存在確率
最後に半径rの球上に電子が存在する確率を求めよう。
半径$r$の球と半径$r+dr$($dr$は微小距離)の球を考えると厚みは$dr$で、($θ,φ$)を中心に$dθ,dr$だけ変化すると考えると、この厚みでの動きは各々$rdθ$と$rsinθdφ$となる。
よって、規格化された$φ(r)$に対してこの厚みに電子が存在する確率は
$\int_{0}^{2π}\int_{0}^{π}|φ(r)|^2r^2drsinθdθdφ\
=r^2(R_{nl}(r))^2[\int_{0}^{2π}\int_{0}^{π}Y_{lm}(θ,φ)sinθdθdφ]^2dr\
=r^2(R_{nl}(r))^2dr\
=D_{nl}(r)dr$\
$D_{nl}(r)$は動径分布関数と呼ばれ、単位厚みあたりの粒子の存在確率に値する。そしてこの式からrの値として最も確率が大きい値はBohrの半径と一致することがわかる。