はじめてのQuantum Walk

はじめに

去年度に引き続き、Advent Calendarを執筆させていただきます。

2017年度版では確率積分について記述しましたが、今年は「量子ウォーク」について。

量子ウォークは量子コンピューターの理論を整備する上で役立つ数理モデルです。
難しい知識は必要ありません。順を追ってゆっくり見ていきましょう。

(この内容は去年度の実験データ解析演習の最終レポートで書いた内容です。)

準備知識

とりあえず本題に入る前に必要な知識は次の2つ

1, Unitary行列
2, Random Walk

順番に見ていきましょう。

1, Unitary行列

$ A $がUnitary行列
⇔$ A $の共役転置行列$ A' $に対して、$ AA'=A'A=I $ (単位行列) が成立

Ex:
以下の行列はUnitary行列になります。

A=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} 
\end{pmatrix}

実際確かめてみると

AA'=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} 
\end{pmatrix}*
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} 
\end{pmatrix}=
\begin{pmatrix}
1 & 0 \\
0 & 1 
\end{pmatrix}

A'A=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} 
\end{pmatrix}*
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} 
\end{pmatrix}=
\begin{pmatrix}
1 & 0 \\
0 & 1 
\end{pmatrix}

となります。ここでいう「行列」は複素数$ \mathbb{C} $を要素に取ります。

2, Random Walk

ここでは簡単に1次元のRandom Walkを紹介しましょう。
現在いる位置に対して右に移る確率を$ p \in [0,1] $ 、左に移る確率を$ 1-p $として移動の軌跡を追う数理モデルのことを指します。

<標準型の量子ウォーク>

さて、準備もできましたので1次元格子上の量子ウォークに入りましょう。

まず、量子ウォークを理解するためには"3つの概念"が必要になります。

1, 確率振幅ベクトル
2, 時間発展ルール
3, 確率

解説をしていきましょう。

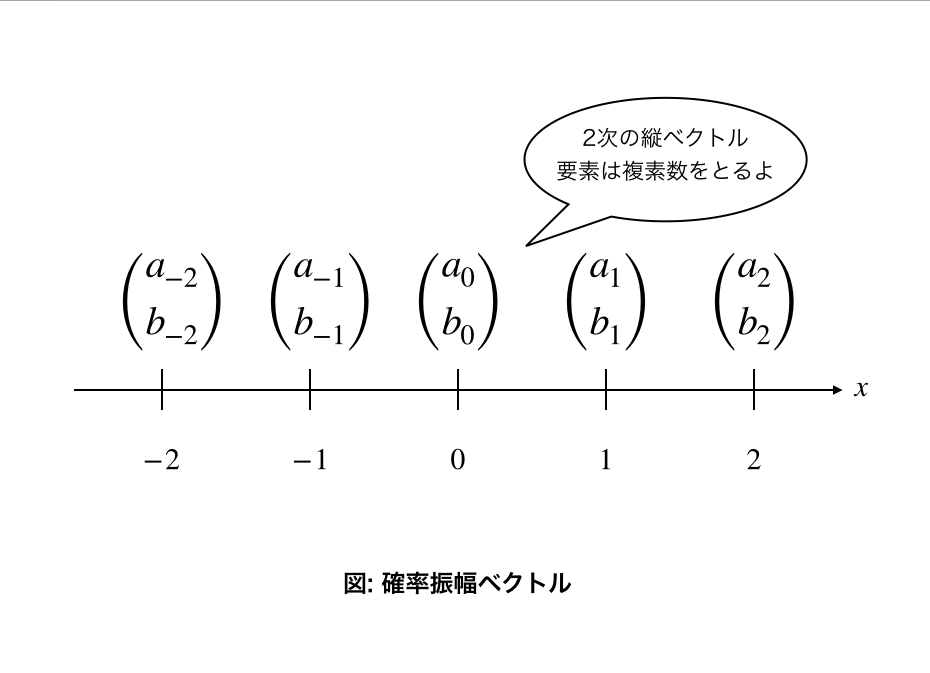
1, 確率振幅ベクトル
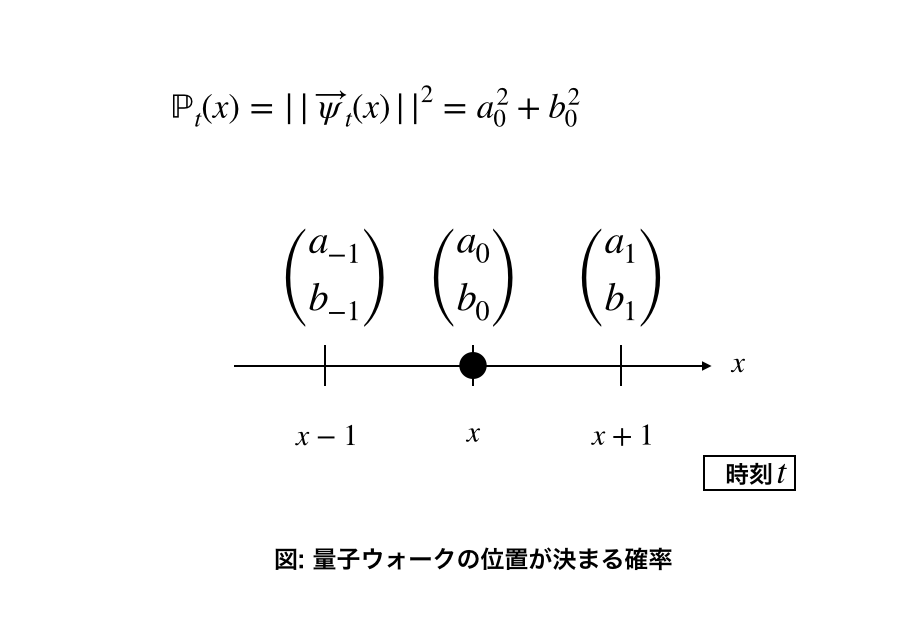
n次元格子状の各場所に、2つの複素数を成分にもつ縦ベクトルです。

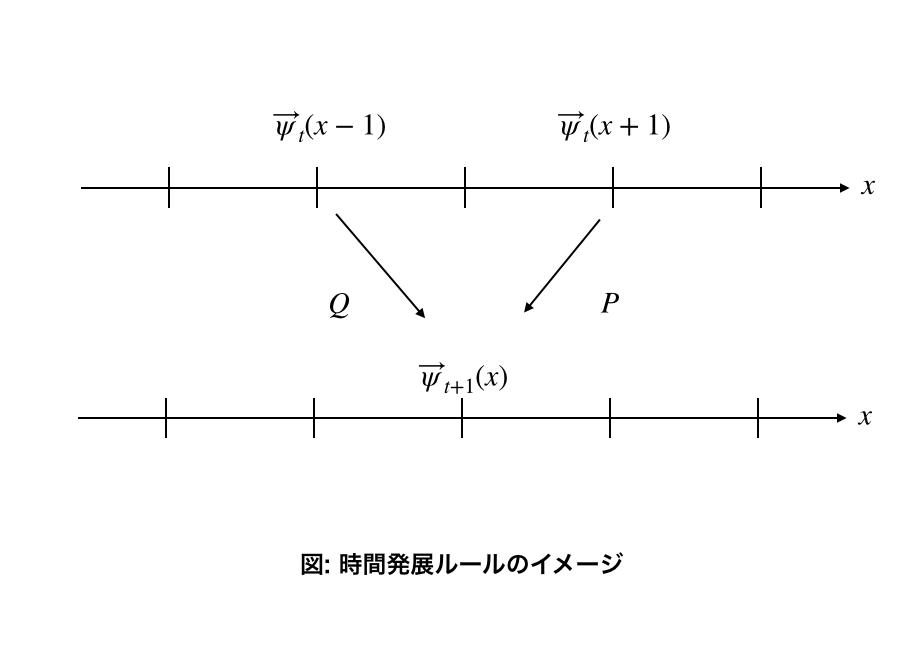
2, 時間発展ルール
確率振幅ベクトルの時間発展のことです。
全ての場所に初期確率振幅ベクトルを設定した後、あるルールに従って確率振幅ベクトルが時間発展します。

初期確率振幅ベクトルが与えられた時刻を0とし、その後$ t $回時間発展させたときの場所$ x $での確率振幅ベクトルを$ \vec{\psi}_t(x) $とします。

量子ウォークの時間発展の式は以下のような形になります。
$\vec{\psi}_{t+1}(x) = P\vec{\psi} _t(x+1)+Q\vec{\psi} _t(x-1)$

※P=
\begin{pmatrix}
a & b \\
0 & 0 
\end{pmatrix}
\qquad
Q=
\begin{pmatrix}
0 & 0 \\
c & d 
\end{pmatrix}

3, 確率
時刻$t$において場所$x$に量子ウォーカーの位置が決まる確率$\mathbb{P}_t(x)$は

$\mathbb{P}_t(x)=||\vec{\psi} _{t}(x)||^2$ $\quad$ で定義されます。

<Point>

◎ 初期確率振幅ベクトルの設定制限

$\quad \sum_{x=-\infty}^{\infty} ||\vec{\psi} _{0}(x)||^2=1$ $\quad$が成立することが必要条件。

◎ P+QがUnitary行列であること

$\quad$ この仮定によって任意の時刻$t$に対して
$\quad \sum_{x=-\infty}^{\infty} ||\vec{\psi} _{t}(x)||^2=1$ $\quad$となっていることが結果からわかる。

⭐︎具体的に例でやってみましょう

Ex:

※P=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 
\end{pmatrix}
\qquad
Q=
\begin{pmatrix}
0 & 0 \\
\frac{1}{\sqrt{2}} &  -\frac{1}{\sqrt{2}}
\end{pmatrix}

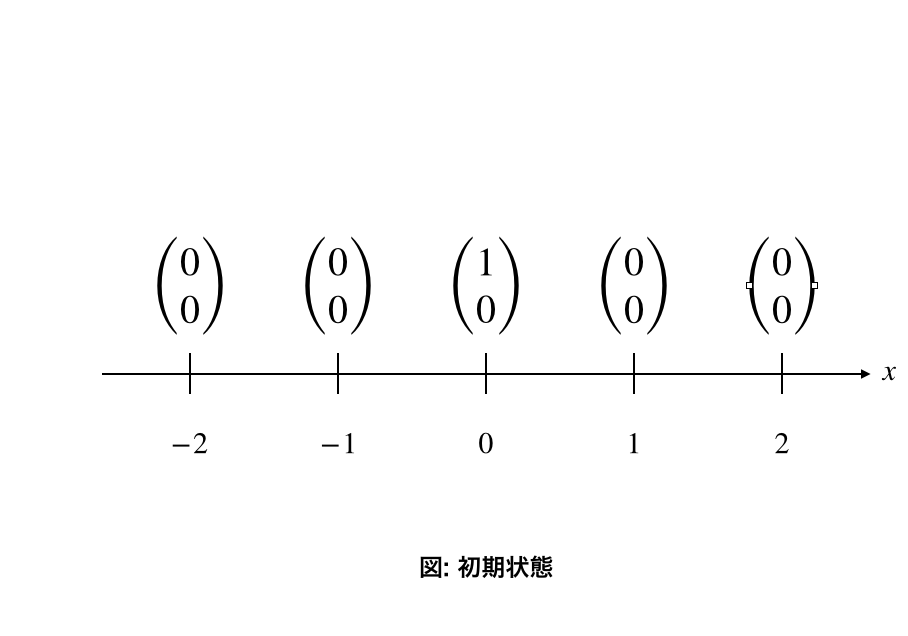
初期確率振幅ベクトルを以下のようにとってみます。

※\vec{\psi} _{0}(0)=
\begin{pmatrix}
1\\
0  
\end{pmatrix}
\qquad
\vec{\psi} _{0}(x)=
\begin{pmatrix}
0\\
0  
\end{pmatrix}
\quad
(x \neq 0)

まずは各時刻に対して確率振幅ベクトルを計算してみましょう。

・時刻$t=1$のとき
$\vec{\psi}_{1}(-1) = P\vec{\psi} _0(0)+Q\vec{\psi} _0(-2)=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 \\
\end{pmatrix}*
$$
\begin{pmatrix}
1 \\
0
\end{pmatrix}+
\begin{pmatrix}
0 & 0 \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}
= \begin{pmatrix}
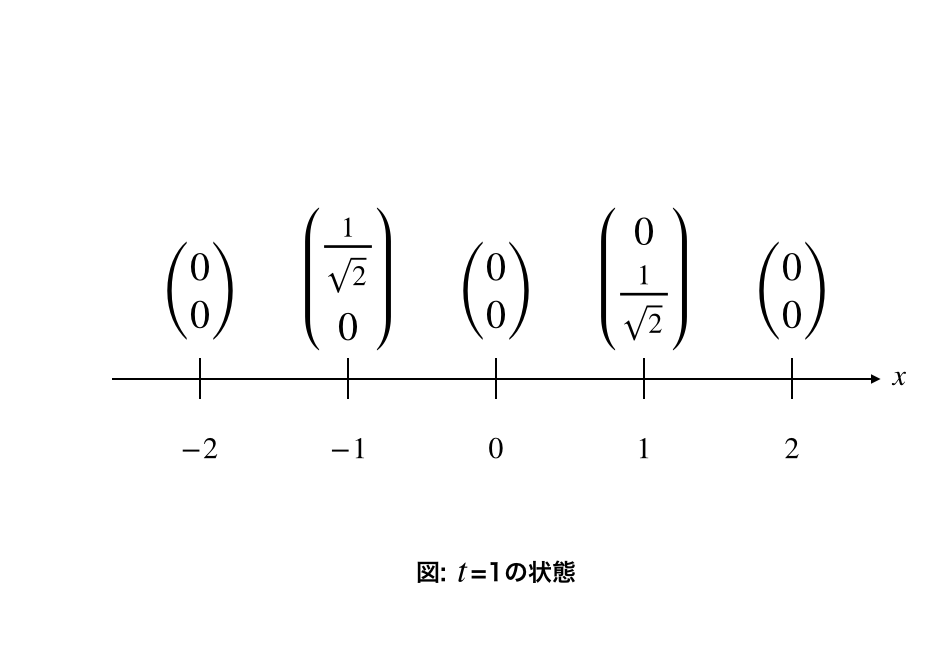
\frac{1}{\sqrt{2}} \\
0
\end{pmatrix}$

$\vec{\psi}_{1}(0) = P\vec{\psi} _0(1)+Q\vec{\psi} _0(-1)=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}+
\begin{pmatrix}
0 & 0 \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}
= \begin{pmatrix}
0 \\
0
\end{pmatrix}$

$\vec{\psi}_{1}(1) = P\vec{\psi} _0(2)+Q\vec{\psi} _0(0)=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}+
\begin{pmatrix}
0 & 0 \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{pmatrix}*
$$
\begin{pmatrix}
1 \\
0
\end{pmatrix}
= \begin{pmatrix}
0 \\
\frac{1}{\sqrt{2}}
\end{pmatrix}$

$t=1$では以下のような図になります。

・時刻$t=2$のとき
$\vec{\psi}_{2}(-1) = P\vec{\psi} _1(0)+Q\vec{\psi} _1(-2)=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}+
\begin{pmatrix}
0 & 0 \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}
= \begin{pmatrix}
0 \\
0
\end{pmatrix}$

$\vec{\psi}_{2}(0) = P\vec{\psi} _1(1)+Q\vec{\psi} _1(-1)=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
\frac{1}{\sqrt{2}}
\end{pmatrix}+
\begin{pmatrix}
0 & 0 \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{pmatrix}*
$$
\begin{pmatrix}
\frac{1}{\sqrt{2}} \\
0
\end{pmatrix}
= \begin{pmatrix}
\frac{1}{2} \\
\frac{1}{2}
\end{pmatrix}$

$\vec{\psi}_{2}(1) = P\vec{\psi} _1(2)+Q\vec{\psi} _1(0)=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}+
\begin{pmatrix}
0 & 0 \\
\frac{1}{\sqrt{2}} & -\frac{1}{\sqrt{2}} \\
\end{pmatrix}*
$$
\begin{pmatrix}
0 \\
0
\end{pmatrix}
= \begin{pmatrix}
0 \\
0
\end{pmatrix}$

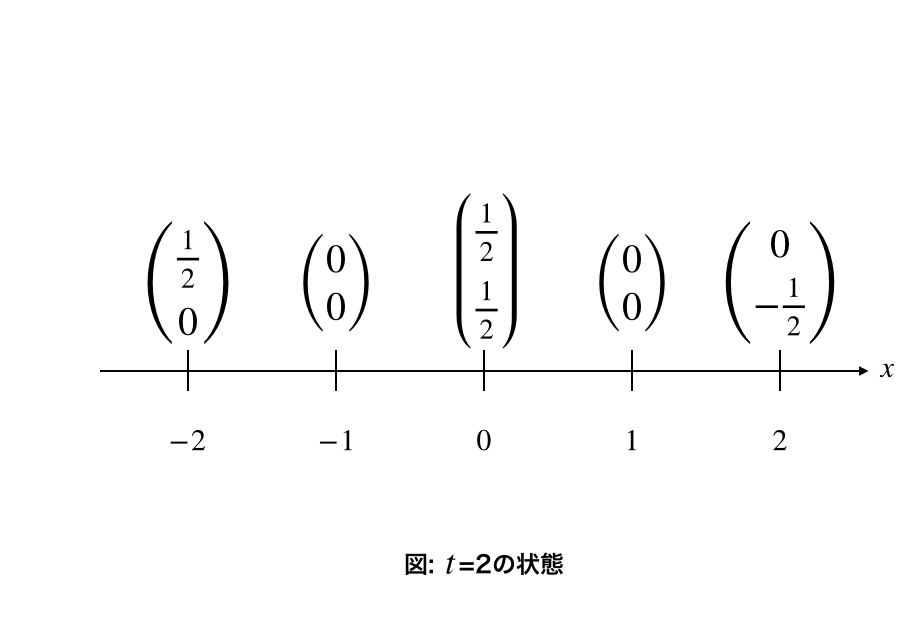
$t=2$では以下のような図になります。

次に、各時刻に対して量子ウォーカーの位置が決まる確率を計算します。

・時刻$t=1$
$\qquad$ $\mathbb{P}_1(-1)=||\vec{\psi} _{1}(-1)||^2=\Biggl|\Biggl|$$\begin{pmatrix}
\frac{1}{\sqrt{2}} \\
0
\end{pmatrix} \Biggr|\Biggr| ^2 =\frac{1}{2}$

$\qquad$ $\mathbb{P}_1(0)=||\vec{\psi} _{1}(0)||^2=\Biggl|\Biggl|$$\begin{pmatrix}
0 \\
0
\end{pmatrix} \Biggr|\Biggr| ^2 =0$

$\qquad$ $\mathbb{P}_1(1)=||\vec{\psi} _{1}(1)||^2=\Biggl|\Biggl|$$\begin{pmatrix}
0\\
\frac{1}{\sqrt{2}}
\end{pmatrix} \Biggr|\Biggr| ^2 =\frac{1}{2}$

・時刻$t=2$
$\qquad$ $\mathbb{P}_2(-2)=||\vec{\psi} _{2}(-2)||^2=\Biggl|\Biggl|$$\begin{pmatrix}
\frac{1}{2} \\
0
\end{pmatrix} \Biggr|\Biggr| ^2 =\frac{1}{4}$

$\qquad$ $\mathbb{P}_2(0)=||\vec{\psi} _{2}(0)||^2=\Biggl|\Biggl|$$\begin{pmatrix}
\frac{1}{2} \\
\frac{1}{2}
\end{pmatrix} \Biggr|\Biggr| ^2 =\frac{1}{2}$

$\qquad$ $\mathbb{P}_2(2)=||\vec{\psi} _{2}(2)||^2=\Biggl|\Biggl|$$\begin{pmatrix}
0\\
-\frac{1}{2}
\end{pmatrix} \Biggr|\Biggr| ^2 =\frac{1}{4}$

<Check Point>
$\qquad \sum_{x=-\infty}^{\infty} ||\vec{\psi} _{0}(x)||^2=1$が成り立っていることから(全確率)=1も確認できます。

さらに時間発展ルールに基づいて進めると、確率分布は以下のようになります。

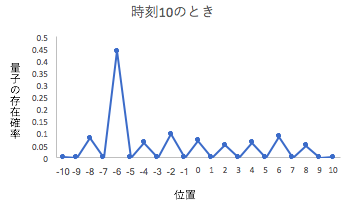
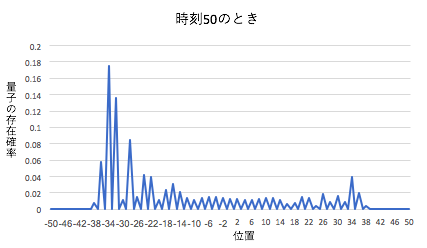
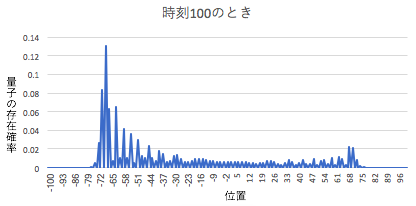
量子ウォークの発展形

上記の量子ウォークは、あくまでも基本形であり発展形がいくつか存在します。

時間依存・空間依存形

これは$P、Q$が時間や空間に依存しているパターン
例えば、時間依存形なら

(i)\quad P_1=
\begin{pmatrix}
\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \\
0 & 0 
\end{pmatrix}
\qquad
Q_1=
\begin{pmatrix}
0 & 0 \\
\frac{1}{\sqrt{2}} &  -\frac{1}{\sqrt{2}}
\end{pmatrix}\qquad
(t=0,2,4...)
\\\\
(ii)\quad P_2=
\begin{pmatrix}
0 & 1 \\
0 & 0 
\end{pmatrix}
\qquad
Q_2=
\begin{pmatrix}
0 & 0 \\
1 & 0
\end{pmatrix}\qquad
(t=1,3,5...)

といった感じでUnitary行列が時間でSwitchingします。

確率振幅ベクトルの成分が拡張されたモデル

ここまで扱ってきたモデルは確率振幅ベクトルも$P、Q$も2次の行列でしたが、この行列の次数を増やして拡張したモデルを考えることも可能です。
例えば下記のようなモデル。

P=
\begin{pmatrix}
-\frac{1}{3} & \frac{2}{3} & \frac{2}{3}\\
0 & 0 & 0\\
0 & 0 & 0
\end{pmatrix}
\qquad
Q=
\begin{pmatrix}
0 & 0 & 0\\
\frac{2}{3} &  -\frac{1}{3} & \frac{2}{3}\\
0 & 0 & 0
\end{pmatrix}
\qquad
R=
\begin{pmatrix}
0 & 0 & 0\\
0 & 0 & 0\\
\frac{2}{3} &  \frac{2}{3} & -\frac{1}{3}
\end{pmatrix}
\\
※\vec{\psi} _{0}(0)=
\begin{pmatrix}
\frac{1}{\sqrt{6}}\\
-\frac{2}{\sqrt{6}}\\
\frac{1}{\sqrt{6}} 
\end{pmatrix}
\qquad
\vec{\psi} _{0}(x)=
\begin{pmatrix}
0\\
0\\
0  
\end{pmatrix}
\quad
(x \neq 0)

ちなみにこれ、Glover Walkって名前があります。$P+Q+R$をGlover行列と言います。

2次元格子上の量子ウォーク

さらに、これまで考えてきた1次元量子ウォークを2次元にすることも可能です。
例えば4次の行列で考えると以下のような例があります。

P=
\begin{pmatrix}
\frac{1}{2} & \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{pmatrix}
\qquad
Q=
\begin{pmatrix}
0 & 0 & 0 & 0\\
\frac{1}{2} & \frac{i}{2} & -\frac{1}{2} & -\frac{i}{2}\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0
\end{pmatrix}
\\
R=
\begin{pmatrix}
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
\frac{1}{2} & -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\\
0 & 0 & 0 & 0
\end{pmatrix}
\qquad
S=
\begin{pmatrix}
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
0 & 0 & 0 & 0\\
\frac{1}{2} & -\frac{i}{2} & -\frac{1}{2} & \frac{i}{2}
\end{pmatrix}
\\
※\vec{\psi} _{0}(0,0)=
\begin{pmatrix}
\frac{1}{2}\\
\frac{1}{2}\\
-\frac{1}{2}\\
-\frac{1}{2}
\end{pmatrix}
\qquad
\vec{\psi} _{0}(x,y)=
\begin{pmatrix}
0\\
0\\
0\\
0 
\end{pmatrix}
\quad
(x,y \neq 0)

ちなみにこれは離散Fourier walkという名前がついています。

おわりに

この記事では「はじめてのQuantum Walk」と称して基礎事項の紹介にとどめました。
(本当は発展形も詳しく書きたかったけど、膨大な量になったのでやめました。)

知名度も低く、発展形とその応用に関する研究がまだまだ発展途上にありますが、
この数理モデルこそ現象数理学の発展に今後寄与する可能性があると考えています。

この記事に時間を割いてくださって、ありがとうございました。