多品種輸送問題（あたらしい数理最適化）を実装してみた

• 製造業出身のデータサイエンティストがお送りする記事
• 今回はあたらしい数理最適化の書籍を買ったので、実務で使えそうな部分をアレンジして実装してみました。

##はじめに
業務で最適化を使う機会が増えたので、「あたらしい数理最適化」という書籍を購入したので、実務で使えるように勉強中です。
詳細を載せると問題があるかもしれないので、詳しい内容を知りたい方は書籍を購入してください。

##多品種輸送問題の実装
今回は複数の製品を運ぶための輸送問題を実装しました。使用したライブラリーはmypulpを使いました。書籍ではgurobiが使われているのですが、有料のため無料で使えるmypulpを選定しました。
pythonで数理最適化を実装する際は、pulpが良く使われると思いますが、gurobiと書き方が少し違うので、gurobiと同じような書き方で実装できるmypulpを選定しております。

また実務で使う際は、制約条件とかのデータをcsvで読み込ませて使うことが多いと思いましたので、一部改変しております。

pythonの実装コードは下記です。

# 必要なライブラリーを読み込む
import pandas as pd
from mypulp import *

次に多品種輸送問題を解くためのコードを書いていきます。
下記では、制約条件や目的関数を記載しております。

def mctransp(I, J, K, c, d, M):
    """多品種輸送問題
    
    Arg:
        I(set)  : 顧客番号
        J(list) : 工場番号
        K(list) : 製品番号
        c(dict) : Key:(顧客番号,工場番号,製品番号), Value:輸送費
        d(dict) : Key:(顧客番号,製品番号), Value:需要量
        M(dict) : Key:工場番号, Value:生産容量
        
    Returns:
        a model, ready to be solved.
    """
    # モデルの定義
    model = Model(name = "Multi-product_transportation_problem")

    # 変数を格納する辞書xを作成
    # 変数は輸送費用を表す辞書cのキーが存在する場合にだけ生成
    x = {}
    for i,j,k in c:
        x[i,j,k] = model.addVar(vtype="C")
    model.update()

    arcs = tuplelist([(i,j,k) for (i,j,k) in x])

    # 顧客の需要制約
    for i in I:
        for k in K:
            model.addConstr(quicksum(x[i,j,k] for (i,j,k) in arcs.select(i,"*",k)) == d[i,k])

    # 工場の容量制約
    for j in J:
        model.addConstr(quicksum(x[i,j,k] for (i,j,k) in arcs.select("*",j,"*")) <= M[j])

    # 目的関数
    model.setObjective(quicksum(c[i,j,k]*x[i,j,k]  for (i,j,k) in x), GRB.MINIMIZE)

    model.update()
    model.__data = x
    return model

次は各条件を取得するための関数です。
書籍では、ハードコーディングされていたのですが、csvファイルから読み込む方式へ変更した方が使いやすいと思って少しアレンジしております。

def get_data():
    """インプットデータ取得
    
    Return:
        I(set)  : 顧客番号
        J(list) : 工場番号
        K(list) : 製品番号
        c(dict) : Key:(顧客番号,工場番号,製品番号), Value:輸送費
        d(dict) : Key:(顧客番号,製品番号), Value:需要量
        M(dict) : Key:工場番号, Value:生産容量
    """
    # 工場で製造可能な製品を抽出
    df_p = pd.read_csv('constraints/Multi-product_transportation_problem/produce.csv')
    # DataFrameをdictへ変換
    produce = df_p.set_index('factory').T.to_dict('list') 
    # Nanを削除
    for key in produce.keys():
        produce[key] = {x for x in produce[key] if x==x}
    
    # 顧客と商品の需要量を抽出
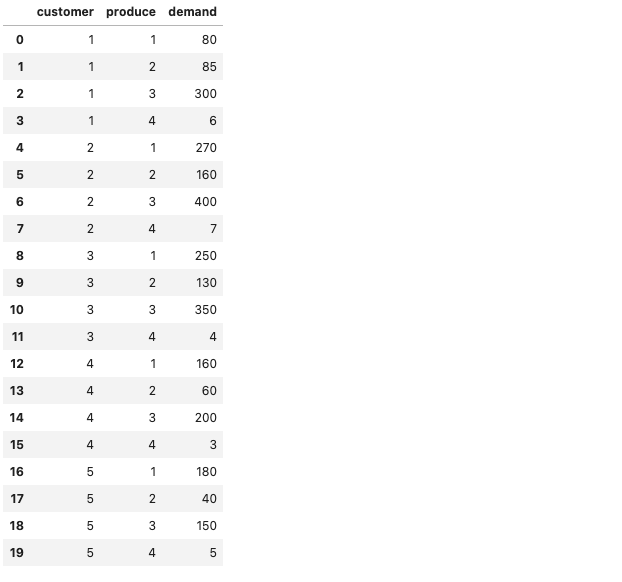
    df_d = pd.read_csv('constraints/Multi-product_transportation_problem/demand.csv')
    # 顧客番号と製品番号のタプル（組）を作成
    D = list(zip(df_d[df_d.columns[0]], df_d[df_d.columns[1]]))
    # 顧客番号と製品番号のタプル（組）をキーとし、需要量を値とする辞書を作成
    d = dict(zip(D, df_d[df_d.columns[2]]))
    
    # 顧客番号Iを生成
    I = set([i for (i,k) in d])
    # 工場の番号リストJと生産容量Mをmultidictを用いて作成
    J, M = multidict({1:3000, 2:3000, 3:3000})
    # 製品番号リストKと重量weightをmultidictを用いて作成
    K, weight = multidict({1:5, 2:2, 3:3, 4:4})
    
    # 顧客と商品の輸送費用を抽出
    df_c = pd.read_csv('constraints/Multi-product_transportation_problem/cost.csv')
    # 顧客番号と製品番号のタプル（組）を作成
    C = list(zip(df_c[df_c.columns[0]], df_c[df_c.columns[1]]))
    # 顧客番号と製品番号のタプル（組）をキーとし、輸送費用を値とする辞書を作成
    cost = dict(zip(C, df_c[df_c.columns[2]]))
    
    # weightとcostから製品毎の輸送費用を計算し、辞書cに保管
    c = {}
    for i in I:
        for j in J:
            for k in produce[j]:
                c[i, j, k] = cost[i, j] * weight[k]

    return I, J, K, c, d, M

最後に最適化を解きます。

if __name__ == "__main__":
    I, J, K, c, d, M = get_data()
    model = mctransp(I, J, K, c, d, M)
    # 最適化の実行
    model.optimize()
    print("Opt value:", model.ObjVal)

# Opt value: 43536.0

ご参考までに使用したcsvファイルを記載します。

# 工場で製造可能な製品を抽出
    df_p = pd.read_csv('constraints/Multi-product_transportation_problem/produce.csv')
    # DataFrameをdictへ変換
    produce = df_p.set_index('factory').T.to_dict('list') 
    # Nanを削除
    for key in produce.keys():
        produce[key] = {x for x in produce[key] if x==x}

# produce
# {1: {2.0, 4.0}, 2: {1.0, 2.0, 3.0}, 3: {2.0, 3.0, 4.0}}

# 顧客と商品の需要量を抽出
df_d = pd.read_csv('constraints/Multi-product_transportation_problem/demand.csv')
# 顧客番号と製品番号のタプル（組）を作成
D = list(zip(df_d[df_d.columns[0]], df_d[df_d.columns[1]]))
# 顧客番号と製品番号のタプル（組）をキーとし、需要量を値とする辞書を作成
d = dict(zip(D, df_d[df_d.columns[2]]))

# d
# d = {(1,1):80,   (1,2):85,   (1,3):300, (1,4):6,
#      (2,1):270,  (2,2):160,  (2,3):400, (2,4):7,
#      (3,1):250,  (3,2):130,  (3,3):350, (3,4):4,
#      (4,1):160,  (4,2):60,   (4,3):200, (4,4):3,
#      (5,1):180,  (5,2):40,   (5,3):150, (5,4):5
#     }

# 顧客と商品の輸送費用を抽出
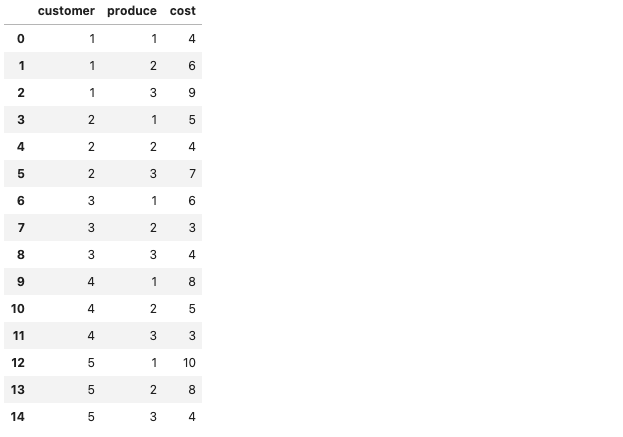
df_c = pd.read_csv('constraints/Multi-product_transportation_problem/cost.csv')
# 顧客番号と製品番号のタプル（組）を作成
C = list(zip(df_c[df_c.columns[0]], df_c[df_c.columns[1]]))
# 顧客番号と製品番号のタプル（組）をキーとし、輸送費用を値とする辞書を作成
cost = dict(zip(C, df_c[df_c.columns[2]]))

# cost
# cost = {(1,1):4,  (1,2):6,  (1,3):9,
#         (2,1):5,  (2,2):4,  (2,3):7,
#         (3,1):6,  (3,2):3,  (3,3):4,
#         (4,1):8,  (4,2):5,  (4,3):3,
#         (5,1):10, (5,2):8,  (5,3):4,
#        }

##さいごに
最後まで読んで頂き、ありがとうございました。
製造現場において最適化が求められることは多いので、引き続き数理最適化を勉強していこうと思います。

訂正要望がありましたら、ご連絡頂けますと幸いです。