- 製造業出身のデータサイエンティストがお送りする記事
- 今回は多目的最適化手法の中で、NSGA-Ⅲを勉強しましたので、整理しました。
はじめに
NSGA-Ⅲは前回ご紹介したNSGA-Ⅱを改良したモデルになりますので、NSGA-Ⅱと合わせて見て頂くと良いかと思います。
NSGA-Ⅲとは
NSGA-Ⅲの特徴は下記2点があります。
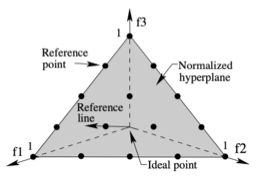
- Reference point(参照点)の導入
- Reference lineを活用した個体選択
NSGA-Ⅲのアルゴリズム概要
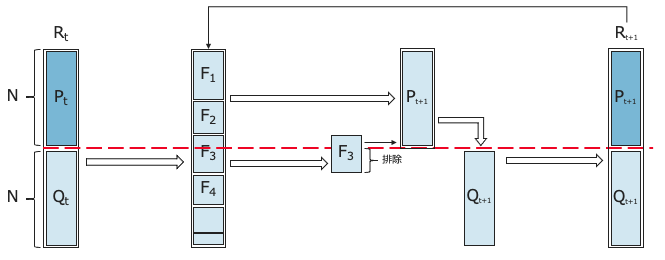
NSGA-Ⅲでは、親母集団$P_t$と遺伝子操作(交叉・突然変異)を行って探索を行うための子母集団$Q_t$の2つの独立した集団を用いて解探索を行う手法です(NSGA-Ⅱと同じ)。具体的なアルゴリズムの流れは下記の通りです。
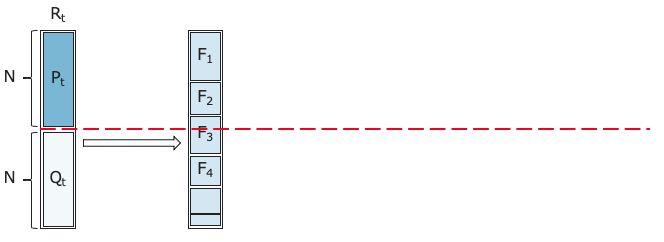
① サイズNの親母集団$P_t$をランダムに生成し、サイズNの子母集団$Q_t$を生成し、$P_t$と$Q_t$を組合せて集団$R_t$を生成する。
② 集団$R_t$に対して非優劣ソートを実施し、全個体をランク毎($F_1$, $F_2$, ・・・)と分類する。
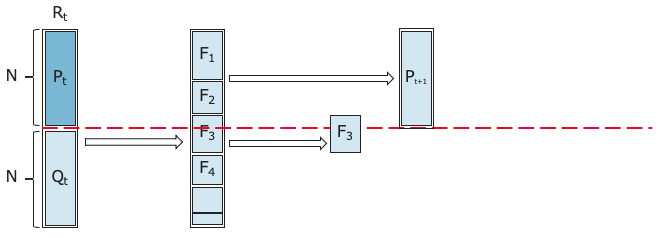
③ 新たな空の親母集団$P_{t+1}$を生成し、②の非優劣ソートでランクが上位の個体で親母集団$P_{t+1}$を構成していく。
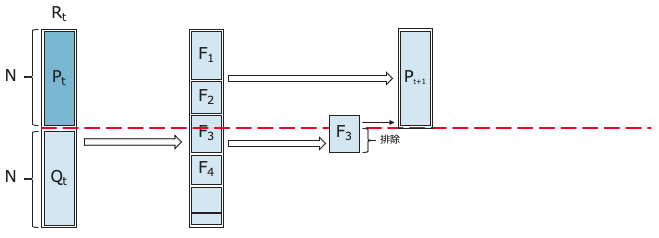
④ **[変更点]**③で親母集団$P_{t+1}$を構成していく途中で、個体サイズがNを越える時、サイズNを越えるランクの個体に対して、Reference lineを参照して個体を選択する。
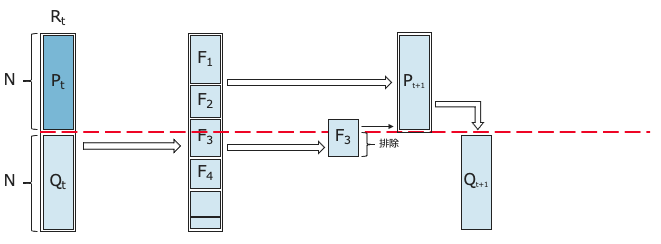
⑤ [変更点]親母集団$P_{t+1}$に対してReference lineを活用して適合度評価により、交叉・突然変異すべき個体を選択し、遺伝子操作を行い新たな子集団$Q_{t+1}$を生成する。
⑥ 親母集団$P_{t+1}$と子集団$Q_{t+1}$を組み合わせて新たな集団$R_{t+1}$を生成する。
⑦ ②へ戻り、これまでの操作を終了条件が満たすまで繰り返し実施します。
Reference lineを活用した適合度の計算方法とは
下記手順によって計算されております。
① 各個体と各reference lineとのベクトルの直交距離を計算し、各個体の最近傍のreference lineを決定する。
② 近傍個体数の最も少ないreference lineを選び、対象ランクの個体集合でそのreference lineに最も直交距離の近い個体を次世代個体として選択する
NSGA-ⅡとNSGA-Ⅲの比較表
| 手法 | 特徴 |
|---|---|
| NSGA-Ⅱ | ・目的変数の数が少ないと良好な結果が得られる ・目的変数が多く高次元になると混雑距離で解の優劣が付けにくくなり、収束性が悪くなる |
| NSGA-Ⅲ | ・reference lineで解の探索方向を予め定めておくことで、目的変数が多く高次元になっても高い収束性を実現できる。 |
さいごに
最後まで読んで頂き、ありがとうございました。
今回は多目的最適化問題のNSGA-Ⅲを整理しました。理論的な違いは概ね理解できたのですが、実際の業務に当てはまる際にどちらが良いのかは両方試してみる必要があるかなと思いました。
次は実装したものを纏めたいと思います。
訂正要望がありましたら、ご連絡頂けますと幸いです。