- 製造業出身のデータサイエンティストがお送りする記事
- 今回は隠れマルコフモデルを用いた異常検知を実装してみました。
はじめに
今回は、汎用性の高い時系列分析モデルの隠れマルコフモデルを用いた異常検知手法を実装してみました。
隠れマルコフモデルを用いた異常検知とは
今回は理論的な部分の詳細は割愛しますが、データの背後にある「状態」の系列を導入しう、モデルを構築するデータの発生確率を予測し、異常検知を行っていきます。下記に簡単に特徴を記載しておきます。
- 汎用性の高い時系列モデルである
- 観測できない隠れた状態を仮定しており、状態はそれぞれ異なる出力の確率分布を持ちます
- 状態の遷移確率や状態毎に得られる発生確率を計算することで複雑な時系列データの異常を検知できます。
今回使用するデータセットは下記です。
- qtdb/sel102 ECG datasetという、心電図データを用います。
- URL:http://www.cs.ucr.edu/~eamonn/discords/
pythonのコードは下記の通りです。
# 必要なライブラリーのインポート
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# 必要な関数を読み込む
from hmmlearn import hmm
df = np.loadtxt("qtdbsel102.txt", delimiter="\t")
# 3列目のデータを使用
# trainデータ, testデータを作成
train_df = df[0:3000, 2]
test_df = df[3000:6000, 2]
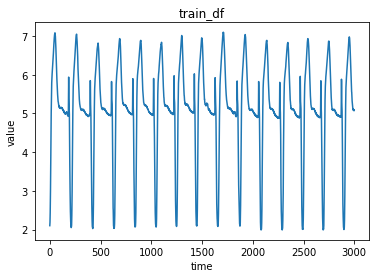
# 学習データの可視化
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.grid(False)
ax.plot(train_df)
ax.set_title('train_df')
ax.set_ylabel('value')
ax.set_xlabel('time')
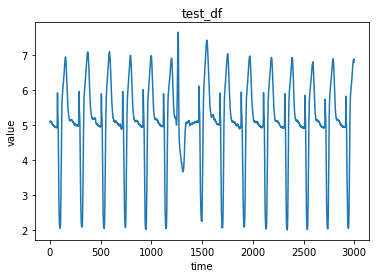
# 評価データの可視化
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.grid(False)
ax.plot(test_df)
ax.set_title('test_df')
ax.set_ylabel('value')
ax.set_xlabel('time')
学習データと評価データの特徴が分かったところで、次に分布の推定を行っていきます。
num_states = 15
X = train_df.reshape(-1, 1)
lengths = [len(train_df)]
np.random.seed(seed=7)
model = hmm.GaussianHMM(n_components=num_states, covariance_type='full')
model.fit(X, lengths)
今回は状態の種類数(num_states)は15としました。
hmmlearnライブラリーを使用する際は、hmmlearn.GaussianHMM.fit()を使用します。
次に分布の推定で算出したパラメータを用いて異常度を算出します。
# model.scores()関数では、系列x'の対数尤度p(log(x'))が計算される。
logprob = np.array([model.score(train_df[0:i+1].reshape(-1, 1)) for i in range(len(train_df))])
train_abnormality = -np.append(logprob[0], np.diff(logprob))
# 閾値の設定
ratio = 0.005 # 異常と判断する割合
threshold = np.sort(train_abnormality)[int((1-ratio)*len(train_abnormality))]
print(threshold)
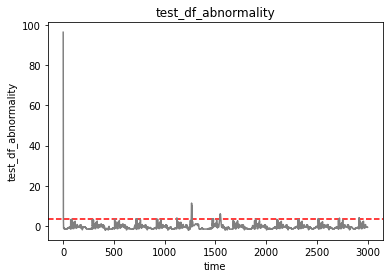
最後に構築したモデルを活用して異常検知を行う。
# 評価データの異常検知
logprob = np.array([model.score(test_df[0:i+1].reshape(-1, 1)) for i in range(len(test_df))])
test_abnormality = -np.append(logprob[0], np.diff(logprob))
# 評価データの異常度を可視化
# 管理限界を破線で示す
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.grid(False)
ax.axhline(threshold, ls="--", color="red")
ax.plot(test_abnormality, color="gray")
ax.set_title('test_df_abnormality')
ax.set_xlabel('time')
ax.set_ylabel('test_df_abnormality')
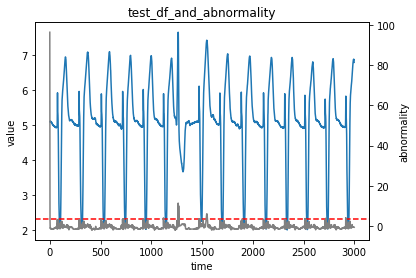
最後に評価データと異常度を一緒に可視化してみようと思います。
# 評価データの異常度を可視化
# 管理限界を破線で示す
fig = plt.figure()
ax1 = fig.add_subplot(1,1,1)
ax1.grid(False)
# ax1とax2を関連させる
ax2 = ax1.twinx()
ax2.axhline(threshold, ls="--", color="red")
ax1.plot(test_df)
ax2.plot(test_abnormality, color="gray")
ax1.set_title('test_df_and_abnormality')
ax1.set_ylabel('value')
ax1.set_xlabel('time')
ax2.set_ylabel('abnormality')
比較的簡単に実装できました。ただ、計算コストが少し高いため、実務で使う際は計算時間も考慮する必要がありそうです。
また、状態数が多いほど複雑な構造になりますが、明確な決定根拠が無いため、現場のデータに合わせた適切な状態数を決定する必要がありそうです。
さいごに
最後まで読んで頂き、ありがとうございました。
今回は隠れマルコフモデルを用いた異常検知を実装してみました。
訂正要望がありましたら、ご連絡頂けますと幸いです。