グラフをコミュニティに（重なりなく）分割する手法の1つであるスピングラス法について説明します（詳細な説明まで書き切れていないので説明の入口程度と思ってください）。グラフやコミュニティの説明などは以下に記しますが、先にまとめるとスピングラス法とは、

「エッジでつながったノードどうしは同じコミュニティ／エッジでつながっていないノードどうしは異なるコミュニティになるように、個々のノードが所属するコミュニティを割り当てる」というグラフのコミュニティ分割問題を、
「スピングラス中の正の相互作用をするスピンどうしは同じ状態／負の相互作用をするスピンどうしは異なる状態になるように、個々のスピンの状態を割り当てる」という統計力学の問題に読み換えて、
スピングラスの基底状態をシミュレーティドアニーリングで最適化する。

ことによってコミュニティ分割する手法といえます。ここで、

スピングラス法は「それまでのコミュニティ分割手法とは全く異なる手法」というよりは、「それまでのコミュニティ分割手法（のいくつか）の目的関数を統一的に記述しさらに適用範囲を広げたもの」であり、それまでの手法のいくつかを特殊な場合として含んでいます。
「スピングラス法」という表現自体は「コミュニティ分割の目的関数をスピングラスのハミルトニアンと同一視する」ことまでしか指していないと（私は）思うのですが、文脈によっては「その目的関数をシミュレーティドアニーリングで最適化する」まで含んでいるようです。
- 参考文献1. のスピングラス法の原論文ではシミュレーティドアニーリングが効果的な解法として紹介されていますので、この論文全体が示す一連の手順がスピングラス法と解釈するなら、「シミュレーティドアニーリングで最適化する」までが「スピングラス法」といえそうです。
- スピングラス法の名が付いている igraph パッケージの cluster_spinglass 関数で最適化にシミュレーティドアニーリングが用いられているためか、コミュニティ検出の文脈で「スピングラス法」と「シミュレーティドアニーリング」が混同されている場合があるようです。しかし、スピングラス方式の目的関数をシミュレーティドアニーリングではない方法で解くこともやろうと思えばできますし、スピングラス方式ではない目的関数をシミュレーティドアニーリングで解くこともできます。igraph のドキュメントには ”This function tries to find communities in graphs via a spin-glass model and simulated annealing.” とあり、「スピングラスモデルとシミュレーティドアニーリングの組合せ」であることが明記されています。
何にせよ、以下の2点は分けて理解したいです。
- 「コミュニティ分割の目的関数をスピングラスのハミルトニアンと同一視する」ことの価値は、コミュニティ検出を統計物理学の観点から定式化することで種々の検出手法を統一的に記述し、適用範囲を拡張し、さらにコミュニティ構造がオーバーラップしているか／階層的であるかの評価も可能にし、モジュラリティの期待値を求めることもできるようにしたこと。
- 「シミュレーティドアニーリングで解く」ことの価値は、複雑な目的関数に対して品質のよい解が求まること。

参考文献

J. Reichardt and S. Bornholdt: Statistical Mechanics of Community Detection, Phys. Rev. E, 74, 016110 (2006) ― グラフをコミュニティに分割する問題が、無限長距離の相互作用をもつスピングラスの基底状態を求める問題と同一視できることを示した論文です。下の igraph パッケージの cluster_spinglass 関数のオリジナルコードを書いたのがこの著者の方です。
- https://arxiv.org/abs/cond-mat/0603718
igraph ― スピングラス法が含まれているグラフ解析用パッケージです。R, Python, C/C++ で利用できます。
- http://igraph.org/
- http://igraph.org/r/ （R向けのパッケージのページ）
- http://igraph.org/r/doc/igraph.pdf （R向けのパッケージのドキュメント）

グラフって何

ここでグラフといっているのは数値データを折れ線や棒に視覚化する方のグラフではなく、ノードの集合及びどのノード間がエッジで結ばれているかを定義したデータ構造のことです（こちらの意味のグラフの性質を調べる学問がグラフ理論です）。例えば、静岡県のすべての市区町村をノードと見做し、隣接する市区町村の間には方向のないエッジがあると定義すれば、これはグラフになります。特に、エッジに向きがなく、結び付きが強いエッジと弱いエッジの区別もないので、「重みなし無向グラフ」になります。

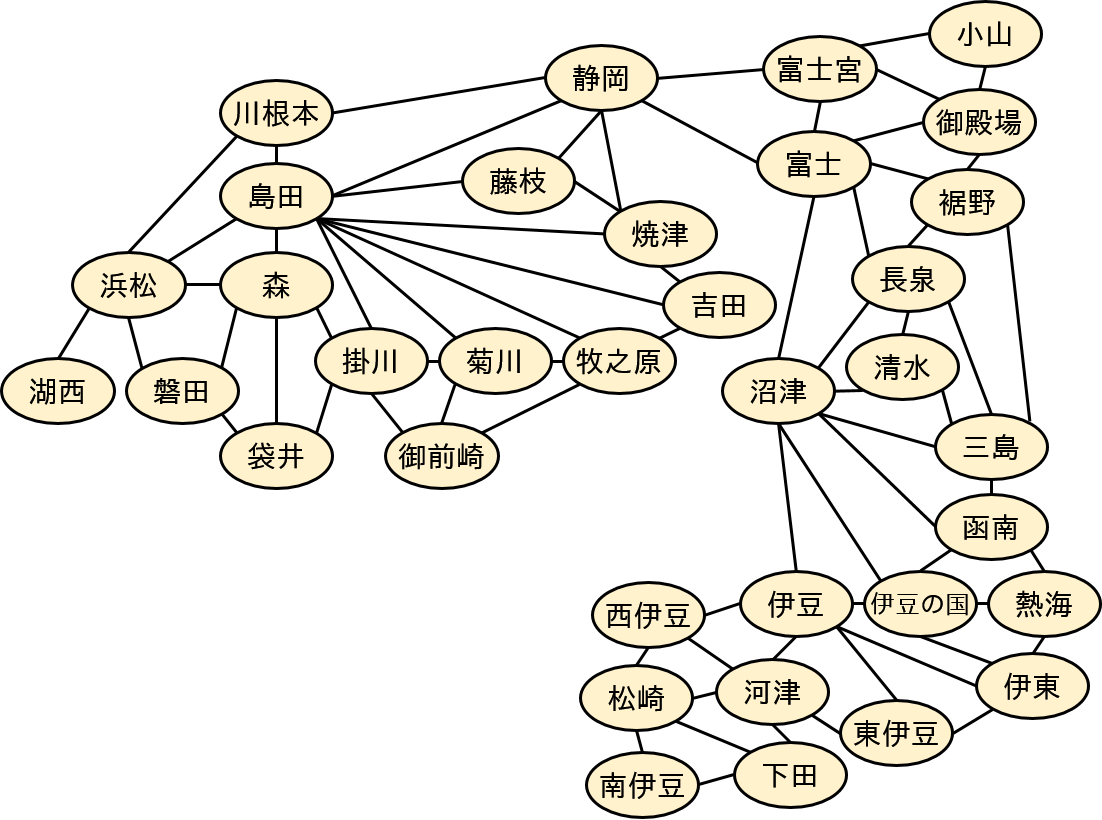
ちなみに、上の構造を適切に R igraph に取り入れて描画すると以下のようになります。伊豆半島が北西にきてしまいましたがあまり気にしないことにします（描画時のノード配置は乱数に依存します；繰り返し同じ配置で描画したいときは set.seed() で乱数の種を固定します）。

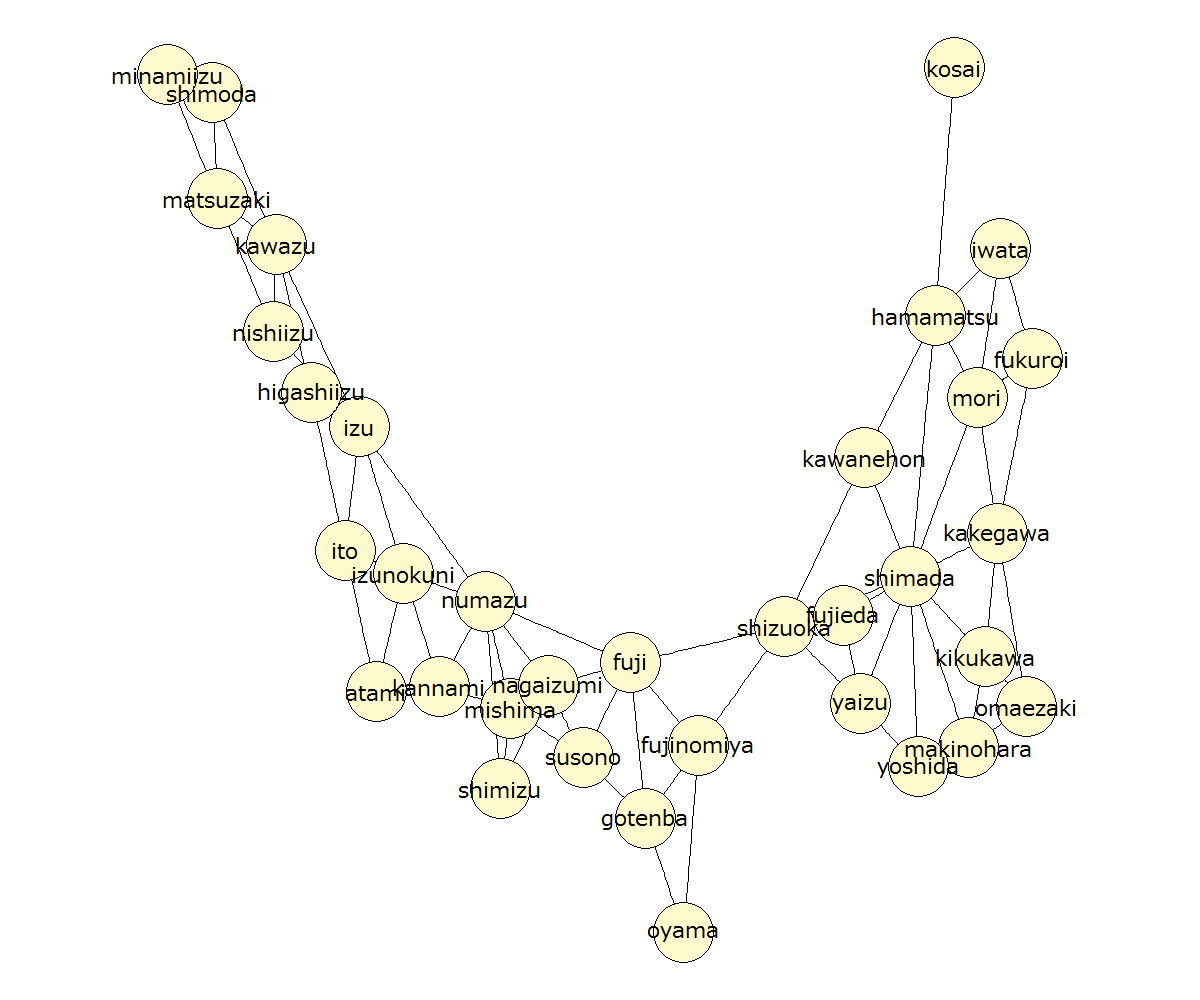
コミュニティって何

グラフ理論でいう「コミュニティ」には文献によって定義が異なることもあり、数学的に厳密な共通の定義はありません。ただし、大まかな意味合いは共通していて、なるべく以下の2つの要件を満たすようにグラフをいくつかに分けた各部分部分をコミュニティといいます。

同じコミュニティに所属するノードどうしは、結び付きが密になるようにする。
違うコミュニティに所属するノードどうしは、結び付きが疎になるようにする。

この要件はとても曖昧で、具体的に何をもって結び付きの疎密とするかとか、この2つの要件のどちらをより重んじるべきかとかを決めなければコミュニティ分割はできませんが、そのような具体的な要件は個々のコミュニティ分割手法が定めています。つまり、スピングラス法のような種々のコミュニティ分割手法は、「厳密に何をもって『よいコミュニティ分割』とするか」の定義から含めて「『よいコミュニティ分割』を具体的にどのように求めるか」を示すものといえるでしょう。

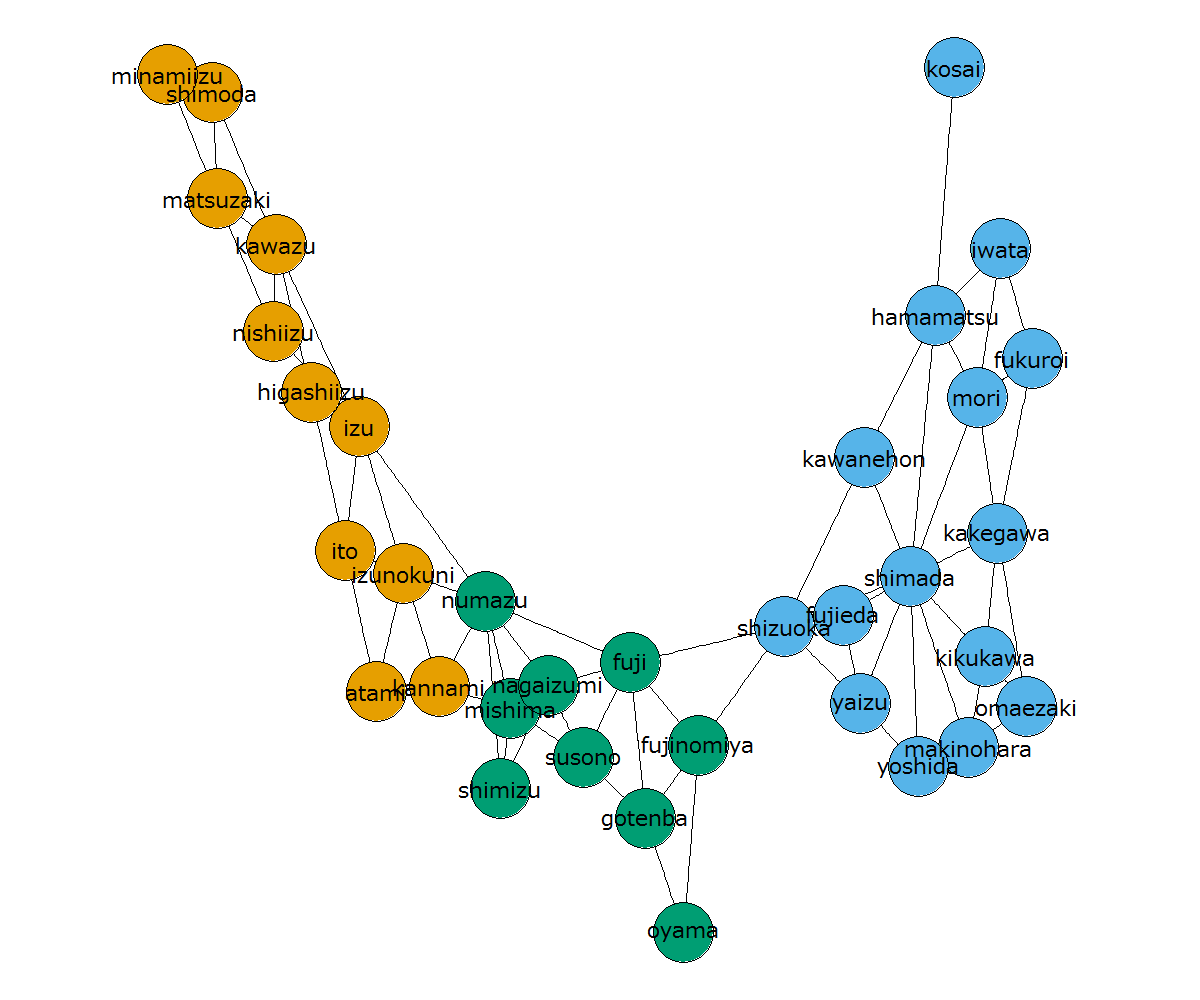
コミュニティ分割の実例を示します。先の静岡県を igraph のスピングラス法（パラメータはデフォルト値）でコミュニティ分割すると以下のように分割されます（ただし、乱数に依存します）。

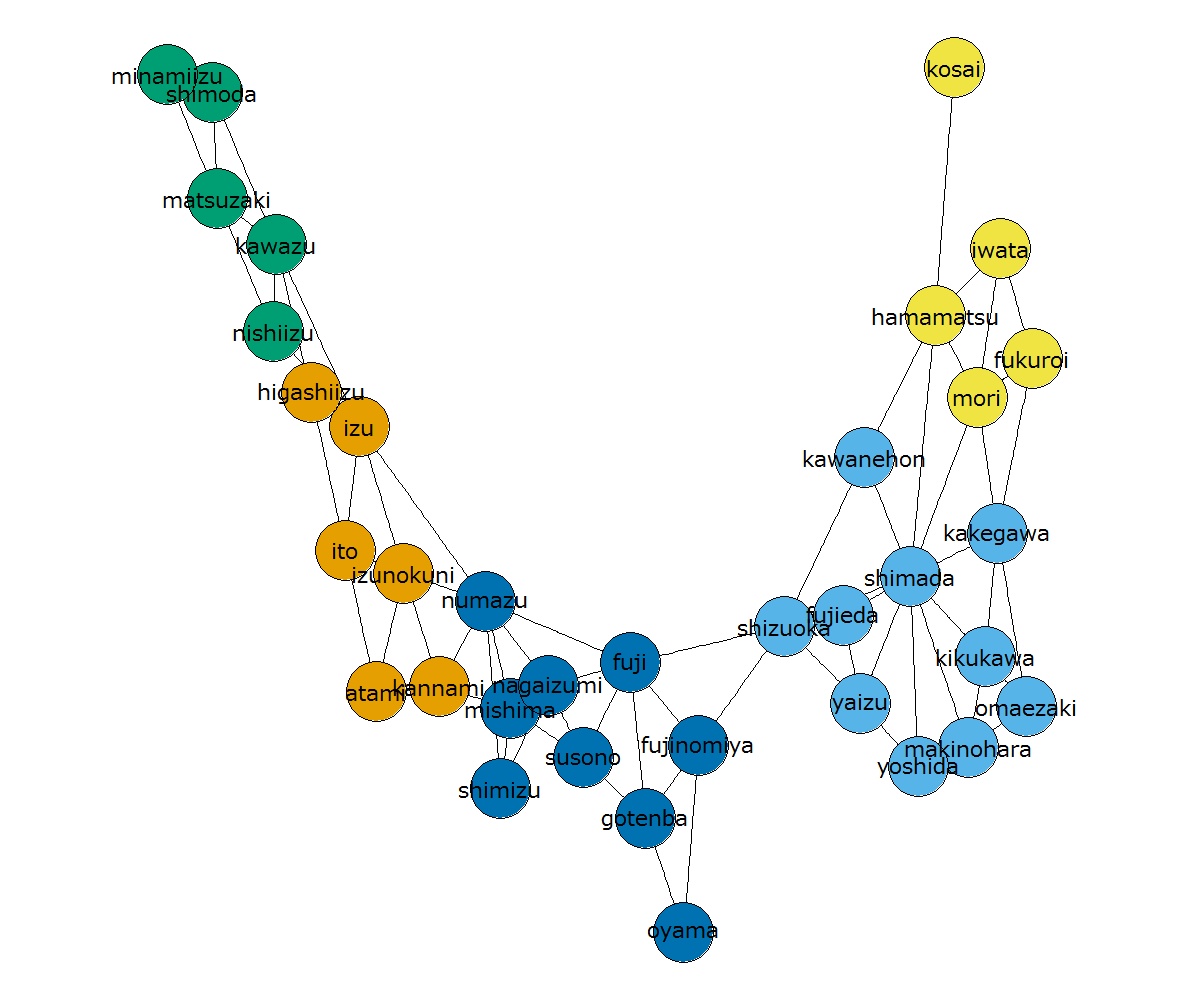
上図は5つのコミュニティに分割されていますが、「静岡市は隣接する富士市や焼津市とは同じコミュニティに所属してほしい」「静岡市は隣接しない浜松市や伊豆市とは違うコミュニティに所属してほしい」というのを色々考慮した結果、このようになっています。「静岡市と富士市は隣接するのに異なるコミュニティになってしまうのか」と思われるかもしれませんが、ここで富士市を静岡市側のコミュニティに入れてしまうと、「隣接しているのに違う色の市町村」「隣接していないのに同じ色の市町村」がかえって増えてしまい、コミュニティに求められる2つの要件の達成度が低くなってしまいます。

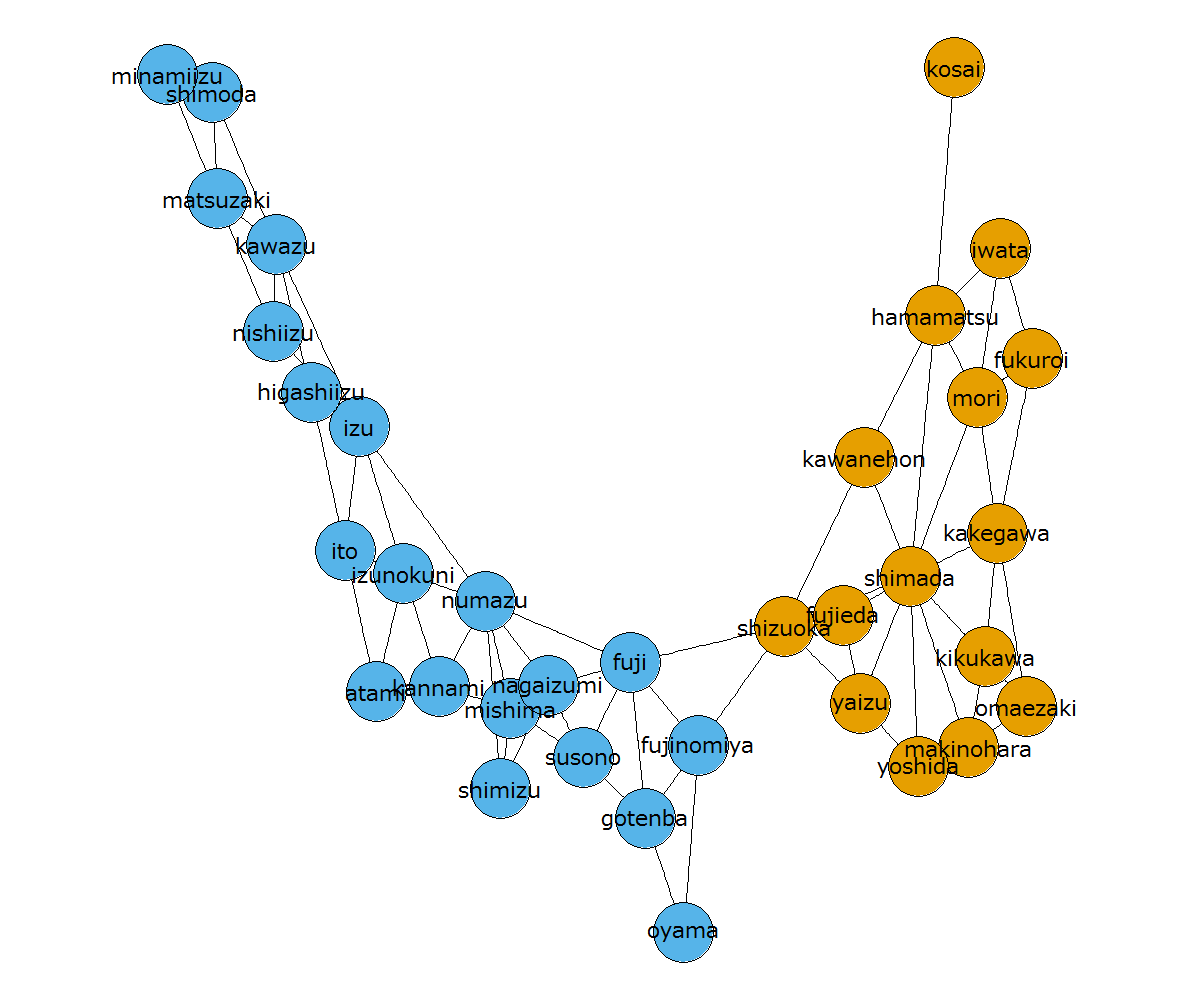
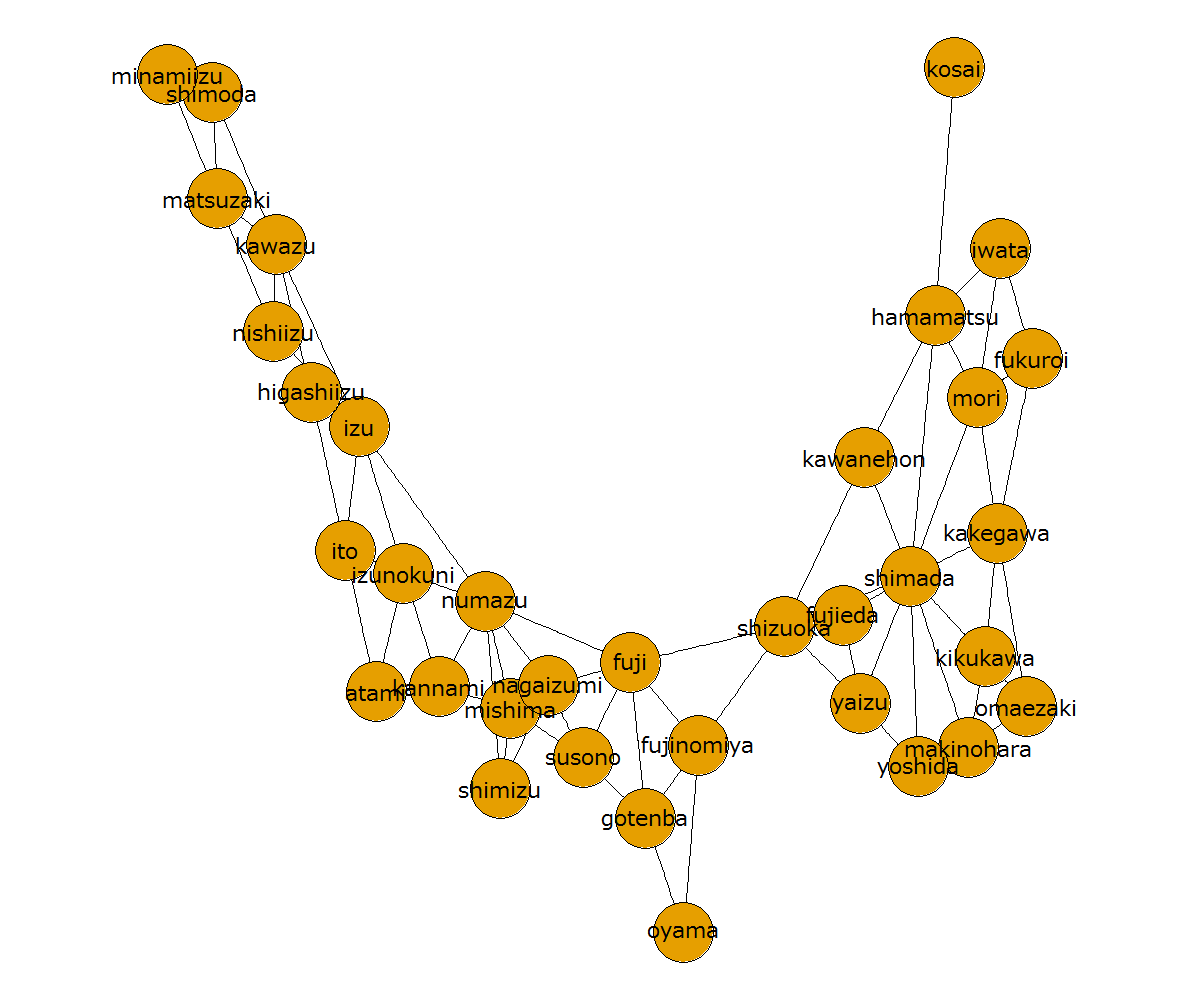
なお、同じコミュニティ分割手法でも設定するパラメータによって分割結果は異なります。スピングラス法にもいくつかのパラメータがありますが、例えば gamma というパラメータは「『エッジでつながっていないこと』を、『エッジでつながっていること』の何倍重んじるか」という意味合いのパラメータになります。デフォルト値は1です。この gamma を 1.5、0.5、0.01、0 と変更してコミュニティ分割をすると下図のようになります。gamma が小さくなるほど静岡県が統一されていきます。

上図の結果について大まかに説明します。スピングラス法における目的関数には以下の1～4の4つの項がありますが、例えば gamma を 0 にしていくと（「エッジでつながっていないこと」を全く考慮しないので） 2. と 4. の項を無視していくことになります。2. と 4. を無視して 1. と 3. だけ考慮すると、「すべてのノードを同じコミュニティにする」が最適な答えになるのがわかると思います（ので、gamma を 0 にするべきではないでしょう）。

同じコミュニティに所属するノードどうしがつながっていたら報酬
同じコミュニティに所属するノードどうしがつながっていなかったらペナルティ
違うコミュニティに所属するノードどうしがつながっていたらペナルティ
違うコミュニティに所属するノードどうしがつながっていなかったら報酬

スピングラス法って何

上の 1～4 のセットは、「同じコミュニティは結び付きが密になるようにする」「異なるコミュニティは結び付きが疎になるようにする」というコミュニティ分割を達成したいときに目的関数に含めるべき項として1つ自然な考え方になっていると思います。これを数式に表すと、任意に割り振ったコミュニティがどれだけよいものかは、各ノードの所属コミュニティを $ \sigma_1, \sigma_2, \cdots $ とすると、以下の関数が小さければ小さいほどよい、ということになります。

\mathcal{H}(\{\sigma\}) = - \sum_{i \neq j} a_{ij} A_{ij} \delta (\sigma_i, \sigma_j) + \sum_{i \neq j} b_{ij} (1 - A_{ij}) \delta (\sigma_i, \sigma_j) - \sum_{i \neq j} c_{ij} A_{ij} \Bigl( 1 - \delta (\sigma_i, \sigma_j) \Bigr) + \sum_{i \neq j} d_{ij} (1 - A_{ij}) \Bigl( 1 - \delta (\sigma_i, \sigma_j) \Bigr)

ここで、$A_{ij}$ はノード $i$ と $j$ の間にエッジがあるかどうか（重みなしグラフなら0か1；重み付きグラフなら0か1以下の正数）、$\delta (\sigma_i, \sigma_j)$ はノード $i$ と $j$ の所属コミュニティ $\sigma_i$ と $\sigma_j$ が一致しているかどうか（0か1）です。$a_{ij}, b_{ij}, c_{ij}, d_{ij}$ はそれぞれ以下のような意味合いになります。特に重みを付けなくてもよいという場合は全て1としても構いません。

$a_{ij}$ ：ノード $i$ と $j$ が同じコミュニティに所属しかつエッジでつながっている場合の報酬に、どれだけ重みを付けるか。
$b_{ij}$ ：ノード $i$ と $j$ が同じコミュニティに所属しかつエッジでつながっていない場合のペナルティに、どれだけ重みを付けるか。
$c_{ij}$ ：ノード $i$ と $j$ が異なるコミュニティに所属しかつエッジでつながっている場合のペナルティに、どれだけ重みを付けるか。
$d_{ij}$ ：ノード $i$ と $j$ が異なるコミュニティに所属しかつエッジでつながっていない場合の報酬に、どれだけ重みを付けるか。

静岡県をスピングラス法でコミュニティ分割した例の（全部は面倒なので）6つの市だけ切り取って $\mathcal{H}$ を計算してみると $-18$ になります（$a_{ij}=b_{ij}=c_{ij}=d_{ij}=1$ の場合）。コミュニティの色分けを変えて静岡市を別のコミュニティに切り離すと $\mathcal{H}=-6$ 、6市をすべて同じコミュニティにすると $\mathcal{H}=-2$ となることも確かめられます。なので、下図の色分けはこれらの別の色分けよりもよい（$\mathcal{H}$ がより小さい）ということがわかると思います。

上で定義した $\mathcal{H}$ は、スピングラスという物質において各スピンが状態 $ \sigma_1, \sigma_2, \cdots $ をとったときのエネルギーと読み換えることができます。

スピングラスとは、スピンというものが乱雑な配置に（結晶のように規則正しくなく）固まったものです。
- 乱雑な配置であるために任意の2つのスピンどうしは乱雑な相互作用をもちます。
- 正の相互作用をするスピンは同じ状態を取る方がエネルギーが小さくなり、負の相互作用をするスピンどうしは異なる状態を取る方がエネルギーが小さくなります。
- 静岡県のコミュニティ分割で隣接する静岡市と富士市が異なるコミュニティになってしまったように、スピングラスにおいても全体のエネルギーを最小化するには正の相互作用をもつスピンどうしに異なる状態を割り当てなければならないことがあります（このようにすべての相互作用に対してエネルギーを最小化する状態を取れないことを物理の用語でフラストレーションといいます）。
特にこの場合は、1～4 の報酬やペナルティは近いノードのペアだけでなく全てのノードのペアに対して考えられるので、無限長距離の相互作用をもつスピングラスを考えていることになります。

この $\mathcal{H}$ を最適化するようなコミュニティの割り当て（スピン状態の割り当て）$ \sigma_1, \sigma_2, \cdots $ を求めなければなりませんが、今回参照している論文では、シミュレーティドアニーリングという手法による求め方が紹介されています。シミュレーティドアニーリングを採用する理由は、質のよい解が求まり、シミュレーティドアニーリングのスピングラス問題への適用もポピュラーであり、実装もシンプルであるからとされています。

シミュレーティドアニーリングとは、目的の関数の最小値を数値計算的に求める手法の1つです。特に変数が多い（探索空間が広い）ときに有効なことが知られています。
- スピングラスにおいてはスピンの数だけ変数があり、探索すべきスピンの状態のパターン数は膨大になります（ $N$ 個のスピンが $2$ 種類の状態を取るならば、パターン数は $2^N$ ）。
シミュレーティドアニーリングは鋼の焼きなまし（アニーリング）にヒントを得た手法です。金属工学において焼きなましとは、鋼をゆっくりと冷やすことにより、内部にひずみのない、加工しやすい状態にする処理を指します。シミュレーティドアニーリングではこの過程をコンピュータ的に再現し、目的関数を鋼のエネルギー、探索空間を鋼の状態とみなし、ゆっくりと温度を下げながら鋼のエネルギー最小の（最もひずみがない）状態に固めることを目指します。
- たくさんの変数のうち一部の変数を変更しながら解を更新していきますが、温度が高いうちはエネルギーが小さくなる方向に遷移する確率が低めで、色々な状態を探索します。温度が低くなってきたら、エネルギーが小さくなる方向を目指す確率が高くなっていきます。
  - 最初からエネルギーが小さくなる方向ばかり目指すと局所解にしかたどり着けません。

（おまけ）Rでグラフを図示するスクリプト

静岡県のグラフ構造を図示する誰得スクリプトです。

test.R

# 静岡県の市区町村の一覧
names <- c("shizuoka", "hamamatsu", "numazu", "atami", "mishima",
           "fujinomiya", "ito", "shimada", "fuji", "iwata",
           "yaizu", "kakegawa", "fujieda", "gotenba", "fukuroi",
           "shimoda", "susono", "kosai", "izu", "omaezaki",
           "kikukawa", "izunokuni", "makinohara", "higashiizu", "kawazu",
           "minamiizu", "matsuzaki", "nishiizu", "kannami", "shimizu",
           "nagaizumi", "oyama", "yoshida", "kawanehon", "mori")

# 隣接市区町村の一覧
get_neighbors <- function(name) {
  return(switch(name,
    "shizuoka"=c("fujinomiya", "fuji", "yaizu", "fujieda", "shimada", "kawanehon"),
    "hamamatsu"=c("kosai", "iwata", "mori", "shimada", "kawanehon"),
    "numazu"=c("fuji", "nagaizumi", "shimizu", "mishima", "kannami", "izunokuni",
               "izu"),
    "atami"=c("ito", "izunokuni", "kannami"),
    "mishima"=c("kannami", "numazu", "shimizu", "nagaizumi", "susono"),
    "fujinomiya"=c("oyama", "gotenba", "fuji", "shizuoka"),
    "ito"=c("higashiizu", "izu", "izunokuni", "atami"),
    "shimada"=c("mori", "hamamatsu", "kawanehon", "shizuoka", "fujieda", "yaizu",
                "yoshida", "makinohara", "kikukawa", "kakegawa"),
    "fuji"=c("gotenba", "susono", "nagaizumi", "numazu", "shizuoka", "fujinomiya"),
    "iwata"=c("hamamatsu", "mori", "fukuroi"),
    "yaizu"=c("yoshida", "shimada", "fujieda", "shizuoka"),
    "kakegawa"=c("omaezaki", "fukuroi", "mori", "shimada", "kikukawa"),
    "fujieda"=c("yaizu", "shimada", "shizuoka"),
    "gotenba"=c("susono", "fuji", "fujinomiya", "oyama"),
    "fukuroi"=c("iwata", "mori", "kakegawa"),
    "shimoda"=c("minamiizu", "matsuzaki", "kawazu"),
    "susono"=c("mishima", "nagaizumi", "fuji", "gotenba"),
    "kosai"=c("hamamatsu"),
    "izu"=c("numazu", "izunokuni", "ito", "higashiizu", "kawazu", "nishiizu"),
    "omaezaki"=c("makinohara", "kikukawa", "kakegawa"),
    "kikukawa"=c("omaezaki", "kakegawa", "shimada", "makinohara"),
    "izunokuni"=c("ito", "izu", "numazu", "kannami", "atami"),
    "makinohara"=c("omaezaki", "kikukawa", "shimada", "yoshida"),
    "higashiizu"=c("kawazu", "izu", "ito"),
    "kawazu"=c("shimoda", "matsuzaki", "nishiizu", "izu", "higashiizu"),
    "minamiizu"=c("shimoda", "matsuzaki"),
    "matsuzaki"=c("minamiizu", "shimoda", "kawazu", "nishiizu"),
    "nishiizu"=c("izu", "kawazu", "matsuzaki"),
    "kannami"=c("mishima", "numazu", "izunokuni", "atami"),
    "shimizu"=c("nagaizumi", "numazu", "mishima"),
    "nagaizumi"=c("susono", "fuji", "numazu", "shimizu", "mishima"),
    "oyama"=c("fujinomiya", "gotenba"),
    "yoshida"=c("makinohara", "shimada", "yaizu"),
    "kawanehon"=c("hamamatsu", "shimada", "shizuoka"),
    "mori"=c("kakegawa", "fukuroi", "iwata", "hamamatsu", "shimada"),
    c()))
}

# ----------------------------------------------------------------------
library(igraph)
windowsFonts(MEI=windowsFont("Meiryo"))

# エッジリストの作成
V0 <-c() # エッジの始点
V1 <-c() # エッジの終点
for (name in names) {
  id <- which(names==name)
  neighbors <- get_neighbors(name)
  neighbors_id <- sapply(neighbors, function(x){return(which(names==x))})
  neighbors <- neighbors[neighbors_id > id]
  if (length(neighbors) > 0) {
    V0 <- c(V0, rep(name, length(neighbors)))
    V1 <- c(V1, neighbors)
  }
}
my_graph <- data.frame(V0=V0, V1=V1)

# ネットワークの作成
g <- graph.data.frame(my_graph, directed=F) # ネットワーク

# ネットワークの図示
png("test.png", pointsize=18, width=1200, height=1000)
par(mar=c(0,0,0,0))
set.seed(12345)
plot(g,
  vertex.size=14,
  vertex.label.color="black",
  vertex.color="lemonchiffon",
  vertex.label.cex=1.2,
  vertex.label.family="MEI",
  edge.color="black")
dev.off()

# コミュニティ分割と図示
communities <- cluster_spinglass(g, gamma=1.5)
png("test2.png", pointsize=18, width=1200, height=1000)
par(mar=c(0,0,0,0))
set.seed(12345)
plot(g,
  vertex.size=14,
  vertex.label.color="black",
  vertex.color=communities$membership,
  vertex.label.cex=1.2,
  vertex.label.family="MEI",
  edge.color="black")
dev.off()