オプションという金融商品の理論価格を数値的に求める方法の1つに二項ツリーがあります。
二項ツリーの計算と表示を HTML と JavaScript で実装してみます。下の絵のようになります。

以下に何をやっているかの概要と HTML ソースを記します。厳密な議論は金融工学の本を、オプションの制度に関する正確な情報は取扱機関を参照してください。現実的な価格評価には目的に合う他の方法を用いてください。
まずオプションって何
「将来のある時点(まで)に、あらかじめ定められた価格で、原資産(何でもよいのですがここでは価格が時間変化するもの;典型的にはある会社の株)を購入 or 売却する権利を獲得する契約」★ のことをオプションといいます。あくまで購入 or 売却する権利を獲得する契約なので、購入や売却を必ず実行する必要はありません。
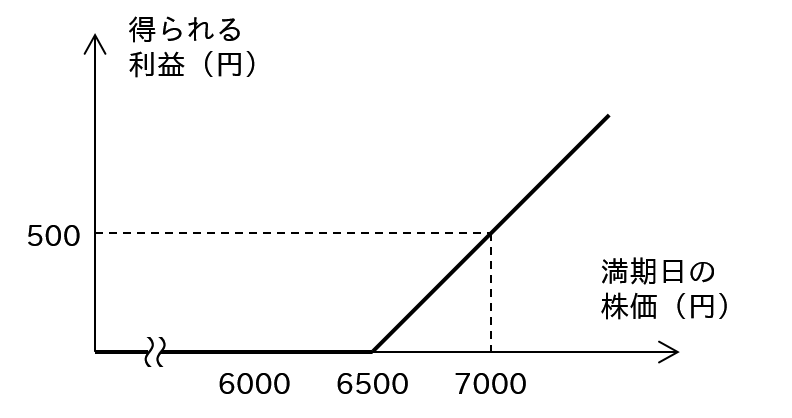
- 例えば、2017年9月にオプション契約により「2017年10月12日にX社株1株を6500円で購入する権利」を獲得したとして、
つまり、オプションによって獲得した権利は、2017年10月12日には確実に0円以上のお金になります(得られる利益は上図のようなランプ関数になり、株価がいくらになっても0以上になります)。「絶対に得をするか少なくとも損しない権利」をただでくれる人はいないので、通常オプション契約をするとき、権利を獲得する側がお金を払います(権利を得る方が、それに見合うお金を払います)。このときオプションの価格がいくらであれば得られる権利に見合っているのか、というのがこの記事の中心話題です。ちなみに、
- 「将来のある時点」のことをしばしば満期日といいます。
- 「あらかじめ定められた価格」のことをしばしば行使価格といいます。
- 原資産を購入する権利をもたらすオプションのことをコール、売却する権利をもたらすオプションのことをプットといいます。
- 満期日にのみ権利行使ができるオプションをヨーロピアン、満期日までの間いつでも権利行使ができるオプションをアメリカンといいます。地域の名前が付いていますがアメリカではオプションは全てアメリカン・オプションとかいうわけではありません。
- 満期日までの定められた複数時点で権利行使ができるバミューダン・オプションというのもあります。
- 日本の大阪取引所で取引されているオプションはすべてヨーロピアン・オプションです。
- もたらされる権利がもっと複雑なオプションをエキゾチック・オプションといいます(上の ★ の図式に当てはまりませんが、もう少し広く、満期日までの原資産の価格変化がある条件を満たした場合に利益が得られ、満たさない場合には何も得られないような権利もオプションといいます)。
以下、権利を獲得する契約を結ぶことを単に「オプションを買う」、獲得させる契約を結ぶことを「オプションを売る」といいます。
オプションはどこで誰が売っているの
金融商品を取り扱うことのできる(しかるべき登録をした)機関(銀行や証券会社など)が、例えばある会社に対して、独自に自由に定義したオプションを売ることがあります。それとは別に、取引所という機関が、いくつか定められた原資産・満期日・行使価格のコール/プットオプションについては売り買いを受け付けているので、そこで提示された価格で売り買いすることもできます(個人は取引所での取引に直接参加できませんので、証券会社などのブローカーを通して売買することになります)。
じゃあオプションの価格がいくらなら得られる権利に見合っているの
ここでオプションの価格がいくらだと適正なのかを考えてみます。オプションの権利がいくらかをいきなり考えるのは難しそうなので、まずはもっと容易に価格を考えられそうな権利からスタートして、ついでに金融工学でよく置かれる仮定を確認していきたいと思います。
- まず、「権利を買った人が権利を売った人からすぐに1000円もらえる権利」という権利の価格は1000円に決まります。ここで、ものの価格は「リスクを取ることなしに利益を得られる機会が存在しない」ように決まるという無裁定条件を仮定しています。もしこの権利の価格が999円だったら、「999円でこの権利を買い、権利を行使して相手から1000円をもらう」という手順で無リスクで利益を得ることができます。あるいはこの権利の価格が1001円だったら、「1001円でこの権利を売って、相手が権利行使してきたら1000円をあげる」という手順でやはり無リスクで利益を得ることができます。なので価格は必ず1000円でなければならないという考え方をします。
- 次に、「権利を買った人が権利を売った人から1年後に1000円もらえる権利」を考えてみると、こちらは1000円にはなりません。1年間お金を貸し出すときの無リスク金利を 2% とすると、 1000 / 1.02 = 980.3922 円がこの権利の適正な価格になります。無リスク金利とは絶対に返してくれる相手にお金を貸したときにもらえる金利です。ここで、無リスク金利で無リスクにお金を貸し借りできる相手の存在を仮定します。それで「1年後に1000円もらえる権利」がなぜ先のように決まるのかに戻ると、これもやはり無裁定条件によります。もし先の権利が990円ならば、「この権利を誰かに売却することで990円を手に入れ、無リスクなお金の貸し出し先にその990円を貸し出し、1年後に権利行使してきた相手に1000円を受け渡すが、貸し出した 990 円が 990 × 1.02 = 1009.8 円になって返ってくるので差し引き 9.8 円の利益」というシナリオで無リスクに利益を捻出できます。先の権利が970円ならば、「無リスク金利でお金を借り入れて970円を調達し、そのお金で権利を購入し、1年後に 970 × 1.02 = 989.4 円を返済するとともに、権利を行使して1000円受け取り、差し引き10.6円利益」というシナリオで無リスクに利益を捻出できます。ここで、0.6円などは現実にはやり取りできませんが、気にしないことにします。
- 最後に「権利を買った人が権利を売った人から、$T$ 年後に、その時点の株価 $S_T$ に依存した $f(S_T)$ 円もらえる権利」を考えます。統計に強い人なら、「$T$ 年後の株価 $S_T$ の取る確率分布を仮定すれば、$f(S_T)$ の期待値を求められるのでは」と考えるかもしれません。確かにそれで $f(S_T)$ の期待値は求められますが、期待値を求めても問題は解決しません。というのは、「確実に1000円もらえる権利」と「10%の確率で10000円もらえる権利」の理論価格は異なりうるからです。この場合の後者の理論価格は、実は個々人にとって異なり、個々人がどれだけリスクをとってもよいと考えるかに依存します。多くの人はリスクをとることをマイナス要素と考えるといわれているので、多くの人にとって後者は前者と期待値は同じだが前者よりリスクがある分1000円より安くなると考えられます。
- それでは「確率的な利益をもたらすオプションの理論価格は個々人のリスク選好によって異なってしまうので、権利に見合う価格かどうかは人それぞれになってしまうのではないか」というと、実はそのようなことになりません。というのは、オプションは確かに確実な利益ではなく確率的な利益をもたらすのですが、その確率分布は他の物の価格と独立ではないからです。つまり、株価に依存するからです。オプション価格が株価に依存するということは、株とオプションを適当な比率で組み合わせることで確率的な項を(少なくとも微小時間のあいだ)打ち消し、無リスクな資産にすることができることを意味します。無リスクな資産については、「無リスクに利益を得られる機会がないか」を厳しくチェックしなければなりません。
- そして、株も確率的な金融商品ですが、現在の株価は需要と供給のバランスによりただ1つに決まっています。すると、以下の手順でオプション価格を求めることができます。
- まず、株とオプションを組み合わせて無リスクな資産をつくります。
- 無裁定条件から無リスクなな資産のあるべき現在の理論価格を求めます。
- 無リスクな資産のうち株の部分については現在の株価から価格がわかっているので、それを差し引けばオプションの部分の価格が求まります。
それで結局オプション価格の求め方は、
微小時間で無裁定条件が成り立つとして、オプション価格の確率微分方程式を解く方法が問題に対しては一番素直といえます(仮定によっては解析的に解けます)。それとは別に、二項ツリーのように「微小時間ずつ枝を分岐させて枝上のシナリオに沿って解く」という数値的な解法もありえます。
以下に二項ツリーの計算例を示します(ノートPCの電池が切れそうなのでこちらの仮定や解説は後日気が向いたら…)。
HTMLソース
<html>
<head>
<title>二項ツリー</title>
<style type="text/css">
body { margin: 30px; font-family: メイリオ; font-size: 93%; color: #444444; line-height: 1.2; background: #fff8dc;}
input.style1 { font-family: メイリオ; font-size: 93%; color: #444444; text-align: right; }
table { border-collapse: collapse; }
td { padding: 0.2em; }
</style>
<script type="text/javascript">
// [STEP1] 二項ツリーを作成 (全てのノードにIDを付与し親子関係を整理)
function myCreateTree(step) {
// 例えば1期間二項ツリー (ノードは3個のみ) であればこの関数では以下のような配列を生成する
// [ [時点0, 上側の親はなし, 下側の親はなし, 上側の子は1番, 下側の子は2番],
// [時点1, 上側の親はなし, 下側の親は0番, 上側の子はなし, 下側の子はなし],
// [時点1, 上側の親は0番, 下側の親はなし, 上側の子はなし, 下側の子はなし]]
// 後から株価とオプション価格をさらに付け足す
var tree = [];
var id = 0;
for (var t = 0; t <= step; ++t) {
for (var i = 0; i < t+1; ++i) { // 時点tには t+1 個のノードが存在
tree.push([]);
tree[id].push(t); // このノードの時点
tree[id].push(NaN); // 上側の親のID (後で埋めるので仮にNaNとする)
tree[id].push(NaN); // 下側の親のID (後で埋めるので仮にNaNとする)
tree[id].push(t==step ? NaN : id + t + 1); // 上側の子のID
tree[id].push(t==step ? NaN : id + t + 2); // 下側の子のID
++id;
}
}
// 親のIDを書き入れる
for (var id = 0; id < tree.length; ++id) {
if (!isNaN(tree[id][3])) { // 上側の子がいるならその子にとって下側の親
tree[tree[id][3]][2] = id;
}
if (!isNaN(tree[id][4])) { // 下側の子がいるならその子にとって上側の親
tree[tree[id][4]][1] = id;
}
}
return tree;
}
// [STEP2] 二項ツリーに株価を書き入れる (根元から末端へ)
function myAddStockPrice(tree, S_0, u, d) {
tree[0].push(S_0);
for (var id = 1; id < tree.length; ++id) {
if (!isNaN(tree[id][2])) { // 下側の親がいる場合は下側の親を参照
tree[id].push(u * tree[tree[id][2]][5]);
} else if (!isNaN(tree[id][1])) { // 上側の親がいる場合は上側の親を参照
tree[id].push(d * tree[tree[id][1]][5]);
} else { // ERROR
tree[id].push(NaN);
}
}
return tree;
}
// [STEP3] 二項ツリーにオプション価格を書き入れる (末端から根元へ)
function myAddOptionPrice(tree, is_call, is_american, strike_price, p, a) {
// 末端のノードを先に記入
for (var id = 1; id < tree.length; ++id) {
if (isNaN(tree[id][3])) { // 上側の子がいない ⇔ 末端のノード
if (is_call) { // コールであれば行使価格 < 株価のときに利益、そうでないときはゼロ
tree[id].push(strike_price < tree[id][5] ? tree[id][5] - strike_price : 0);
} else { // プットであれば行使価格 < 株価のときに利益、そうでないときはゼロ
tree[id].push(tree[id][5] < strike_price ? strike_price - tree[id][5] : 0);
}
} else { // 末端ではない場合は仮に NaN とする
tree[id].push(NaN);
}
}
// 末端ではないノードを末端側から記入
for (var id = tree.length - 1; id >= 0; --id) {
if (!isNaN(tree[id][3])) {
var f = (p * tree[tree[id][3]][6] + (1.0-p) * tree[tree[id][4]][6]) / a;
if (is_american) { // アメリカンの場合期限前行使した方がよいかどうか確認
var f_early = is_call ? (strike_price < tree[id][5] ? tree[id][5] - strike_price : 0)
: (tree[id][5] < strike_price ? strike_price - tree[id][5] : 0);
tree[id][6] = Math.max(f, f_early);
} else {
tree[id][6] = f;
}
}
}
return tree;
}
function myAppendStockPrice(cell, price) { // 株価のセル
cell.appendChild(document.createTextNode(parseFloat(price).toFixed(3)));
cell.style.backgroundColor = "lightcyan";
cell.style.border = "2px solid #444444";
cell.style.borderBottom = "0";
cell.style.paddingTop = "0.3em";
cell.style.textAlign = "right";
}
function myAppendOptionPrice(cell, price) { // オプション価格のセル
cell.appendChild(document.createTextNode(parseFloat(price).toFixed(3)));
cell.style.backgroundColor = "paleturquoise";
cell.style.border = "2px solid #444444";
cell.style.borderTop = "0";
cell.style.paddingTop = "0.3em";
cell.style.textAlign = "right";
}
// ツリーの内容をHTMLテーブルにする
function myCreateTable(tree, step, interval) {
var table = document.createElement("table");
var rows = [];
for (var i = 0; i < 1 + 2 * (step + 1); ++i) {
rows.push(table.insertRow(-1));
if (i == 0) {
for (var j = 0; j <= step; ++j) {
var cell = rows[i].appendChild(document.createElement("th"));
cell.appendChild(document.createTextNode("t=" + parseFloat(j * interval).toFixed(3)));
cell.style.paddingBottom = "0.5em";
cell.style.textAlign = "center";
}
} else {
for (var j = 0; j <= step; ++j) {
rows[i].insertCell(-1);
}
}
}
var t_last = -1;
var i = 0;
for (var id = 0; id < tree.length; ++id) {
var t = tree[id][0];
if (t != t_last) {
i = 0;
t_last = t;
}
myAppendStockPrice(rows[1+step-t+2*i].cells[t], tree[id][5]);
myAppendOptionPrice(rows[1+step-t+2*i+1].cells[t], tree[id][6]);
++i;
}
rows[1+step-0+1].cells[0].style.fontWeight = "bold";
return table;
}
// 「オプション価格を計算」クリック時の処理
function myCalcOptionPrice() {
var S_0 = document.myForm.textStockPrice0.value;
var sigma = document.myForm.textVolatility.value;
var r = document.myForm.textRiskFreeRate.value;
var r_underlying = document.myForm.textYieldUnderlying.value;
var is_call = document.myForm.radioCallPut[0].checked;
var is_american = document.myForm.radioEuropeanAmerican[1].checked;
var strike_price = document.myForm.textStrikePrice.value;
var maturity = document.myForm.textMaturity.value;
var step = document.myForm.textStep.value;
var interval = maturity / step; // 1ステップの期間
var u = Math.exp(sigma * Math.sqrt(interval)); // ツリーの上昇幅 (倍)
var d = 1.0 / u; // ツリーの下降幅 (倍)
var a = Math.exp(r * interval); // 1期間あたりの無リスク利回り
var a_modified = Math.exp((r - r_underlying) * interval); // 原資産利回りがある場合の p 計算用修正版
var p = (a_modified - d) / (u - d); // リスク中立世界で株価が上昇する確率
// オプション価格を計算 (ツリーを作成 → 株価を書き入れ → オプション価格を書き入れ)
var tree = myCreateTree(step);
tree = myAddStockPrice(tree, S_0, u, d);
tree = myAddOptionPrice(tree, is_call, is_american, strike_price, p, a);
// ツリーの内容をHTMLテーブルにして表示
document.getElementById("outputArea").textContent = null;
document.getElementById("outputArea").appendChild(myCreateTable(tree, step, interval));
}
// 初期化
function mySet() {
document.myForm.textStockPrice0.value = 4050;
document.myForm.textStrikePrice.value = 4000;
document.myForm.textMaturity.value = 0.5;
document.myForm.textVolatility.value = 0.2;
document.myForm.textRiskFreeRate.value = 0.05;
document.myForm.textYieldUnderlying.value = 0.02;
document.myForm.textStep.value = 4;
myCalcOptionPrice();
}
</script>
</head>
<body onload="mySet()">
<form name="myForm">
<table style="float: left; margin-right: 1.0em;">
<tr>
<td colspan=2 style="padding: 0 0 0.5em 0;">
<input type="radio" name="radioCallPut" checked="checked"> コール</br>
<input type="radio" name="radioCallPut"> プット</td>
</tr>
<tr>
<td colspan=2 style="padding: 0 0 0.5em 0;">
<input type="radio" name="radioEuropeanAmerican" checked="checked"> ヨーロピアン</br>
<input type="radio" name="radioEuropeanAmerican"> アメリカン
</td>
</tr>
<tr>
<td>現在の株価 </td>
<td><input type="test" size="6" name="textStockPrice0" class="style1"></td>
</tr>
<tr>
<td>行使価格 </td>
<td><input type="test" size="6" name="textStrikePrice" class="style1"></td>
</tr>
<tr>
<td>満期 </td>
<td><input type="test" size="6" name="textMaturity" class="style1"></td>
</tr>
<tr>
<td>ボラティリティ </td>
<td><input type="test" size="6" name="textVolatility" class="style1"></td>
</tr>
<tr>
<td>無リスク金利 </td>
<td><input type="test" size="6" name="textRiskFreeRate" class="style1"></td>
</tr>
<tr>
<td>原資産利回り </td>
<td><input type="test" size="6" name="textYieldUnderlying" class="style1"></td>
</tr>
<tr>
<td>ツリーの期間数 </td>
<td><input type="test" size="6" name="textStep" class="style1"></td>
</tr>
<tr>
<td colspan=2 style="padding: 0.5em 0;"><input type="button" value="オプション価格を計算" onclick="myCalcOptionPrice()" class="style1" style="width: 215px; height: 50px; text-align: center;"></td>
</tr>
</table>
<div id="outputArea"></div>
</form>
</body>
</html>