はじめに
この記事では、Rで葉の多い回帰木を描画する際の工夫を記録しておきます。
使用するパッケージは決定木の計算でrpart、描画でpartykitを想定しています。
勉強のため、ご指摘等いただけると助かります。
(参考:partykitのドキュメント https://cran.r-project.org/web/packages/partykit/partykit.pdf)
動機
決定木で分析する際、木をある程度成長させたほうが良い示唆が得られることがあります。
過学習の問題とはうまく付き合う必要がありますが。
決定木の可視化を行うパッケージpartykitは、特に投入変数にカテゴリー変数が含まれる場合にとてもわかりやすいため、私はよく使っています。
ただ回帰木で葉が多いときの出力結果は、時折イマイチなことがあります。
探してもあまり良い記述がなかったため、ここに記録しておきます。
決定木の計算
ここではボストン市の住宅価格(Boston)を用います。
不動産価格を多くの投入変数から説明することを試みます。
データセットの中身は次のページがわかりやすく解説しています。
The Boston Housing Dataset
ライブラリ
library(MASS)
library(rpart)
library(partykit)
実行
>tree <- rpart(medv ~., data=Boston, method='anova')
>print(tree)
n= 506
node), split, n, deviance, yval
* denotes terminal node
1) root 506 42716.3000 22.53281
2) rm< 6.941 430 17317.3200 19.93372
4) lstat>=14.4 175 3373.2510 14.95600
8) crim>=6.99237 74 1085.9050 11.97838 *
9) crim< 6.99237 101 1150.5370 17.13762 *
5) lstat< 14.4 255 6632.2170 23.34980
10) dis>=1.5511 248 3658.3930 22.93629
20) rm< 6.543 193 1589.8140 21.65648 *
21) rm>=6.543 55 643.1691 27.42727 *
11) dis< 1.5511 7 1429.0200 38.00000 *
3) rm>=6.941 76 6059.4190 37.23816
6) rm< 7.437 46 1899.6120 32.11304
12) lstat>=9.65 7 432.9971 23.05714 *
13) lstat< 9.65 39 789.5123 33.73846 *
7) rm>=7.437 30 1098.8500 45.09667 *
決定木が得られました。
可視化
rpartでも可視化できますが、ここではpartykitを使用します。
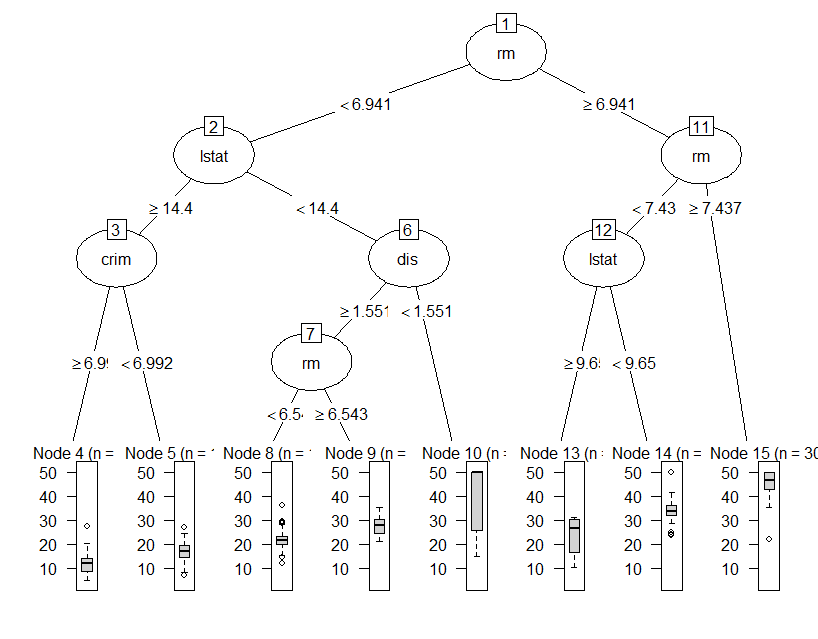
> plot(as.party(tree))
部屋数(rm)が多いほど価格が高いことがわかります。
この場合はbox chartでもわかりやすいです。
ただし実務上では、よりわかりやすく平均値を表示することがあります。
このためにplot関数にtype='simple'を渡します。
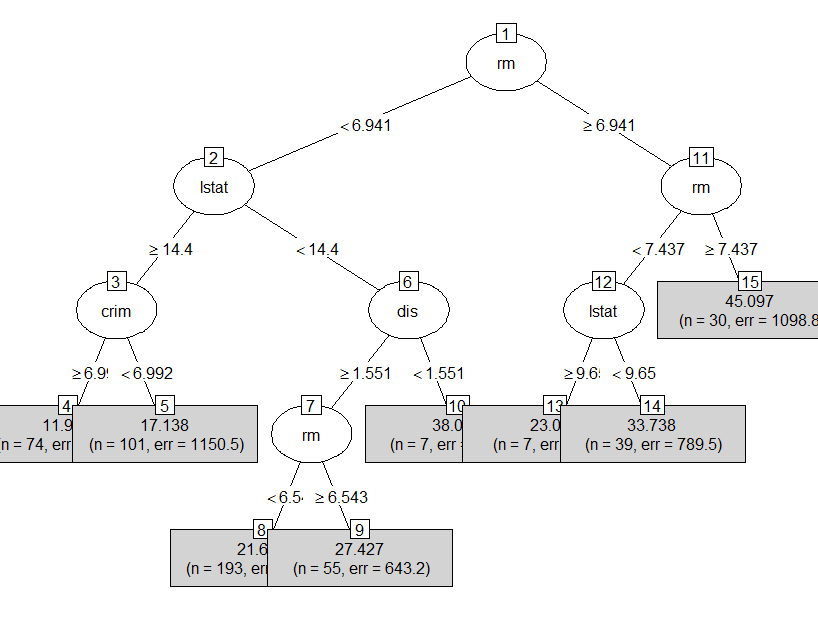
> plot(as.party(tree), type='simple')
重なって見づらくなってしまいました。。
葉を少なくすれば重なりは解消されますがここでは木をある程度成長させる場合を考えます。
修正
さきほどの葉の重なりを解消するため、葉に記載する情報を整理することを考えます。
まず有効数字は幅を取りすぎているため、減らします。
また誤差の出力をやめることでも、スペースを確保できそうです。
無視して良いということではありませんが。
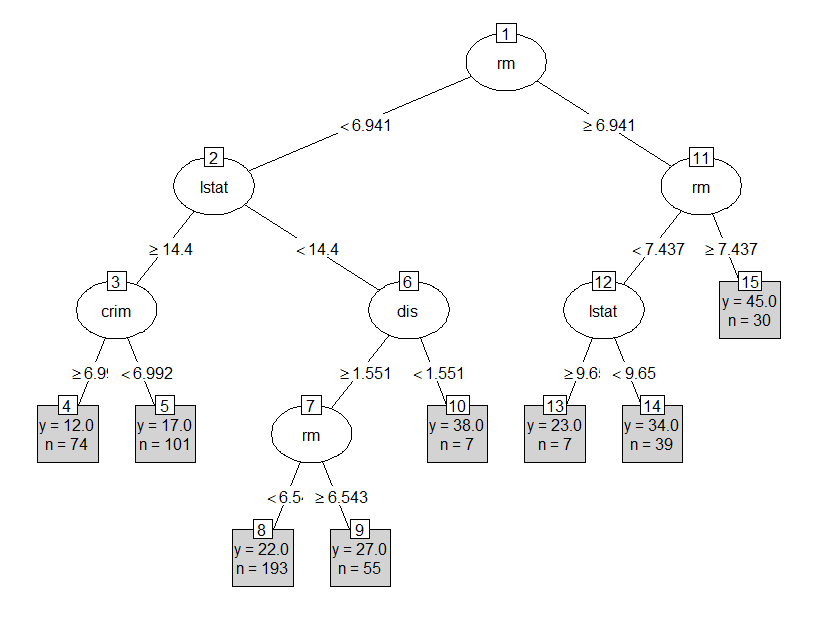
partykitのplotにおいて、tp_argsに値を渡すことで、ターミナルノードの出力を制御できます。
ここでは平均値とN数を、指定した桁数で、それぞれ y = , n = の形で返す関数を渡します。
plot(as.party(tree), type='simple',tp_args = list(FUN = function(info)
c(paste('y = ',format(round(info$prediction, digits=1), nsmall = 1), sep=''),
paste('n = ',format(round(info$n)), sep=''))
))
重なりは解消されました。葉同士の平均値の上下関係も見やすいです。
おわりに
決定木はとても便利ですが、この便利さは結果の解釈の簡単さに起因しています。
よりわかりやすく可視化すれば、自分が見つけた示唆がより他人に伝わると考えています。
より良い方法がありましたら、ご教授いただけると幸いです。