改訂履歴
2021.09.13 タイトル変更
1.今回の目的
はじめまして。Chimoと申します。
今回Qiitaに初めて記事を書いてみようと思います。
会社での調べものやE資格の勉強の際はいつもQiitaを除いており、皆様の記事に大変お世話になりました。
私ごときが投稿するのは非常に緊張しますが、頑張ります。
記事に関してご意見やご感想ございましたら、勉強になりますのでコメントいただけますと幸いです。
さて、今回は記事を書く練習を兼ね、Boston Housingのデータセットを用いて
住宅価格の線形回帰モデルを作ることを目標にしたいと思います。
2.データセット読み込み「Boston Housing」
scikit-learnに付属するデータセットから、Boston Housingを読み込みます。
import numpy as np
import matplotlib.pyplot as plt
# %matplotlib inline で アウトプット行にグラフを表示できる様になるらしい
%matplotlib inline
from sklearn.datasets import load_boston
以下の様に変数XとYに読み込ませます。
boston = load_boston()
X=boston.data #各特徴量
Y=boston.target #目的変数
fname=boston.feature_names #各特徴量の名称
X,Y,fnameのデータを取り出すと、ちゃんとデータが入っていることが確認できます。
X[:,1] #スライスで0行目を表示
(結果)
array([ 18. , 0. , 0. , 0. , 0. , 0. , 12.5, 12.5, 12.5,
12.5, 12.5, 12.5, 12.5, 0. , 0. , 0. , 0. , 0. ,
~中略~
0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. , 0. ,
0. , 0. ])
Y[:5] #0~4個目までの要素を表示
(結果)
array([24. , 21.6, 34.7, 33.4, 36.2])
fname #各特徴量の名前
(結果)
array(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype='<U7')
3.関数作成
3.1 散布図表示
以下の通り散布図を表示させるための関数を作成します。
def plotdata(X,Y,num):
plt.xlabel(fname[num],fontsize=14)
plt.ylabel('住宅価格[千ドル]',fontsize=14,fontname="MS Gothic")
plt.title(fname[num] + 'と住宅価格[千ドル]の関係',fontsize=14,fontname="MS Gothic")
plt.scatter(X,Y,c='b')
plt.draw()
return
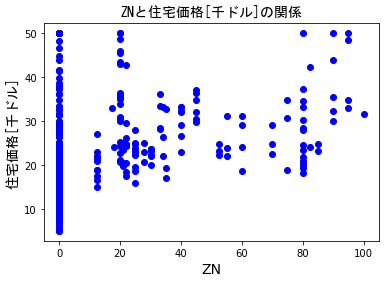
作った関数で"ZN"(*0)と価格の散布図を表示させると以下の通りです。
plotdata(X[:,1],Y,1)
(*0)ZNは25,000 平方フィート以上の住居区画の占める割合
3.2 仮説
次の式で仮説:h(線形回帰モデル)を定義します。
h = X * a + b
ここでXは入力データ,a,bはパラメータを示します。
def h(X,a,b):
h = X * a + b
return h
3.3 目的関数
以下の通り目的関数:Jを実装します。(数式の載せ方がわからない・・w)
def J(h,Y):
m = Y.size
J = np.sum(( h - y )**2) / (2*m)
return J
4.線形回帰の学習
4.1 用いる特徴量
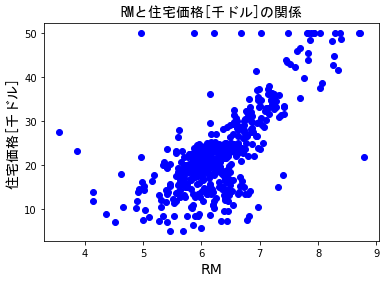
13個の特徴量を散布図で見ると"RM"(*1)が住宅価格と相関してそうなので,
適当ですが特徴量はこちらを選ぶことにします。
plotdata(X[:,5],Y,5)
4.2 学習の実施
3で作成した仮説と目的関数の関数を用いて,最急降下法によりパラメータa,bを学習させます。
ここで再急降下法は目的関数Jを各パラメータで偏微分して求めます(数式の載せ方がry)。
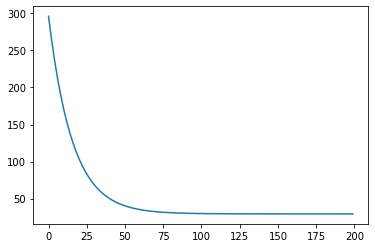
結果から,学習したパラメータa,bと,コスト関数の下がり具合を示したグラフが得られます。
グラフによると,100~125回くらい学習すれば十分な様ですね。
m = X.size
c = [] #costの累計に用いる配列をクリア
alpha = 0.01 #学習率
a = 0 #パラメータを初期化
b = 0
for i in range(200): #200回学習
H = h(X[:,5], a, b) #仮説にRM,パラメータ初期値を代入
J = j(H,Y) #目的関数の値を計算
c.append( J )#目的関数の値を累計
a = a - alpha * np.sum(( H - Y) * X[:,5]) / m # 最急降下法によりパラメータを学習
b = b - alpha * np.sum( H - Y) / m
plt.plot(c[0:200])#目的関数の値の類型をプロット
print('パラメータa:',a)
print('パラメータb:',b)
(結果)
パラメータa: 3.567989796463954
パラメータb: 0.4941873961329116
5.学習結果のプロットと考察
5.1 学習結果のプロット
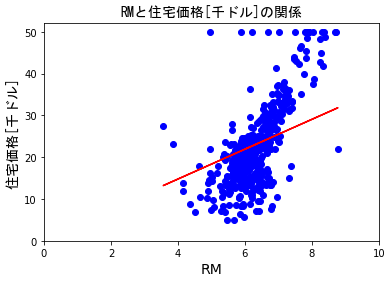
4.2にて学習した仮説h_resultをRMの散布図上に重ねてみます。
h_result = a * X[:,5] + b
plotdata(X[:,5],Y,5)
plt.xlim([0,10])
plt.ylim([0,52])
plt.plot(X[:,5],h_result, c='red')
学習回数を10→20→・・・90→100→200(おまけ)に連れ、仮説h_resultは以下gifの様にうごきました。
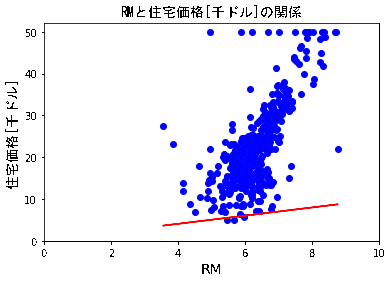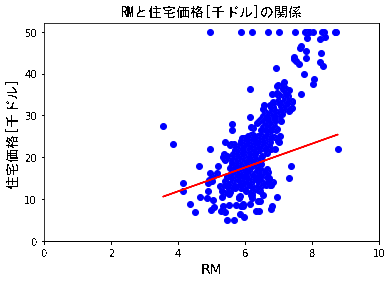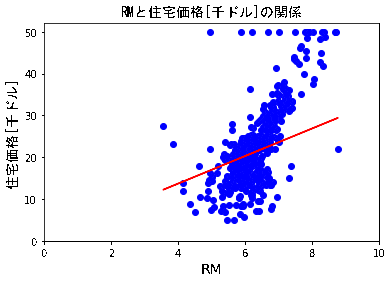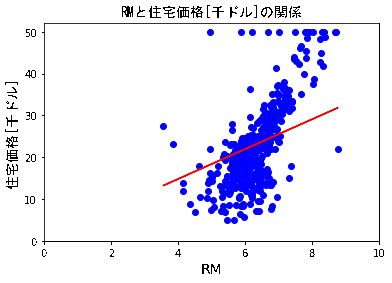
5.2 考察
RMのプロットに対し、感覚的にはh_resultの傾きはもう少しきつい方がよさそうに思えます。
学習データの前処理を行わずに学習させたので、外れ値の影響を受けているものと推測しています。
6.感想
初めて記事を書いてみましたが、とても楽しかったです。
数式の載せ方については調べておきたく思います・・・
次回以降でRMの前処理後の回帰や住宅価格の予測,重回帰等にも挑戦してみたいと思います。
以 上