実務でよく使うPyTorchの機能まとめ④｜パラメータ処理(torch.nn.Linear)

torch.nn.Linear

PyTorchで線型回帰の演算を行う場合はtorch.nn.Linearクラスを用いると良いです。torch.nn.Linearクラスは下記のように用いることができます。

import torch

linear1 = torch.nn.Linear(10, 20)
x1 = torch.randn(128, 10)
x2 = torch.randn(128, 25, 10)
output1 = linear1(x1)
output2 = linear1(x2)

print(type(x1))
print(x1.shape)
print(type(linear1))
print(linear1)
print(linear1.weight.shape)
print(linear1.bias.shape)
print(linear1.bias)
print(type(output1))
print(output1.shape)
print(x2.shape)
print(output2.shape)

・実行結果

<class 'torch.Tensor'>
torch.Size([128, 10])
<class 'torch.nn.modules.linear.Linear'>
Linear(in_features=10, out_features=20, bias=True)
torch.Size([20, 10])
torch.Size([20])
Parameter containing:
tensor([ 0.2451, -0.2494,  0.0917, -0.2745,  0.0626,  0.0891,  0.1838, -0.0752,
         0.2727, -0.2957,  0.2192,  0.2611, -0.0357, -0.0109,  0.0869,  0.2544,
         0.2898, -0.2472, -0.2130,  0.1839], requires_grad=True)
<class 'torch.Tensor'>
torch.Size([128, 20])
torch.Size([128, 25, 10])
torch.Size([128, 25, 20])

実行結果より、$128 \times 10$の入力(x)にlinear1 = torch.nn.Linear(10, 20)によって定義されたlinear1を作用させることで、$128 \times 20$の出力(output)が得られることが確認できます。ここで特に抑えておくと良いのがtorch.nn.Linearで作成されたlinear1オブジェクトからlinear1.parametersやlinear1.biasを用いることでパラメータを抽出することができるということです。

https://pytorch.org/docs/stable/generated/torch.nn.Linear.html

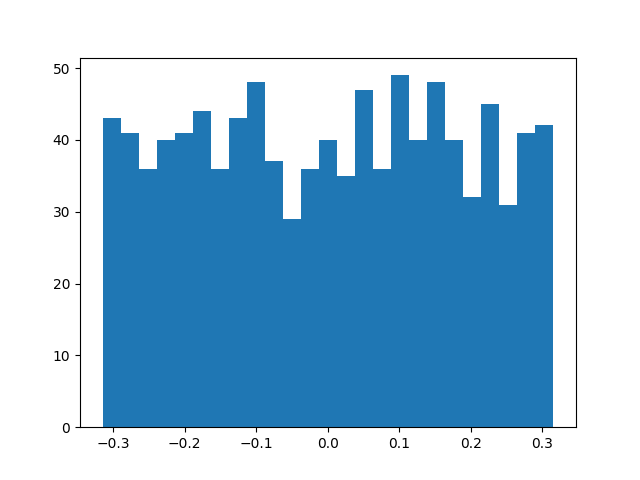
また、linear1.parametersやlinear1.biasの初期値の生成については上記を詳しく確認しておくと良いです。たとえばtorch.nn.Linear(10, 20)の場合のパラメータの値の分布のヒストグラムは下記を実行することで作成することができます。

import matplotlib.pyplot as plt
import torch
torch.manual_seed(10)

linear1 = torch.nn.Linear(10, 100)

plt.hist(linear1.weight.view(-1,1).detach().numpy(), bins=25)
plt.savefig("hist_Linear_init1.png")

・実行結果

$\sqrt{k} = 1/\sqrt{10} = 0.316 \cdots$であるので、$U(-\sqrt{k}, \sqrt{k})$に基づいて初期値のサンプリングが生成されていることが確認できます。また、結果に再現性を持たせるにあたってtorch.manual_seed(10)を追記しました。

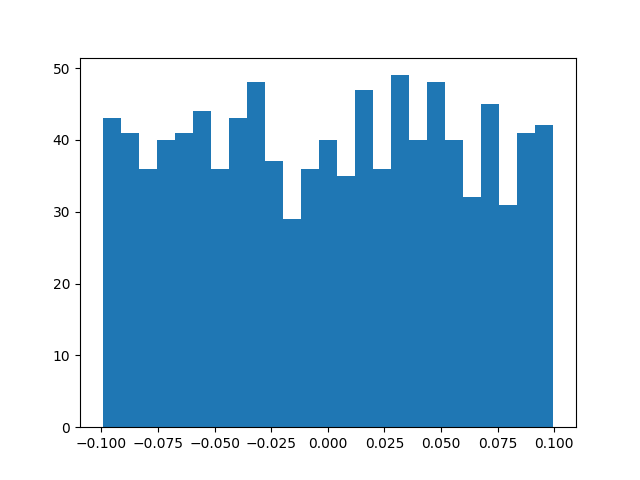
$k = 1/\sqrt{\mathrm{infeatures}}$であるので、以下ではin_features=100の場合でも同様なコードで確認を行いました。

import matplotlib.pyplot as plt
import torch
torch.manual_seed(10)

linear1 = torch.nn.Linear(100, 10)

plt.hist(linear1.weight.view(-1,1).detach().numpy(), bins=25)
plt.savefig("hist_Linear_init2.png")

・実行結果

実行結果を確認すると、$k = 1/\sqrt{\mathrm{infeatures}} = 0.1$でサンプリングが行われていることが確認できます。