UMAPの論文の確認
UMAPの論文は難しいので以下ではUMAPの論文のSection.3(A Computational View of UMAP)を中心に確認します。
UMAPの概要
UMAPはt-SNEやLargeVis、その他多くの次元の削減手法と同様に下記のような手順で実現されると解釈することができます。
1. Graph Construction
2. Graph Layout
1.のGraph Constructionは高次元の特徴量を元にkNN(k-Nearest Neighbor)法などを用いてサンプルをノードと見なしたグラフ(隣接行列)を生成する処理に対応します。また、2.のGraph Layoutは1.で作成した隣接行列を元に隣接するサンプルが近くなるように低次元に配置する処理です。
t-SNEやLargeVisについては下記で詳しく取り扱ったので当記事と合わせてご確認ください。t-SNEについてはt-SNEの論文ではグラフ的な処理で記述されていない一方で、処理自体はグラフで表せるのでt-SNEもGraph ConstructionとGraph Layoutに基づいて理解することが可能です。
Graph Construction
入力サンプルの集合を$X={x_1, \cdots x_N }$、$x_i$のk近傍の集合を${ x_{i_1}, \cdots x_{i_k} }$、metricを$d: X \times X \to \mathbb{R}_{\geq 0}$とするとき、それぞれの$x_i$について$\rho_i$と$\sigma_i$を下記の式に基づいて定義します。
\begin{align}
\rho_i = \min{ \{d(x_i, x_{i_j}) | 1 \leq j \leq k, d(x_i, x_{i_j}) > 0 \} } \\
\sum_{j=1}^{k} \exp{\left( \frac{-\max{(0, d(x_i, x_{i_j})-\rho_i}}{\sigma_i} \right)} = \log_{2}(k)
\end{align}
Graph Constructionではサンプルをノードと見なす重み付きグラフ$\bar{G} = (V, E, W)$の構築を行います。重み行列(2値の隣接行列の拡張ともみなせる)の$W$の$(i, i_j)$成分$W(x_i, x_{i_j})$は上記で定義した$\rho_i$と$\sigma_i$を元に下記のような式で定義されます。
W(x_i, x_{i_j}) = \exp{\left[ \frac{-\max{(0, d(x_i, x_{i_j})-\rho_i}}{\sigma_i} \right]}
ここで重み付き隣接行列$A$は重み行列の$W$を用いて下記のように定義されます。
A = A + W^{\mathrm{T}} - A \circ A^{\mathrm{T}}
Graph Layout
以下では低次元空間におけるforce directed graph layout algorithmについて確認します。force directed graph layout algorithmでは前項のGraph Constructionで構築したグラフのエッジに基づいて計算するノード間の引力(attractive force)と全てのノード間に生じる斥力(repulsive force)の平衡によって低次元空間におけるサンプルの位置を計算します。引力と斥力の平衡状態を作り出すにあたっては繰り返し演算(The algorithm proceeds by iteratively applying attractive and repulsive forces at each edge or vertex.)が実行されます。
ノード$i$とノード$j$の低次元空間における位置を$\mathbf{y}_i$、$\mathbf{y}_j$とおくとき、UMAPではノード間の引力$f_a$が下記のように定義されます。
f_a = \frac{-2ab ||\mathbf{y}_i - \mathbf{y}_j||_{2}^{2(b-1)}}{1 + ||\mathbf{y}_i - \mathbf{y}_j||_{2}^{2}} w(x_i, x_j)(\mathbf{y}_i - \mathbf{y}_j)
上記の数式の$a, b$はハイパーパラメータ(hyper parameter)です。同様にノード間の斥力$f_r$は下記のように定義されます。
f_r = \frac{2b}{(\epsilon + ||\mathbf{y}_i - \mathbf{y}_j||_{2}^{2})(\epsilon + a ||\mathbf{y}_i - \mathbf{y}_j||_{2}^{2b})} (1-w(x_i, x_j)(\mathbf{y}_i - \mathbf{y}_j))
上記の$\epsilon$は$0$での割り算を回避するにあたって用いられる0に近い正の数(small number)で$0.001$などが用いられます。
このように定義された引力と斥力を用いることでUMAPでは低次元空間における位置ベクトルを計算します。
UMAPの実装
UMAPのライブラリの概要とインストール
上記がUMAPのライブラリのドキュメントです。UMAPのインストールは下記を実行することでPyPIから入手することが可能です。
$ pip install umap-learn
UMAPライブラリを用いた次元削減については次項以降で確認します。
UMAPの基本処理と可視化
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, cross_val_score
from sklearn.neighbors import KNeighborsClassifier
import umap
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme()
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data,
iris.target,
stratify=iris.target,
random_state=42)
print(X_train.shape, y_train)
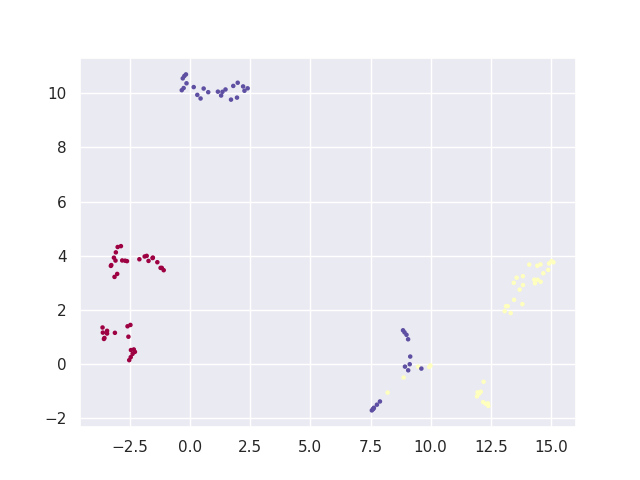
trans = umap.UMAP(n_neighbors=5, random_state=42).fit(X_train)
plt.scatter(trans.embedding_[:, 0], trans.embedding_[:, 1], s=5, c=y_train, cmap='Spectral')
plt.savefig("iris_UMAP1.png")
plt.close()
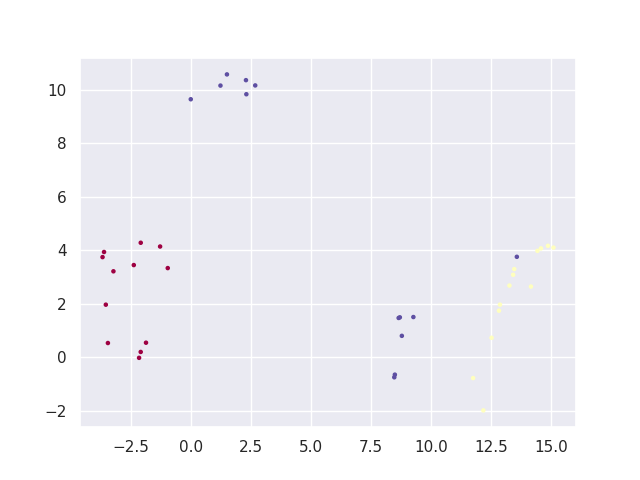
学習した関数の新規データへの適用
test_embedding = trans.transform(X_test)
plt.scatter(test_embedding[:, 0], test_embedding[:, 1], s= 5, c=y_test, cmap='Spectral')
plt.savefig("iris_UMAP2.png")