【論文まとめ】SIFT(Scale Invariant Feature Transform)

特徴点の抽出(Keypoints Detection)

DoG(Difference of Gaussians)の極値

\begin{align}
L(x, y, \sigma) &= G(x, y, \sigma) * I(x,y) \\
  &= \int \int G(x+u, y+v, \sigma) I(x+u,y+v) du dv \\
G(x, y, \sigma) &= \frac{1}{2 \pi \sigma^{2}} e^{-\frac{x^{2}+y^{2}}{2 \sigma^{2}}}
\end{align}

上記の式を元にDoG(Difference of Gaussians)の$D(x, y, \sigma)$は下記のように定義されます。

\begin{align}
D(x, y, \sigma) &= (G(x, y, \sigma) - G(x, y, \sigma)) + I(x,y) \\
  &= L(x, y, k \sigma) - L(x, y, \sigma)
\end{align}

DoG(Difference of Gaussians)の$D(x, y, \sigma)$の$D$は、「スケールの異なるガウシアンフィルタの適用結果の差が大きい点が特徴点であると判断する指標」と解釈すると良いです。

SIFT論文 Figure.2

実際の処理でDoGを用いて特徴点抽出を行うにあたっては上図のようにDoGが局所的に大きい(maxima)/小さい(minima)点を探すという処理が用いられます。図では近傍の26個のピクセルの値よりもDoGが大きい/小さい点を抜き出す処理に対応します。

Eliminating edge responses

SIFTのアルゴリズムでは前項のDoGに基づいて抽出した特徴点の候補に対しHarris Corner法に類似する方法を用いることでエッジの除去を行います。Harris Corner法については下記でまとめましたので下記をご確認ください。

SIFTの論文では前項で計算したDoG(Difference of Gaussian)の値を元に下記のようなヘッセ行列(Hessian Matrix)を計算します。

\begin{align}
H = \left(\begin{array}{cc} D_{xx} & D_{xy} \\ D_{yx} & D_{yy} \end{array} \right) 
\end{align}

上記のヘッセ行列の固有値の値に基づいて曲率(curvature)を計算できる一方で、固有値の計算にコストがかかることからSIFTではHarris Cornerと同様に固有値の計算を行わないで特徴点候補からのエッジの除去(eliminating edge)を行います。

\begin{align}
\mathrm{Tr}(H) &= D_{xx} + D_{yy} = \alpha + \beta \\
\mathrm{Det}(H) &= D_{xx} D_{yy} - (D_{xy})^{2} = \alpha \beta
\end{align}

ここで固有値の比を確認するにあたって$\alpha = r \beta$が成立するように$r$を定義すると、上記の式が成立することに基づいて下記のような式変形を行うことが可能になります。

\begin{align}
\frac{\mathrm{Tr}(H)^{2}}{\mathrm{Det}(H)} &= \frac{(\alpha + \beta)^{2}}{\alpha \beta} \\
  &= \frac{(r \beta + \beta)^{2}}{r \beta^{2}} \\
  &= \frac{(r+1)^{2}}{r}
\end{align}

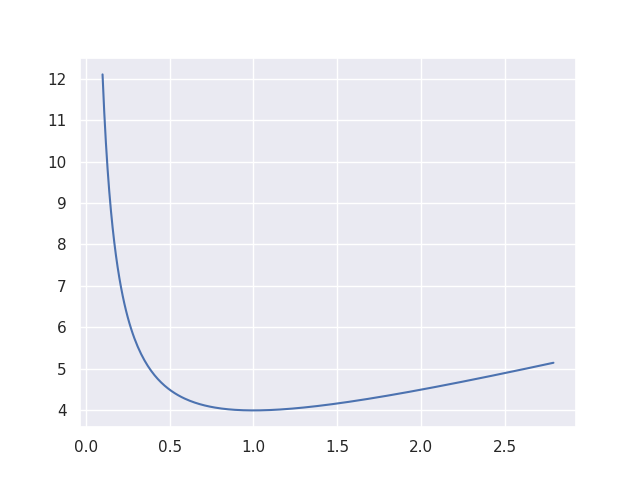
$r$の値を変化させながら上記の指標を図式化すると下記のような図が得られます。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_theme()

x = np.arange(0.1, 2.8, 0.01)
y = (x+1)**2/x

plt.plot(x, y)
plt.show()

plt.savefig("SIFT1.png")

・実行結果

実行結果の上図より、$\displaystyle \frac{\mathrm{Tr}(H)^{2}}{\mathrm{Det}(H)}$は$r=1, \alpha=\beta$すなわち固有値が一致する際に最小値を取ることが確認できます。このことに基づいてSIFTの論文では$r=10$すなわち指標が$11^2/10=12.1$を上回るとき特徴点ではなくエッジと判断して特徴点から取り除きます。$\mathrm{Tr}(H) = \alpha + \beta, \mathrm{Det}(H) = \alpha \beta$の導出については下記で取り扱ったので合わせてご確認ください。

特徴量の抽出

\begin{align}
m(x,y) &= \sqrt{ (L(x+1,y)-L(x-1,y))^{2} + (L(x,y+1)-L(x,y-1))^{2} } \\
\theta(x,y) &= \tan{\left[ \frac{L(x,y+1)-L(x,y-1)}{L(x+1,y)-L(x-1,y)} \right]}
\end{align}

SIFTのアルゴリズムでは前節で取り扱った特徴点抽出アルゴリズムの処理結果に対し、上記で定義される方向(角度$\theta$)のヒストグラムを大きさ$m$の重み付きで作成することで特徴量の抽出を行います。

SIFT論文 Figure.7