##やりたいこと
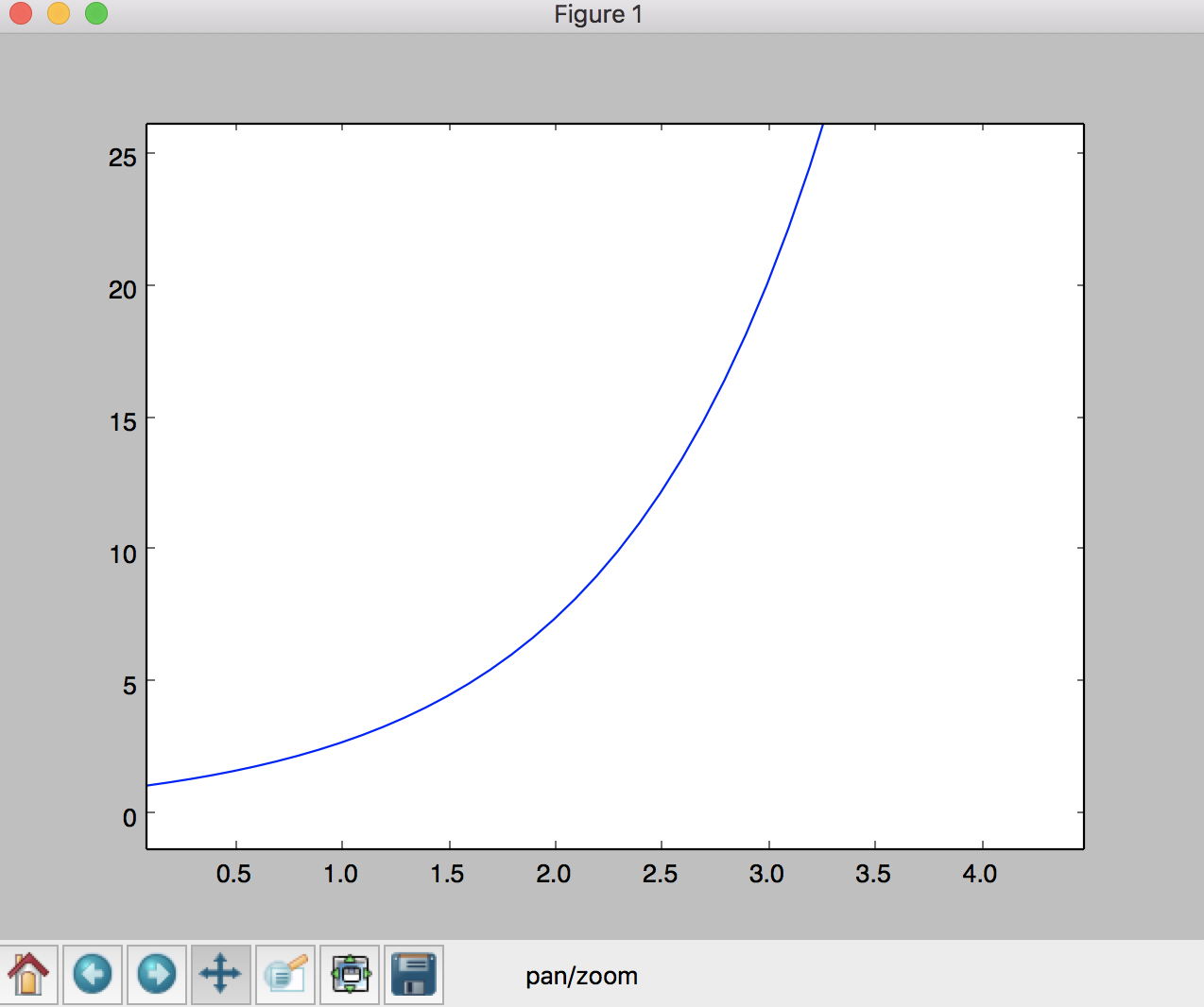
指数関数をグラフにプロットする
※準備するものは以下のURLを参照してください。
https://qiita.com/Cesaroshun/items/69c9fad0cd24322559b2
##ネイピア数とは
高校数学に出てくる自然対数の底ですね。
具体的には以下のような数字を示します。
e = 2.71828 18284 59045 23536 02874 71352 …
ちなみに僕の大学の研究室の暗証番号がこのネイピア数から、2718でした。数学科は気持ち悪いですね！！
##Pythonにおけるネイピア数の使い方
ネイピア数を用いて以下の数式を表現することができます。
\lim_{n \to \infty} (1 - \frac{1}{n})^n = \frac{1}{e} ≒0.367879⋯
確率的に考えると、当たる確率が1/nの宝くじを引くとします。
また、引いたくじは戻すというルールです。
上の式はn回くじを引いて、外れる確率を表しています。
それで行くと、1回で外れる確率はもちろん0%
(1 - 1)^1 = 0
nを限りなく大きくして行くと、外れる確率は期待値に反して少しずつ高まっていき、0.367879⋯に収束して行くことがわかっています。これを以下のように考えようというのがネイピア数の一部の考え方です。
\frac{1}{e} ≒0.367879⋯
よって、1/nの確率で当たるくじも、無限に引いていったら外れる確率はおよそ37%です。
こんな感じで、機械学習に応用していると思います。（まだ機械学習の実装はしたことない）
##手順
- ネイピア数を使うために、mathパッケージをインストール
- ネイピア数を定義
- グラフプロット実行
##まとめて結論
以下の記述を行う。
math_training.py
import matplotlib.pyplot as plt
import numpy as np
import math
x = np.arange(0, 10, 0.1)
/*mathパッケージでe(ネイピア数)を定義*/
e = math.e
y = e**x
plt.plot(x, y)
plt.show()
以下のグラフが出力される
x=0でy=1が確認できました。