1.パーセプトロンの学習規則
パーセプトロンの学習規則とは,線形識別関数の重みを学習によって求める方法である.パターンは,特徴空間上の一点で表現される.例えば,2クラスで考えた場合に,特徴空間上に分布している点を,線形識別関数によって生成される超平面によって,2つに分離できないかという話である.2つに分離するためには,線形識別関数の重みを調整しなければならない.その調整が学習となる.つまり,2つに分離するための超平面を,学習によって作り出す.
まず,クラスをCi(i=1...c),xを入力パターン,次元数をdとする.クラスCiの線形識別関数gi(x)は,
g_i(x) = ω₀+\sum_{j=1}^{d} ω_jx_j
今回は,簡略化のため2クラスで考える,クラスをC₁,C₂とする.また,gi(x)が最大であるとき,xの属するクラスはCiだと仮定する(線形識別関数によっては,最小が識別結果にもなり得るので,ここでは最大が識別結果になることを前置きした).
このとき,入力パターンがクラスC₁のとき,g₁(x)>g₂(x)である.そして,入力パターンがクラスC₂のとき,g₁(x)<g₂(x)である.
よって,識別関数gi(x)を1つにまとめて,
g(x) = g_1(x)-g_2(x)
=ω'₀+\sum_{j=1}^{d} ω'_jx'_j
※g(x)>0のとき,x∊C₁.g(x)<0のとき,x∊C₂
とした.
このg(x)におけるωが重みであり,この重みを最適な値にすることが学習の目的である.
以下の手順で,重みは求める.(ω'₀, ω'₁,...,ω'd)を重みベクトルWと表現する.
①まず,重みを適当に設定する
②学習パターンを選ぶ.(学習パターンとは,特徴ベクトルxとxが属するクラスCiの組)
③x∊C₁がg(x)<0のとき,重みベクトルWに学習パターンx(特徴ベクトル)に学習係数p掛けた値を足す.
x∊C₂がg(x)>0のとき,重みベクトルWに学習パターンx(特徴ベクトル)に学習係数p掛けた値を引く.
④手順②,③を全ての学習パターンに行う.
⑤全ての学習パターンで正しい識別結果が得られたら終了.1つでも誤りがあれば手順②に戻る.
このようにして重みベクトルWが得られる.これをg(x)に代入した線形識別関数は,特徴空間を超平面によってクラスごとに分離する.ただし,線形分離可能な分布に限る,なぜなら,パーセプトロンの学習規則は,線形分離可能である場合に,重みが収束するからである(パーセプトロンの収束定理).
2.Pythonで実装
まず,学習パターンの特徴ベクトルは,実行側の入力としても良かったが,線形識別可能な分布でないと,パーセプトロンの学習規則を適用できないので,あらかじめ設定しておいた.以下の通りである.
クラスC₁:x₁=(1,1,1,1),x₂=(1,0,1,1),x₃=(1,1,0,1),x₄=(1,1,1,0)
クラスC₂:x₅=(1,0,0,0),x₆=(1,1,0,0),x₇=(1,0,1,0),x₈=(1,0,0,1)
各特徴ベクトルの0番目の要素は全て1となっているが,これは線形識別関数g(x)のω₀に掛けてある値である.実質,1番目の要素以降の3つが特徴ベクトルであり,特徴空間も3次元である(厳密に言えば,1番目の要素を含んだ4次元のベクトルを拡張特徴ベクトルという.本来,特徴ベクトル(拡張が付かない)とは1番目からd番目までのベクトルを言う).3次元の特徴空間なので,2次元の超平面によって2つのクラスが分離されれば成功である.また,学習規則における学習係数は1とした.
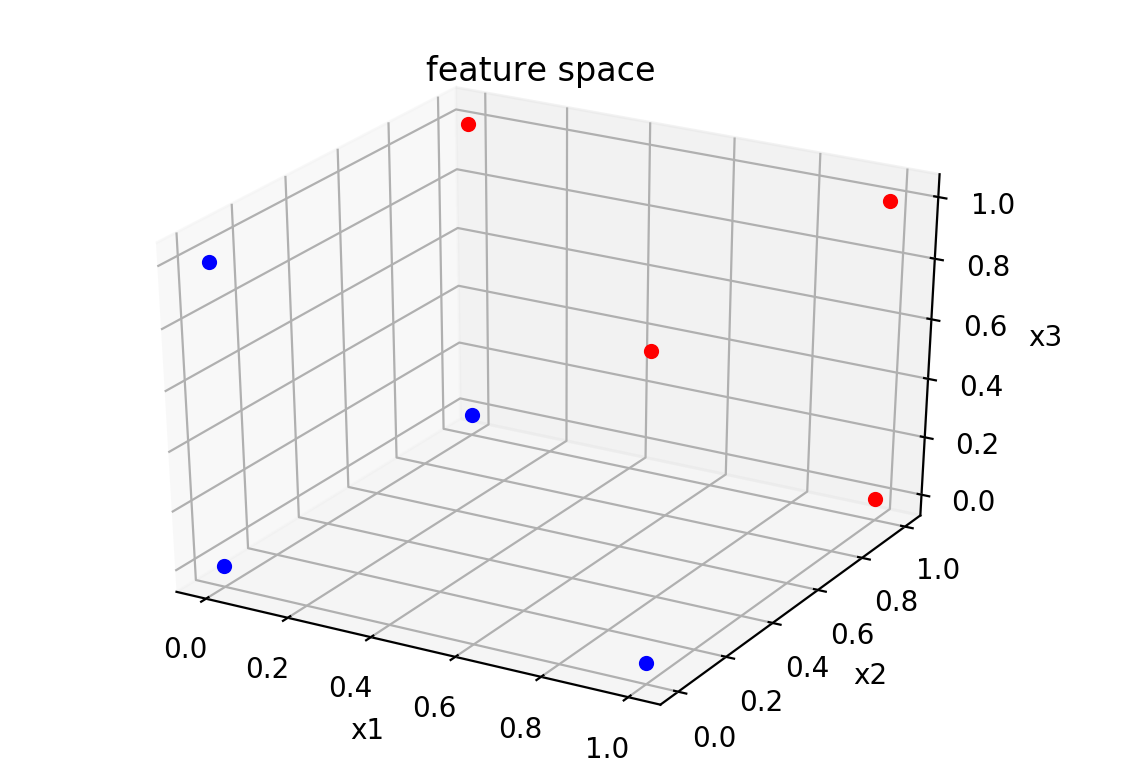
まずは,学習パターンの特徴ベクトルは以下のように特徴空間に分布している.
(赤:クラスC₁,青:クラスC₂)
学習規則をPythonで実装した.コードは以下の通りである.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# 学習パターンの特徴ベクトル
x = np.array([[1, 1, 1, 1], [1, 0, 1, 1], [1, 1, 0, 1], [1, 1, 1, 0], [1, 0, 0, 0], [1, 1, 0, 0], [1, 0, 1, 0], [1, 0, 0, 1]])
# 重みベクトル
w = np.array([-5, 1, 1, 1])
# パーセプトロンの学習規則
while True:
judge = 0
count = 1;
for data in x:
print(w)
if count <= x.shape[0]/2:
if np.dot(data, w)<=0:
w += data
judge = 1
else:
if np.dot(data, w)>=0:
w -= data
judge = 1
count += 1
print()
if judge == 0:
break
# 線形識別関数
def f(x1, x2):
return (w[1]*x1+w[2]*x2+w[0])/(-w[3])
x1, x2 = np.mgrid[-1:2:0.1, -1:2:0.1]
x3 = f(x1, x2)
# 特徴空間の設定
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d", facecolor="w")
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('x3')
ax.set_title("feature space")
# 線形識別関数の描画
ax.plot_surface(x1, x2, x3, cmap='BuGn')
i = 1
# 学習パターンの描画
for point in x:
if i<=x.shape[0]/2:
ax.scatter(point[1], point[2], point[3], c='red')
else:
ax.scatter(point[1], point[2], point[3], c='blue')
i += 1
# 特徴空間を表示
plt.show()
実行した結果,特徴空間は以下のようになった.
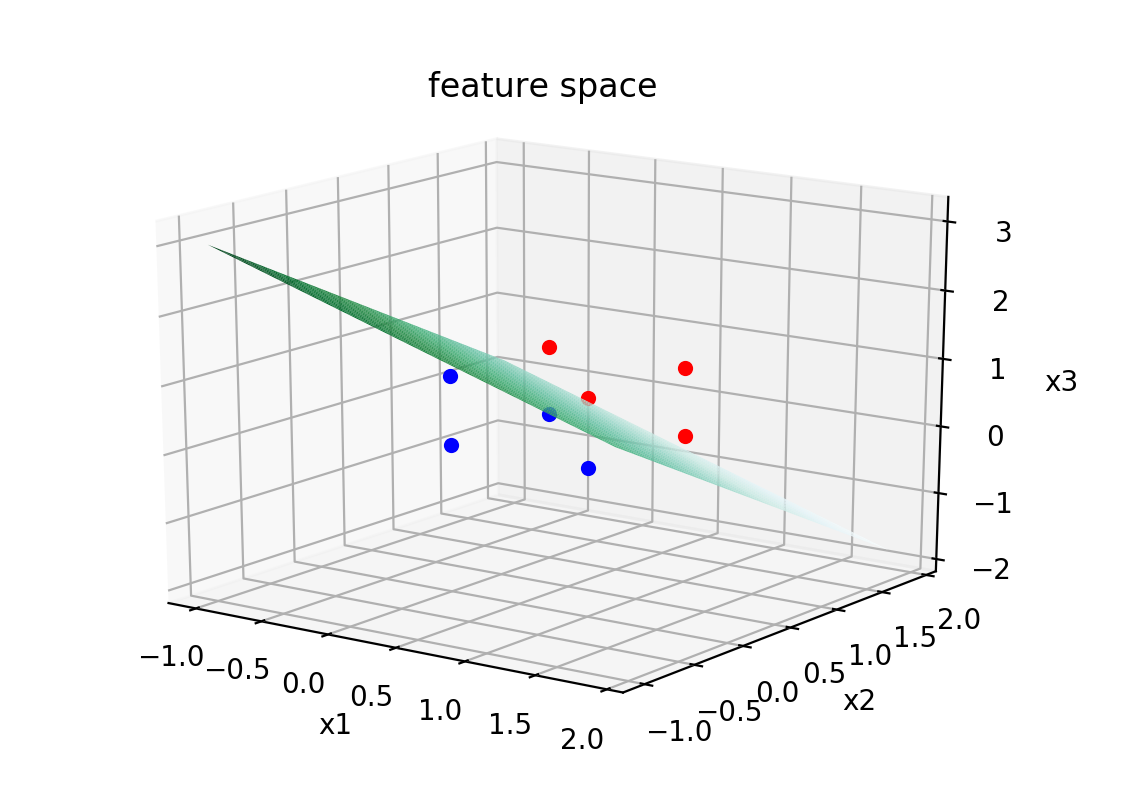
上図のように,赤と青の点が緑色の面(超平面)によって,分離されている.よって,学習規則で重みが求まったことがわかる.
3.参考文献
[1]石井健一郎,上田修功,前田英作,村瀬洋.「わかりやすいパターン認識 第2版」.オーム社,2019.